2022-2023学年浙教版九年级数学上册3.8弧长及扇形的面积选择专项练习题(含答案)
文档属性
| 名称 | 2022-2023学年浙教版九年级数学上册3.8弧长及扇形的面积选择专项练习题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 298.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 21:15:26 | ||
图片预览



文档简介
2022-2023学年浙教版九年级数学上册《3.8弧长及扇形的面积》选择专项练习题(附答案)
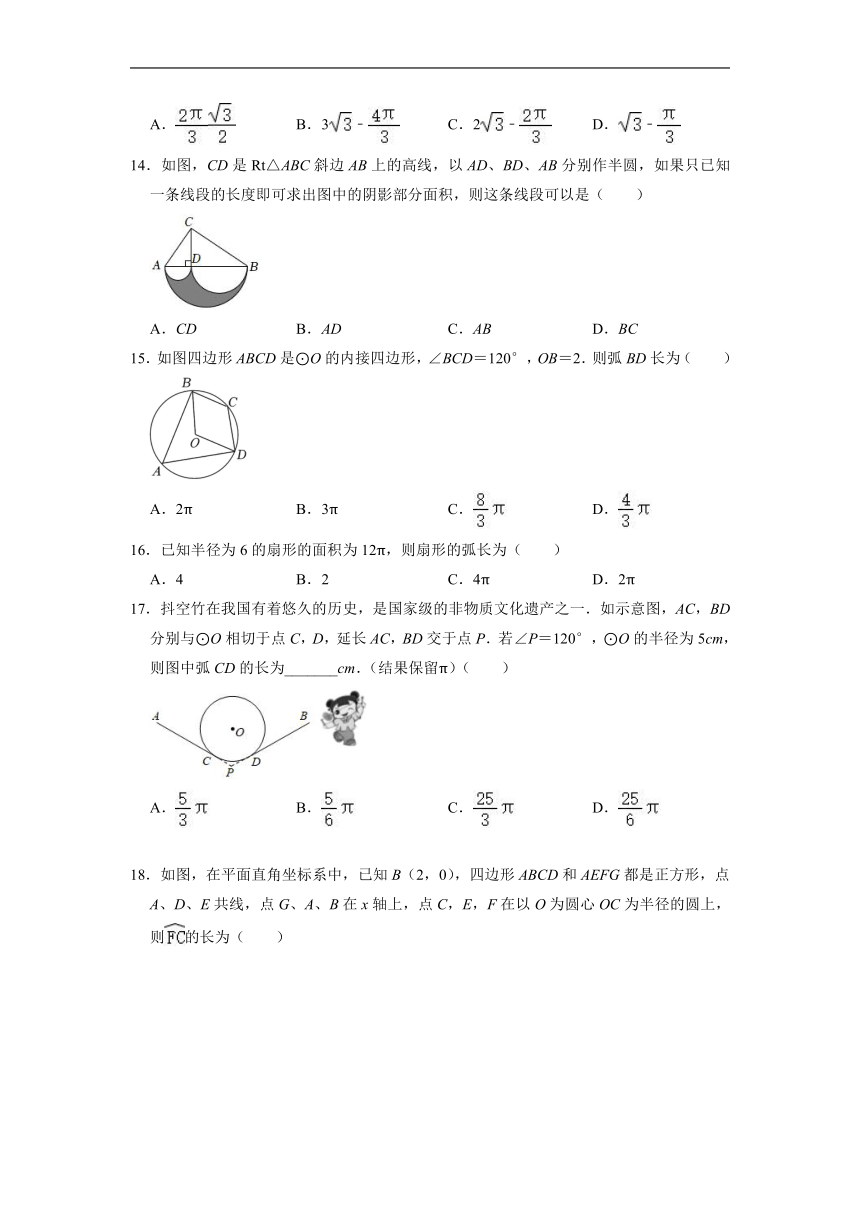
1.如图,一条公路(公路的宽度忽略不计)的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,半径OA=90m,圆心角∠AOB=80°,则这段弯路()的长度为( )
A.20πm B.30πm C.40πm D.50πm
2.如图,四边形ABCD中,∠A=60°,AB∥CD,DE⊥AD交AB于点E,以点E为圆心,DE为半径,且DE=6的圆交CD于点F,则阴影部分的面积为( )
A.6π﹣9 B.12π﹣9 C.6π﹣ D.12π﹣
3.如图,在平行四边形ABCD中,AD=6,以AD为直径的⊙O恰好经过点B,交BC于点E,当点E为的中点时,下列结论错误的是( )
A.AE平分∠BAD B.
C. D.的长为2π
4.如图所示的曲边三角形可按下述方法作出:作等边△ABC,分别以点A,B,C为圆心,以AB长为半径作,,,三弧所围成的图形就是一个曲边三角形.如果一个曲边三角形的周长为2π,则此曲边三角形的面积为( )
A.2π﹣2 B.2π﹣ C.2π D.π﹣
5.家具厂利用如图所示直径为1米的圆形材料加工成一种扇形家具部件,已知扇形的圆心角∠BAC=90°,则扇形部件的面积为( )
A.米2 B.米2 C.米2 D.米2
6.如图,在扇形AOB中,∠AOB=90°,OA=6,点D在OA上,点C在弧AB上,且点C,O关于直线BD对称,连接CD,则图中阴影部分的面积是( )
A.6π﹣3 B.6π﹣6 C.3π﹣6 D.3π﹣3
7.某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图.已知矩形的宽为2m,高为2m,则改建后门洞的圆弧长是( )
A.m B.m C.m D.(+2)m
8.已知扇形的半径为6,圆心角为120°,则它的弧长是( )
A.2π B.4π C.6π D.8π
9.如果一个扇形的圆心角为30°,面积是,那么这个扇形的弧长是( )
A. B. C. D.
10.山西著名工艺品平遥推光漆器外观古朴雅致、闪光发亮,绘饰金碧辉煌,以手掌推出光泽而得名.图1是平遥推光漆器的一种图案,图2是选取其某部分并且放大后的示意图.四边形ABCD是边长为2的正方形,分别以正方形的四个顶点为圆心,对角线的长为半径画弧,四条弧相交于点O,则图中阴影部分的面积为( )
A.2π﹣4 B.π﹣2 C.2π D.
11.如图,⊙O的半径为6,PA,PB分别切⊙O于点A,B.若∠P=50°,则的长为( )
A. B. C.5π D.
12.如图,在边长为1的正方形ABCD中,对角线AC的中点为O,分别以点A,C为圆心,以AO的长为半径画弧,分别与正方形的边相交,则图中的阴影部分的面积为( )
A.1﹣ B.1﹣ C.4﹣π D.2﹣
如图,在菱形ABCD中,∠A=60°,AB=2.以点A为圆心,AB为半径作,向菱形内部作,使=,则图中阴影部分的面积为( )
A. B.3﹣ C.2﹣ D.﹣
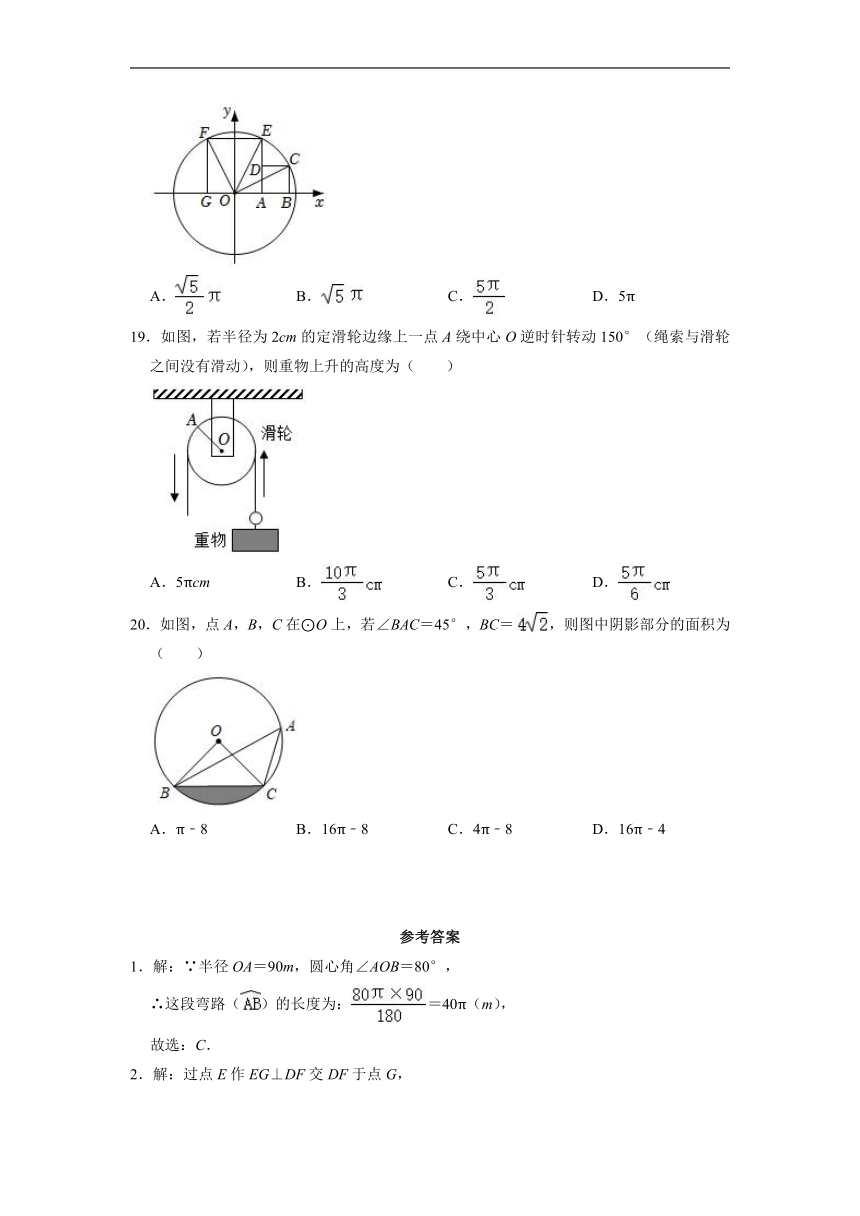
14.如图,CD是Rt△ABC斜边AB上的高线,以AD、BD、AB分别作半圆,如果只已知一条线段的长度即可求出图中的阴影部分面积,则这条线段可以是( )
A.CD B.AD C.AB D.BC
15.如图四边形ABCD是⊙O的内接四边形,∠BCD=120°,OB=2.则弧BD长为( )
A.2π B.3π C. D.
16.已知半径为6的扇形的面积为12π,则扇形的弧长为( )
A.4 B.2 C.4π D.2π
17.抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如示意图,AC,BD分别与⊙O相切于点C,D,延长AC,BD交于点P.若∠P=120°,⊙O的半径为5cm,则图中弧CD的长为_______cm.(结果保留π)( )
A. B. C. D.
18.如图,在平面直角坐标系中,已知B(2,0),四边形ABCD和AEFG都是正方形,点A、D、E共线,点G、A、B在x轴上,点C,E,F在以O为圆心OC为半径的圆上,则的长为( )
A. B. C. D.5π
19.如图,若半径为2cm的定滑轮边缘上一点A绕中心O逆时针转动150°(绳索与滑轮之间没有滑动),则重物上升的高度为( )
A.5πcm B. C. D.
20.如图,点A,B,C在⊙O上,若∠BAC=45°,BC=,则图中阴影部分的面积为( )
A.π﹣8 B.16π﹣8 C.4π﹣8 D.16π﹣4
参考答案
1.解:∵半径OA=90m,圆心角∠AOB=80°,
∴这段弯路()的长度为:=40π(m),
故选:C.
2.解:过点E作EG⊥DF交DF于点G,
∵∠A=60°,AB∥CD,DE⊥AD交AB于点E,
∴∠GDE=∠DEA=30°,
∵DE=EF,
∴∠EDF=∠EFD=30°,
∴∠DEF=120°,
∵∠GDE=30°,DE=6,
∴GE=3,DG=3,
∴DF=6,
阴影部分的面积=﹣×6×3=12π﹣9,
故选:B.
3.解:A.∵点E为的中点,
∴,
∴∠BAE=∠EAD,
∴AE平分∠BAD,
故A不符合题意;
B.∵四边形ABCD是平行四边形,
∴BE∥AO,
∴∠BEA=∠EAO,
∵∠BAE=∠EAO,
∴∠BAE=∠BEA,
∴,
∴△AOB和△BOE是等边三角形,
∴OA=BE,
∵BC=AD,
∴EC=OD,
∵EC∥OD,
∴四边形ECDO是平行四边形,
∵△AOB和△BOE是等边三角形,
∴∠EOD=60°,
∵OE=3,
∴EH=,
∴S阴影=OD×EH﹣=
故B符合题意;
C.由B可知,,
故C不符合题意;
D.的长为:=2π,
故D不符合题意.
故选:B.
4.解:设等边三角形ABC的边长为r,
∴=,解得r=2,即正三角形的边长为2,
∴这个曲边三角形的面积=2××+(﹣)×3=2π﹣2,
故选:A.
5.解:连结BC,AO,如图所示,
∵∠BAC=90°,
∴BC是⊙O的直径,
∵⊙O的直径为1米,
∴AO=BO=(米),
∴AB==(米),
∴扇形部件的面积=π×()2=(米2),
故选:C.
6.解:连接BD,OC,交BD于点E,
∵点C,O关于直线BD对称,
∴BD垂直平分OC,即OE=CE,OC⊥BD,
∵OE=CE=OC=OB,
∴∠OBE=30°,
∴∠BOC=90°﹣30°=60°,
∵OB=OA=6,
在Rt△BOD中,OB=6,∠OBD=90°﹣60°=30°,
∴OD=2,
在Rt△DOE中,OD=2,∠DOE=90°﹣60°=30°,
∴DE=OD=,
∴S阴影部分=S扇形AOC﹣S△OCD
=﹣×6×
=3π﹣3.
故选:D.
7.解:连接AC,BD,AC和BD相交于点O,则O为圆心,如图所示,
由题意可得,CD=2m,AD=2m,∠ADC=90°,
∴tan∠DCA===,AC==4(m),
∴∠ACD=60°,OA=OC=2m,
∴∠ACB=30°,
∴∠AOB=60°,
∴优弧ADCB所对的圆心角为300°,
∴改建后门洞的圆弧长是:=(m),
故选:C.
8.解:由弧长公式可知,
l==4π,
故选:B.
9.解:∵一个扇形的圆心角为30°,面积是,
∴πR2=,
∴R=2,
∴扇形的弧长=×π×2=(m),
故选:A.
10.解:正方形的对角线长为,
扇形的半径为=,
故两块空白部分的面积为=4﹣π,
所以四块空白部分的面积为2(4﹣π)=8﹣2π,
所以阴影部分的面积为为22﹣(8﹣2π)=2π﹣4.
故选:A.
11.解:如图,连接OA、OB,
∵PA、PB是圆O的切线,
∴∠PBO=∠PAO=90°,
∵∠P=50°,
∴∠AOB=130°,
∴的长为:=.
故选:A.
12.解:∵四边形ABCD为正方形,
∴AB=BC=1,∠DAB=∠DCB=90°,
由勾股定理得,AC=,
∴OA=OC=,
∴图中的阴影部分的面积=12﹣×2=,
故选:A.
13.解:如图所示:连接BD,
∵四边形ABCD是菱形,
∴AB=AD,
∵∠BAD=60°,
∴△ABD是等边三角形,
∴AB=BD=2,
∴S阴影=S菱形﹣S扇形BAD﹣S弓形BEC=2××2﹣﹣(﹣)=.
故选:B.
14.解:S阴影部分=S大半圆﹣S小半圆1﹣S小半圆2
=π×()2﹣π×()2﹣π×()2
=π×(AB2﹣AD2﹣BD2)
=π×[(AD+BD)2﹣AD2﹣BD2]
=π×(2AD BD)
=π(AD BD),
∵CD是Rt△ABC斜边AB上的高线,
∴CD2=AD BD,
∴只要已知CD的长即可,
故选:A.
15.解:∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠BCD=180°,
∴∠A=180°﹣∠BCD=180°﹣120°=60°,
由圆周角定理得,∠BOD=2∠A=120°,
∴弧BD的长为=π,
故选:D.
16.解:设扇形的弧长为l,由扇形面积公式可得,
=12π,
解得l=4π,
故选:C.
17.解:连接OC,OD,
∵AC、BD分别与⊙O相切于点C、D,
∴∠OCP=∠ODP=90°,
由四边形内角和为360°可得,
∠COD=360°﹣∠OCP﹣∠ODP﹣∠CPD=360°﹣90°﹣90°﹣120°=60°,
∴==π,
故选:A.
18.解:设点A(a,0),则AB=2﹣a,
根据题意可得,
BC=AB=2﹣a,
在Rt△OBC中,
OC2=OB2+BC2=22+(2﹣a)2=8﹣4a+a2,
∵OE=OC,
在Rt△OAE中,AE=AG=2a,
∴OE2=OA2+AE2,
∴8﹣4a+a2=a2+(2a)2,
解得:a=1,a=﹣2(舍去),
∴点A(1,0),AB=1,
∴OC==,
在△OBC和△EGO中,
,
△OBC≌△EGO(SAS),
∴∠EOG=∠OCB,
∵∠COB+∠OCB=90°,
∴∠COB+∠FOG=90°,
∴∠FOC=90°,
∴弧FC的长===.
故选:A.
19.解:根据题意得:l==(cm),
则重物上升了cm,
故选:C.
20.解:∵∠BAC=45°,
∴∠BOC=2∠BAC=90°,
∵OB=OC,OB2+OC2=BC2,BC=,
∴2OB2=(4)2,
解得OB=4,
∴S阴影=S扇形BOC﹣S△BOC
=﹣
=4π﹣8.
故选:C.
1.如图,一条公路(公路的宽度忽略不计)的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,半径OA=90m,圆心角∠AOB=80°,则这段弯路()的长度为( )
A.20πm B.30πm C.40πm D.50πm
2.如图,四边形ABCD中,∠A=60°,AB∥CD,DE⊥AD交AB于点E,以点E为圆心,DE为半径,且DE=6的圆交CD于点F,则阴影部分的面积为( )
A.6π﹣9 B.12π﹣9 C.6π﹣ D.12π﹣
3.如图,在平行四边形ABCD中,AD=6,以AD为直径的⊙O恰好经过点B,交BC于点E,当点E为的中点时,下列结论错误的是( )
A.AE平分∠BAD B.
C. D.的长为2π
4.如图所示的曲边三角形可按下述方法作出:作等边△ABC,分别以点A,B,C为圆心,以AB长为半径作,,,三弧所围成的图形就是一个曲边三角形.如果一个曲边三角形的周长为2π,则此曲边三角形的面积为( )
A.2π﹣2 B.2π﹣ C.2π D.π﹣
5.家具厂利用如图所示直径为1米的圆形材料加工成一种扇形家具部件,已知扇形的圆心角∠BAC=90°,则扇形部件的面积为( )
A.米2 B.米2 C.米2 D.米2
6.如图,在扇形AOB中,∠AOB=90°,OA=6,点D在OA上,点C在弧AB上,且点C,O关于直线BD对称,连接CD,则图中阴影部分的面积是( )
A.6π﹣3 B.6π﹣6 C.3π﹣6 D.3π﹣3
7.某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图.已知矩形的宽为2m,高为2m,则改建后门洞的圆弧长是( )
A.m B.m C.m D.(+2)m
8.已知扇形的半径为6,圆心角为120°,则它的弧长是( )
A.2π B.4π C.6π D.8π
9.如果一个扇形的圆心角为30°,面积是,那么这个扇形的弧长是( )
A. B. C. D.
10.山西著名工艺品平遥推光漆器外观古朴雅致、闪光发亮,绘饰金碧辉煌,以手掌推出光泽而得名.图1是平遥推光漆器的一种图案,图2是选取其某部分并且放大后的示意图.四边形ABCD是边长为2的正方形,分别以正方形的四个顶点为圆心,对角线的长为半径画弧,四条弧相交于点O,则图中阴影部分的面积为( )
A.2π﹣4 B.π﹣2 C.2π D.
11.如图,⊙O的半径为6,PA,PB分别切⊙O于点A,B.若∠P=50°,则的长为( )
A. B. C.5π D.
12.如图,在边长为1的正方形ABCD中,对角线AC的中点为O,分别以点A,C为圆心,以AO的长为半径画弧,分别与正方形的边相交,则图中的阴影部分的面积为( )
A.1﹣ B.1﹣ C.4﹣π D.2﹣
如图,在菱形ABCD中,∠A=60°,AB=2.以点A为圆心,AB为半径作,向菱形内部作,使=,则图中阴影部分的面积为( )
A. B.3﹣ C.2﹣ D.﹣
14.如图,CD是Rt△ABC斜边AB上的高线,以AD、BD、AB分别作半圆,如果只已知一条线段的长度即可求出图中的阴影部分面积,则这条线段可以是( )
A.CD B.AD C.AB D.BC
15.如图四边形ABCD是⊙O的内接四边形,∠BCD=120°,OB=2.则弧BD长为( )
A.2π B.3π C. D.
16.已知半径为6的扇形的面积为12π,则扇形的弧长为( )
A.4 B.2 C.4π D.2π
17.抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如示意图,AC,BD分别与⊙O相切于点C,D,延长AC,BD交于点P.若∠P=120°,⊙O的半径为5cm,则图中弧CD的长为_______cm.(结果保留π)( )
A. B. C. D.
18.如图,在平面直角坐标系中,已知B(2,0),四边形ABCD和AEFG都是正方形,点A、D、E共线,点G、A、B在x轴上,点C,E,F在以O为圆心OC为半径的圆上,则的长为( )
A. B. C. D.5π
19.如图,若半径为2cm的定滑轮边缘上一点A绕中心O逆时针转动150°(绳索与滑轮之间没有滑动),则重物上升的高度为( )
A.5πcm B. C. D.
20.如图,点A,B,C在⊙O上,若∠BAC=45°,BC=,则图中阴影部分的面积为( )
A.π﹣8 B.16π﹣8 C.4π﹣8 D.16π﹣4
参考答案
1.解:∵半径OA=90m,圆心角∠AOB=80°,
∴这段弯路()的长度为:=40π(m),
故选:C.
2.解:过点E作EG⊥DF交DF于点G,
∵∠A=60°,AB∥CD,DE⊥AD交AB于点E,
∴∠GDE=∠DEA=30°,
∵DE=EF,
∴∠EDF=∠EFD=30°,
∴∠DEF=120°,
∵∠GDE=30°,DE=6,
∴GE=3,DG=3,
∴DF=6,
阴影部分的面积=﹣×6×3=12π﹣9,
故选:B.
3.解:A.∵点E为的中点,
∴,
∴∠BAE=∠EAD,
∴AE平分∠BAD,
故A不符合题意;
B.∵四边形ABCD是平行四边形,
∴BE∥AO,
∴∠BEA=∠EAO,
∵∠BAE=∠EAO,
∴∠BAE=∠BEA,
∴,
∴△AOB和△BOE是等边三角形,
∴OA=BE,
∵BC=AD,
∴EC=OD,
∵EC∥OD,
∴四边形ECDO是平行四边形,
∵△AOB和△BOE是等边三角形,
∴∠EOD=60°,
∵OE=3,
∴EH=,
∴S阴影=OD×EH﹣=
故B符合题意;
C.由B可知,,
故C不符合题意;
D.的长为:=2π,
故D不符合题意.
故选:B.
4.解:设等边三角形ABC的边长为r,
∴=,解得r=2,即正三角形的边长为2,
∴这个曲边三角形的面积=2××+(﹣)×3=2π﹣2,
故选:A.
5.解:连结BC,AO,如图所示,
∵∠BAC=90°,
∴BC是⊙O的直径,
∵⊙O的直径为1米,
∴AO=BO=(米),
∴AB==(米),
∴扇形部件的面积=π×()2=(米2),
故选:C.
6.解:连接BD,OC,交BD于点E,
∵点C,O关于直线BD对称,
∴BD垂直平分OC,即OE=CE,OC⊥BD,
∵OE=CE=OC=OB,
∴∠OBE=30°,
∴∠BOC=90°﹣30°=60°,
∵OB=OA=6,
在Rt△BOD中,OB=6,∠OBD=90°﹣60°=30°,
∴OD=2,
在Rt△DOE中,OD=2,∠DOE=90°﹣60°=30°,
∴DE=OD=,
∴S阴影部分=S扇形AOC﹣S△OCD
=﹣×6×
=3π﹣3.
故选:D.
7.解:连接AC,BD,AC和BD相交于点O,则O为圆心,如图所示,
由题意可得,CD=2m,AD=2m,∠ADC=90°,
∴tan∠DCA===,AC==4(m),
∴∠ACD=60°,OA=OC=2m,
∴∠ACB=30°,
∴∠AOB=60°,
∴优弧ADCB所对的圆心角为300°,
∴改建后门洞的圆弧长是:=(m),
故选:C.
8.解:由弧长公式可知,
l==4π,
故选:B.
9.解:∵一个扇形的圆心角为30°,面积是,
∴πR2=,
∴R=2,
∴扇形的弧长=×π×2=(m),
故选:A.
10.解:正方形的对角线长为,
扇形的半径为=,
故两块空白部分的面积为=4﹣π,
所以四块空白部分的面积为2(4﹣π)=8﹣2π,
所以阴影部分的面积为为22﹣(8﹣2π)=2π﹣4.
故选:A.
11.解:如图,连接OA、OB,
∵PA、PB是圆O的切线,
∴∠PBO=∠PAO=90°,
∵∠P=50°,
∴∠AOB=130°,
∴的长为:=.
故选:A.
12.解:∵四边形ABCD为正方形,
∴AB=BC=1,∠DAB=∠DCB=90°,
由勾股定理得,AC=,
∴OA=OC=,
∴图中的阴影部分的面积=12﹣×2=,
故选:A.
13.解:如图所示:连接BD,
∵四边形ABCD是菱形,
∴AB=AD,
∵∠BAD=60°,
∴△ABD是等边三角形,
∴AB=BD=2,
∴S阴影=S菱形﹣S扇形BAD﹣S弓形BEC=2××2﹣﹣(﹣)=.
故选:B.
14.解:S阴影部分=S大半圆﹣S小半圆1﹣S小半圆2
=π×()2﹣π×()2﹣π×()2
=π×(AB2﹣AD2﹣BD2)
=π×[(AD+BD)2﹣AD2﹣BD2]
=π×(2AD BD)
=π(AD BD),
∵CD是Rt△ABC斜边AB上的高线,
∴CD2=AD BD,
∴只要已知CD的长即可,
故选:A.
15.解:∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠BCD=180°,
∴∠A=180°﹣∠BCD=180°﹣120°=60°,
由圆周角定理得,∠BOD=2∠A=120°,
∴弧BD的长为=π,
故选:D.
16.解:设扇形的弧长为l,由扇形面积公式可得,
=12π,
解得l=4π,
故选:C.
17.解:连接OC,OD,
∵AC、BD分别与⊙O相切于点C、D,
∴∠OCP=∠ODP=90°,
由四边形内角和为360°可得,
∠COD=360°﹣∠OCP﹣∠ODP﹣∠CPD=360°﹣90°﹣90°﹣120°=60°,
∴==π,
故选:A.
18.解:设点A(a,0),则AB=2﹣a,
根据题意可得,
BC=AB=2﹣a,
在Rt△OBC中,
OC2=OB2+BC2=22+(2﹣a)2=8﹣4a+a2,
∵OE=OC,
在Rt△OAE中,AE=AG=2a,
∴OE2=OA2+AE2,
∴8﹣4a+a2=a2+(2a)2,
解得:a=1,a=﹣2(舍去),
∴点A(1,0),AB=1,
∴OC==,
在△OBC和△EGO中,
,
△OBC≌△EGO(SAS),
∴∠EOG=∠OCB,
∵∠COB+∠OCB=90°,
∴∠COB+∠FOG=90°,
∴∠FOC=90°,
∴弧FC的长===.
故选:A.
19.解:根据题意得:l==(cm),
则重物上升了cm,
故选:C.
20.解:∵∠BAC=45°,
∴∠BOC=2∠BAC=90°,
∵OB=OC,OB2+OC2=BC2,BC=,
∴2OB2=(4)2,
解得OB=4,
∴S阴影=S扇形BOC﹣S△BOC
=﹣
=4π﹣8.
故选:C.
同课章节目录
