第1章 二次函数 单元检测卷(含解析)
文档属性
| 名称 | 第1章 二次函数 单元检测卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 407.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 22:20:06 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版2022年九年级上册第1章《二次函数》单元检测卷
满分120分
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)若y=(m﹣1)是二次函数,则m的值是( )
A.1 B.﹣1 C.1或﹣1 D.2
2.(3分)抛物线y=﹣x2+5x﹣3与y轴的交点坐标是( )
A.(0,3) B.(0,﹣3) C.(0,﹣5) D.(0,5)
3.(3分)抛物线y=﹣5(x﹣1)2+2的顶点坐标为( )
A.(﹣1,2) B.(1,﹣2) C.(1,2) D.(2,1)
4.(3分)将二次函数的图象向右平移1个单位,所得图象的解析式为( )
A. B.
C. D.
5.(3分)已知抛物线y=ax2+bx+c过点A(2,3),B(4,3),则该抛物线的对称轴为( )
A.直线x=1 B.直线x=2 C.直线x=3 D.直线x=4
6.(3分)在同一直角坐标系中,一次函数y=ax﹣b和二次函数y=ax2﹣b的图象大致为( )
A.B. C.D.
7.(3分)若抛物线y=ax2﹣x+1与x轴有公共点,则a的取值范围是( )
A.a<且a≠0 B.a≤ C.a≤且a≠0 D.a≥
8.(3分)已知二次函数y=x2﹣4x﹣1,当1<x≤5时,对应的函数值y不可能是( )
A.﹣5 B.﹣4 C.4 D.5
9.(3分)太原某中学利用学校的体育场地设施和设备,充分调动全体师生的积极性,广泛开展各项体育活动,努力提高学生的身体素质,如图①是小杰在铅球比赛中的一次掷球,铅球出手以后的轨迹可近似看作是抛物线的一部分,已知铅球出手时离地面1.6米,铅球离抛掷点水平距离3米时达到最高,此时铅球离地面2.5米,如图②,以水平面为x轴,小杰所站位置的铅垂线为y轴建立平面直角坐标系,则他掷铅球的运动路线的函数表达式为( )
A. B.
C. D.
10.(3分)如图是二次函数y=ax2+bx+c的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a﹣2b+c<0;④若(﹣3,y1),(4,y2)是抛物线上两点,则y1<y2,其中结论正确的是( )
A.①② B.②③④ C.②④ D.①③④
二.填空题(共5小题,满分15分,每小题3分)
11.(3分)在二次函数y=(x﹣1)2+5中,当x>2时,y随x的增大而 (填“增大”或“减小”).
12.(3分)将二次函数化成y=a(x﹣h)2+k的形式,y= .
13.(3分)把y=(3x﹣2)(x+3)化成一般形式后,一次项系数与常数项的和为 .
14.(3分)已知二次函数y=3(x+1)2的图象上有三点A(1,y1),B(2,y2),C(﹣2,y3),则y1,y2,y3的大小关系为 .
15.(3分)设max{x,y}表示x,y两个数中的最大值.例如“max{1,3}=3,max{﹣2,0,}=”.则关于x的函数y=max{2x,﹣x﹣2,﹣x2}的最小值为 .
三.解答题(共8小题,满分75分)
16.(8分)已知抛物线y=﹣x2+2x+2.
(1)写出它的开口方向、对称轴和顶点坐标;
(2)当x为何值时,函数y=﹣x2+2x+2取得最大值,请求出这个最大值.
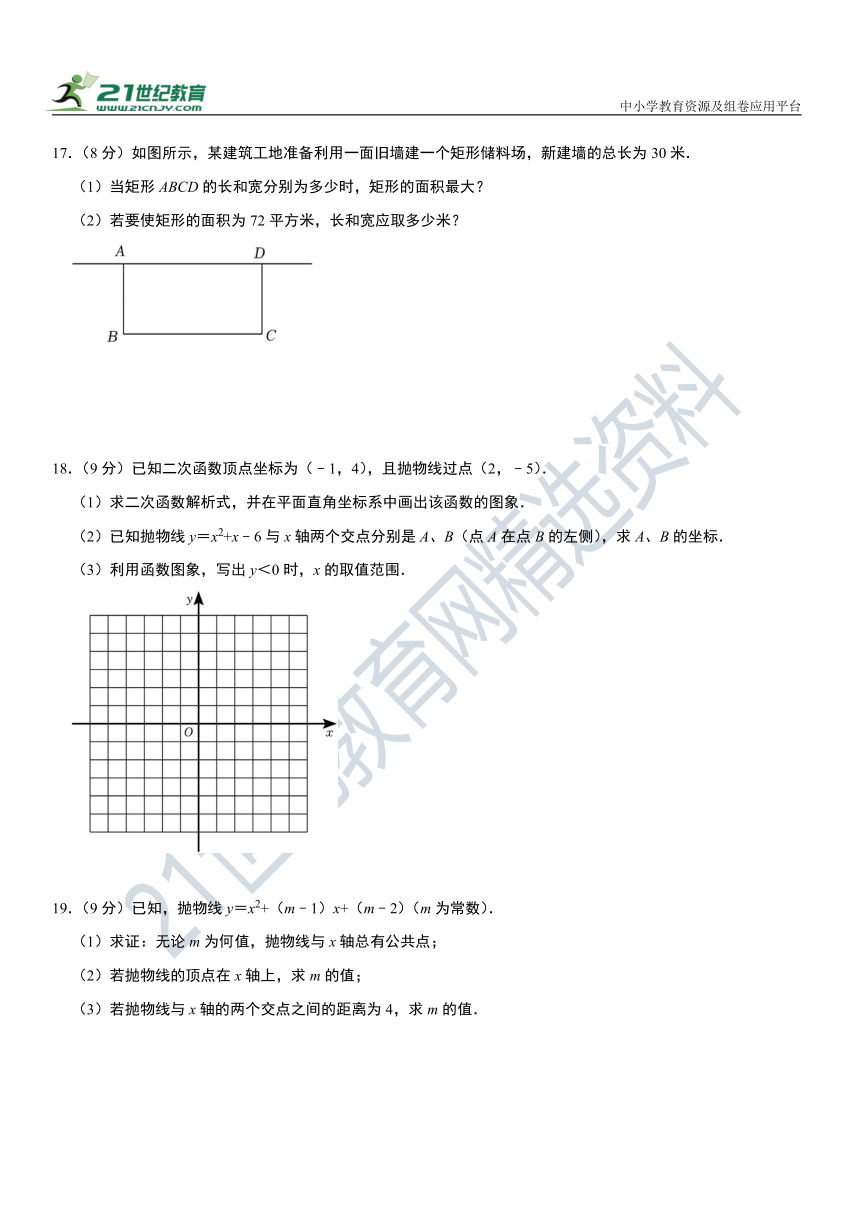
17.(8分)如图所示,某建筑工地准备利用一面旧墙建一个矩形储料场,新建墙的总长为30米.
(1)当矩形ABCD的长和宽分别为多少时,矩形的面积最大?
(2)若要使矩形的面积为72平方米,长和宽应取多少米?
18.(9分)已知二次函数顶点坐标为(﹣1,4),且抛物线过点(2,﹣5).
(1)求二次函数解析式,并在平面直角坐标系中画出该函数的图象.
(2)已知抛物线y=x2+x﹣6与x轴两个交点分别是A、B(点A在点B的左侧),求A、B的坐标.
(3)利用函数图象,写出y<0时,x的取值范围.
19.(9分)已知,抛物线y=x2+(m﹣1)x+(m﹣2)(m为常数).
(1)求证:无论m为何值,抛物线与x轴总有公共点;
(2)若抛物线的顶点在x轴上,求m的值;
(3)若抛物线与x轴的两个交点之间的距离为4,求m的值.
20.(9分)已知二次函数y=x2﹣2x﹣3的图象与x轴交于A、B两点,与y轴交于点C,求:
(1)点A、B、C的坐标;
(2)△ABC的面积.
21.(10分)某超市经销一种销售成本为每件40元的商品.据市场调查分析,如果按每件50元销售,一周能售出500件;若销售单价每涨1元,每周销售量就减少10件.
(1)当销售单价为52元时,销售量为 件,总利润为 元;
(2)要使得一周的销售利润达到8000元,销售单价应定为多少元?
(3)该超市为了获得最大利润,应将销售单价定为多少元?
22.(10分)如图,在平面直角坐标系中,已知抛物线与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.
(1)求该抛物线的函数表达式;
(2)点P是直线BC下方抛物线上的任意一点,连结PB,PC,以PB,PC为邻边作平行四边形CPBD,求四边形CPBD面积的最大值;
23.(12分)我们将使得函数值为零的自变量的值称为函数的零点.例如,对于函数y=x﹣1,令y=0,可得x=1,我们就说1是函数y=x﹣1的零点.
(1)求一次函数y=2x﹣3的零点;
(2)若二次函数y=x2+bx+b的零点为x1,x2,A,B两点的坐标依次A(x1,0),B(x2,0),如果AB=2,求b的值;
(3)直线y=﹣2x+b的零点为1,且与抛物线y=kx2﹣(3k+3)x+2k+4(k≠0)交于C、D两点,若m+1≤≤m+2时,线段CD有最小值3,求m.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:∵y=(m﹣1)是二次函数,
∴m2+1=2且m﹣1≠0,
解得m=﹣1或m=1(舍),
∴m=﹣1,
故选:B.
2.【解答】解:在y=﹣x2+5x﹣3中,令x=0,得y=﹣3,
∴该抛物线与y轴的交点坐标为(0,﹣3).
故选:B.
3.【解答】解:∵y=﹣5(x﹣1)2+2,
∴此函数的顶点坐标是(1,2).
故选:C.
4.【解答】解:将二次函数的图象向右平移1个单位,所得图象的解析式为:.
故选:A.
5.【解答】解:∵抛物线y=ax2+bx+c过点A(2,3),B(4,3),
∴此两点关于抛物线的对称轴对称,
∴对称轴为直线x==3.
故选:C.
6.【解答】解:A、由一次函数y=ax﹣b的图象可得:a>0,﹣b>0,此时二次函数y=ax2﹣b的图象应该开口向上,故A错误;
B、由一次函数y=ax﹣b的图象可得:a<0,﹣b>0,此时二次函数y=ax2﹣b的图象应该开口向下,故B错误;
C、由一次函数y=ax﹣b的图象可得:a<0,﹣b>0,此时二次函数y=ax2﹣b的图象应该开口向下,故C错误;
D、由一次函数y=ax﹣b的图象可得:a<0,﹣b>0,此时二次函数y=ax2﹣b的图象应该开口向下,顶点的纵坐标﹣b大于零,故D正确;
故选:D.
7.【解答】解:根据题意,得Δ=(﹣1)2﹣4a≥0且a≠0.
解得a≤且a≠0.
故选:C.
8.【解答】解:∵y=x2﹣4x﹣1=(x﹣2)2﹣5,
∴抛物线开口向上,顶点坐标为(2,﹣5),
将x=5代入y=x2﹣4x﹣1得y=4,
∴当1<x≤5时,﹣5≤y≤4,
故选:D.
9.【解答】解:根据题意,得B(0,1.6),C(3,2.5)
设抛物线解析式为y=a(x﹣3)2+2.5,
将B点代入解析式得:9a+2.5=1.6,
解得a=﹣,
∴小杰掷铅球的运动路线的解析式为y=﹣(x﹣3)2+2.5=﹣x2+x+.
故选:A.
10.【解答】解:①∵抛物线开口向下,对称轴为直线x=1,与y轴交于正半轴,
∴a<0,﹣=1,c>0,
∴b=﹣2a>0,
∴abc<0,结论①错误;
②抛物线对称轴为直线x=1,
∴﹣=1,
∴b=﹣2a,
∴2a+b=0,结论②正确;
③∵当x=﹣2时,y<0,
∴4a﹣2b+c<0,结论③正确;
④∵抛物线的对称轴为直线x=1,抛物线开口向下,且1﹣(﹣3)>4﹣1,
∴y1<y2,结论④正确;
综上所述:正确的结论有②③④,
故选:B.
二.填空题(共5小题,满分15分,每小题3分)
11.【解答】解:根据二次函数解析式为y=(x﹣1)2+5,
可知,顶点坐标(1,5),对称轴是直线x=1,
又a=1>0,抛物线开口向上,
所以,当x>2时,y随x的增大而增大.
故答案为:增大.
12.【解答】解:=(x2﹣12x+36﹣36)+21=(x﹣6)2+3,
所以y=(x﹣6)2+3.
故答案为:(x﹣6)2+3.
13.【解答】解:y=(3x﹣2)(x+3)
=3x2+7x﹣6,
其中一次项系数为7,常数项为﹣6,
∴一次项系数与常数项的和为:7+(﹣6)=1,
故答案为:1.
14.【解答】解:由二次函数y=3(x+1)2可知,对称轴为x=﹣1,开口向上,
∵二次函数y=3(x+1)2的图象上有三点A(1,y1),B(2,y2),C(﹣2,y3),
∴C(﹣2,y3)关于对称轴的对称点为(0,y3),
∵﹣1<0<1<2,
∴y3<y1<y2.
故答案为:y3<y1<y2.
15.【解答】解:将y=2x,y=﹣x﹣2和y=﹣x2画在同一个坐标系中,如图所示,
易得点A的坐标为(﹣1,﹣1),点B的坐标为(0,0),
由题意可知,
关于x的函数y=max{2x,﹣x﹣2,﹣x2},即y=2x,y=﹣x﹣2和y=﹣x2的不同范围内的部分图形,
即当x≤﹣1时,y=﹣x﹣2,当x=﹣1时,有最小值,为﹣1;
当﹣1≤x≤0时,y=﹣x2,当x=﹣1时,有最小值,为﹣1;
当x>0时,y=2x,当x=0时,有最小值,为0.
综上关于x的函数y=max{2x,﹣x﹣2,﹣x2}的最小值为﹣1.
三.解答题(共8小题,满分75分)
16.【解答】解:(1)y=﹣x2+2x+2=﹣(x﹣1)2+3,
所以抛物线的开口向下,对称轴为直线x=1,顶点坐标为(1,3);
(2)由(1)可知,当x=1时,函数y=﹣x2+2x+2取得最大值,最大值是3.
17.【解答】解:(1)设AB=x米,则BC=(30﹣2x)米,矩形ABCD的面积为S平方米,
根据题意得:S=x(30﹣2x)=﹣2x2+30x=﹣2(x﹣)2+,
∵﹣2<0,
∴当x=时,S最大,最大值为,
此时30﹣2x=15,
∴矩形ABCD的长为15米,宽为米时,矩形的面积最大;
(2)设AB=x米,则BC=(30﹣2x)米,
根据题意得:x(30﹣2x)=72,
解得:x1=3,x2=12,
当x=3时,30﹣2x=24,
当x=12时,30﹣2x=6,
∵BC>AB,
∴x=3,
答:矩形的长为24米,宽为3米时矩形的面积为72平方米.
18.【解答】解:(1)∵二次函数的图象的顶点坐标为(﹣1,4).
∴设二次函数的解析式为y=a(x+1)2+4,
把(2,﹣5)代入得,﹣5=a(2+1)2+4,
解得a=﹣1,
∴这个函数的解析式为y=﹣(x+1)2+4=﹣x2﹣2x+3,
函数的图象如图:
.
(2)y=x2+x﹣6,令y=0,则x=2或﹣3,
即A(﹣3,0),B(2,0);
(3)由图象可以看出:y<0时,x的取值范围为:x>1或x<﹣3.
19.【解答】(1)证明:令x2+(m﹣1)x+(m﹣2)=0,
则Δ=(m﹣1)2﹣4(m﹣2)=m2﹣2m+1﹣4m+8=m2﹣6m+9=(m﹣3)2,
∵Δ=(m﹣3)2≥0,
∴无论m为何值,抛物线与x轴总有公共点.
(2)解:当抛物线顶点在x轴上时,抛物线与x轴只有1个公共点,
∴(m﹣3)2=0,
∴m=3.
(3)解:∵y=x2+(m﹣1)x+(m﹣2)=(x+m﹣2)(x+1),
∴抛物线与x轴交点坐标为(2﹣m,0),(﹣1,0),
若抛物线与x轴的两个交点之间的距离为4,则2﹣m﹣(﹣1)=4或﹣1﹣(2﹣m)=4,
解得m=﹣1或m=7.
20.【解答】解:(1)令x=0,则y=﹣3,
∴C(0,﹣3);
令y=0,则x2﹣2x﹣3=0,
解得:x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0);
(2)∵A(﹣1,0),B(3,0),C(0,﹣3),
∴AB=4,OC=3,
∴S△ABC=AB OC=×4×3=6.
21.【解答】解:(1)由题意得:当售价为52元时,销售量为500﹣(52﹣50)×10=480(件),
销售利润为(50﹣40)×480=4800(元).
故答案为:480,4800;
(2)设销售单价为x元,一周的销售量为y件,
根据题意题意得:y=500﹣10(x﹣50)=﹣10x+1000,(50≤x≤100),
则(x﹣40)(﹣10x+1000)=8000,
解得x1=60,x2=80,
答:销售单价应定为60元或80元;
(3)设一周利润为w元,
根据题意得:w=(x﹣40)(﹣10x+1000)=﹣10x2+1400x﹣40000=﹣10(x﹣70)2+9000,
∵﹣10<0,
∴当x=70时,w有最大值,最大值为9000,
答:该超市为了获得最大利润,应将销售单价定为70元.
22.【解答】解:(1)将A(﹣1,0),B(3,0)代入,
∴,
解得,
∴y=x2﹣x﹣2;
(2)过P作PE∥y轴交直线BC于点E,
令x=0,则y=﹣2,
∴C(0,﹣2),
设直线BC的解析式为y=kx+b,
,
解得,
∴y=x﹣2,
设P(t,t2﹣t﹣2),则E(t,t﹣2),
∴PE=﹣t2+2t,
∴S△PBC=3(﹣t2+2t)=﹣t2+3t,
∵S平行四边形CPBD=2S△PBC=﹣2t2+6t=﹣2(t﹣)2+,
∴当t=时,四边形CPBD面积最大值为.
23.【解答】解:(1)当y=0时,2x﹣3=0,
解得x=,
∴一次函数y=2x﹣3的零点是;
(2)当y=0时,x2+bx+b=0,
∵Δ=b2﹣4×b>0,
∴b>6或b<0,
∴x1+x2=﹣b,x1 x2=b,
∴AB==2,
∴b=3±;
(3)∵直线y=﹣2x+b的零点为1,
∴﹣2+b=0,
解得b=2,
∴y=﹣2x+2,
联立方程组,
整理得kx2﹣(3k+1)x+2k+2=0,
∴xC+xD=,xC xD=,
∴CD==||=|1﹣|,
∵m+1≤≤m+2,
当m+2≤1时,即m≤﹣1,此时CD有最小值|1﹣m﹣2|=3,
解得m=﹣4或m=2(舍);
当m+1≥1时,即m≥0,此时CD有最小值|1﹣m﹣1|=3,
解得m=3或m=﹣3(舍);
当m+1<1<m+2,即﹣1<m<0,此时CD的最小值为0;
综上所述:m的值为3或4.
浙教版2022年九年级上册第1章《二次函数》单元检测卷
满分120分
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)若y=(m﹣1)是二次函数,则m的值是( )
A.1 B.﹣1 C.1或﹣1 D.2
2.(3分)抛物线y=﹣x2+5x﹣3与y轴的交点坐标是( )
A.(0,3) B.(0,﹣3) C.(0,﹣5) D.(0,5)
3.(3分)抛物线y=﹣5(x﹣1)2+2的顶点坐标为( )
A.(﹣1,2) B.(1,﹣2) C.(1,2) D.(2,1)
4.(3分)将二次函数的图象向右平移1个单位,所得图象的解析式为( )
A. B.
C. D.
5.(3分)已知抛物线y=ax2+bx+c过点A(2,3),B(4,3),则该抛物线的对称轴为( )
A.直线x=1 B.直线x=2 C.直线x=3 D.直线x=4
6.(3分)在同一直角坐标系中,一次函数y=ax﹣b和二次函数y=ax2﹣b的图象大致为( )
A.B. C.D.
7.(3分)若抛物线y=ax2﹣x+1与x轴有公共点,则a的取值范围是( )
A.a<且a≠0 B.a≤ C.a≤且a≠0 D.a≥
8.(3分)已知二次函数y=x2﹣4x﹣1,当1<x≤5时,对应的函数值y不可能是( )
A.﹣5 B.﹣4 C.4 D.5
9.(3分)太原某中学利用学校的体育场地设施和设备,充分调动全体师生的积极性,广泛开展各项体育活动,努力提高学生的身体素质,如图①是小杰在铅球比赛中的一次掷球,铅球出手以后的轨迹可近似看作是抛物线的一部分,已知铅球出手时离地面1.6米,铅球离抛掷点水平距离3米时达到最高,此时铅球离地面2.5米,如图②,以水平面为x轴,小杰所站位置的铅垂线为y轴建立平面直角坐标系,则他掷铅球的运动路线的函数表达式为( )
A. B.
C. D.
10.(3分)如图是二次函数y=ax2+bx+c的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a﹣2b+c<0;④若(﹣3,y1),(4,y2)是抛物线上两点,则y1<y2,其中结论正确的是( )
A.①② B.②③④ C.②④ D.①③④
二.填空题(共5小题,满分15分,每小题3分)
11.(3分)在二次函数y=(x﹣1)2+5中,当x>2时,y随x的增大而 (填“增大”或“减小”).
12.(3分)将二次函数化成y=a(x﹣h)2+k的形式,y= .
13.(3分)把y=(3x﹣2)(x+3)化成一般形式后,一次项系数与常数项的和为 .
14.(3分)已知二次函数y=3(x+1)2的图象上有三点A(1,y1),B(2,y2),C(﹣2,y3),则y1,y2,y3的大小关系为 .
15.(3分)设max{x,y}表示x,y两个数中的最大值.例如“max{1,3}=3,max{﹣2,0,}=”.则关于x的函数y=max{2x,﹣x﹣2,﹣x2}的最小值为 .
三.解答题(共8小题,满分75分)
16.(8分)已知抛物线y=﹣x2+2x+2.
(1)写出它的开口方向、对称轴和顶点坐标;
(2)当x为何值时,函数y=﹣x2+2x+2取得最大值,请求出这个最大值.
17.(8分)如图所示,某建筑工地准备利用一面旧墙建一个矩形储料场,新建墙的总长为30米.
(1)当矩形ABCD的长和宽分别为多少时,矩形的面积最大?
(2)若要使矩形的面积为72平方米,长和宽应取多少米?
18.(9分)已知二次函数顶点坐标为(﹣1,4),且抛物线过点(2,﹣5).
(1)求二次函数解析式,并在平面直角坐标系中画出该函数的图象.
(2)已知抛物线y=x2+x﹣6与x轴两个交点分别是A、B(点A在点B的左侧),求A、B的坐标.
(3)利用函数图象,写出y<0时,x的取值范围.
19.(9分)已知,抛物线y=x2+(m﹣1)x+(m﹣2)(m为常数).
(1)求证:无论m为何值,抛物线与x轴总有公共点;
(2)若抛物线的顶点在x轴上,求m的值;
(3)若抛物线与x轴的两个交点之间的距离为4,求m的值.
20.(9分)已知二次函数y=x2﹣2x﹣3的图象与x轴交于A、B两点,与y轴交于点C,求:
(1)点A、B、C的坐标;
(2)△ABC的面积.
21.(10分)某超市经销一种销售成本为每件40元的商品.据市场调查分析,如果按每件50元销售,一周能售出500件;若销售单价每涨1元,每周销售量就减少10件.
(1)当销售单价为52元时,销售量为 件,总利润为 元;
(2)要使得一周的销售利润达到8000元,销售单价应定为多少元?
(3)该超市为了获得最大利润,应将销售单价定为多少元?
22.(10分)如图,在平面直角坐标系中,已知抛物线与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.
(1)求该抛物线的函数表达式;
(2)点P是直线BC下方抛物线上的任意一点,连结PB,PC,以PB,PC为邻边作平行四边形CPBD,求四边形CPBD面积的最大值;
23.(12分)我们将使得函数值为零的自变量的值称为函数的零点.例如,对于函数y=x﹣1,令y=0,可得x=1,我们就说1是函数y=x﹣1的零点.
(1)求一次函数y=2x﹣3的零点;
(2)若二次函数y=x2+bx+b的零点为x1,x2,A,B两点的坐标依次A(x1,0),B(x2,0),如果AB=2,求b的值;
(3)直线y=﹣2x+b的零点为1,且与抛物线y=kx2﹣(3k+3)x+2k+4(k≠0)交于C、D两点,若m+1≤≤m+2时,线段CD有最小值3,求m.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:∵y=(m﹣1)是二次函数,
∴m2+1=2且m﹣1≠0,
解得m=﹣1或m=1(舍),
∴m=﹣1,
故选:B.
2.【解答】解:在y=﹣x2+5x﹣3中,令x=0,得y=﹣3,
∴该抛物线与y轴的交点坐标为(0,﹣3).
故选:B.
3.【解答】解:∵y=﹣5(x﹣1)2+2,
∴此函数的顶点坐标是(1,2).
故选:C.
4.【解答】解:将二次函数的图象向右平移1个单位,所得图象的解析式为:.
故选:A.
5.【解答】解:∵抛物线y=ax2+bx+c过点A(2,3),B(4,3),
∴此两点关于抛物线的对称轴对称,
∴对称轴为直线x==3.
故选:C.
6.【解答】解:A、由一次函数y=ax﹣b的图象可得:a>0,﹣b>0,此时二次函数y=ax2﹣b的图象应该开口向上,故A错误;
B、由一次函数y=ax﹣b的图象可得:a<0,﹣b>0,此时二次函数y=ax2﹣b的图象应该开口向下,故B错误;
C、由一次函数y=ax﹣b的图象可得:a<0,﹣b>0,此时二次函数y=ax2﹣b的图象应该开口向下,故C错误;
D、由一次函数y=ax﹣b的图象可得:a<0,﹣b>0,此时二次函数y=ax2﹣b的图象应该开口向下,顶点的纵坐标﹣b大于零,故D正确;
故选:D.
7.【解答】解:根据题意,得Δ=(﹣1)2﹣4a≥0且a≠0.
解得a≤且a≠0.
故选:C.
8.【解答】解:∵y=x2﹣4x﹣1=(x﹣2)2﹣5,
∴抛物线开口向上,顶点坐标为(2,﹣5),
将x=5代入y=x2﹣4x﹣1得y=4,
∴当1<x≤5时,﹣5≤y≤4,
故选:D.
9.【解答】解:根据题意,得B(0,1.6),C(3,2.5)
设抛物线解析式为y=a(x﹣3)2+2.5,
将B点代入解析式得:9a+2.5=1.6,
解得a=﹣,
∴小杰掷铅球的运动路线的解析式为y=﹣(x﹣3)2+2.5=﹣x2+x+.
故选:A.
10.【解答】解:①∵抛物线开口向下,对称轴为直线x=1,与y轴交于正半轴,
∴a<0,﹣=1,c>0,
∴b=﹣2a>0,
∴abc<0,结论①错误;
②抛物线对称轴为直线x=1,
∴﹣=1,
∴b=﹣2a,
∴2a+b=0,结论②正确;
③∵当x=﹣2时,y<0,
∴4a﹣2b+c<0,结论③正确;
④∵抛物线的对称轴为直线x=1,抛物线开口向下,且1﹣(﹣3)>4﹣1,
∴y1<y2,结论④正确;
综上所述:正确的结论有②③④,
故选:B.
二.填空题(共5小题,满分15分,每小题3分)
11.【解答】解:根据二次函数解析式为y=(x﹣1)2+5,
可知,顶点坐标(1,5),对称轴是直线x=1,
又a=1>0,抛物线开口向上,
所以,当x>2时,y随x的增大而增大.
故答案为:增大.
12.【解答】解:=(x2﹣12x+36﹣36)+21=(x﹣6)2+3,
所以y=(x﹣6)2+3.
故答案为:(x﹣6)2+3.
13.【解答】解:y=(3x﹣2)(x+3)
=3x2+7x﹣6,
其中一次项系数为7,常数项为﹣6,
∴一次项系数与常数项的和为:7+(﹣6)=1,
故答案为:1.
14.【解答】解:由二次函数y=3(x+1)2可知,对称轴为x=﹣1,开口向上,
∵二次函数y=3(x+1)2的图象上有三点A(1,y1),B(2,y2),C(﹣2,y3),
∴C(﹣2,y3)关于对称轴的对称点为(0,y3),
∵﹣1<0<1<2,
∴y3<y1<y2.
故答案为:y3<y1<y2.
15.【解答】解:将y=2x,y=﹣x﹣2和y=﹣x2画在同一个坐标系中,如图所示,
易得点A的坐标为(﹣1,﹣1),点B的坐标为(0,0),
由题意可知,
关于x的函数y=max{2x,﹣x﹣2,﹣x2},即y=2x,y=﹣x﹣2和y=﹣x2的不同范围内的部分图形,
即当x≤﹣1时,y=﹣x﹣2,当x=﹣1时,有最小值,为﹣1;
当﹣1≤x≤0时,y=﹣x2,当x=﹣1时,有最小值,为﹣1;
当x>0时,y=2x,当x=0时,有最小值,为0.
综上关于x的函数y=max{2x,﹣x﹣2,﹣x2}的最小值为﹣1.
三.解答题(共8小题,满分75分)
16.【解答】解:(1)y=﹣x2+2x+2=﹣(x﹣1)2+3,
所以抛物线的开口向下,对称轴为直线x=1,顶点坐标为(1,3);
(2)由(1)可知,当x=1时,函数y=﹣x2+2x+2取得最大值,最大值是3.
17.【解答】解:(1)设AB=x米,则BC=(30﹣2x)米,矩形ABCD的面积为S平方米,
根据题意得:S=x(30﹣2x)=﹣2x2+30x=﹣2(x﹣)2+,
∵﹣2<0,
∴当x=时,S最大,最大值为,
此时30﹣2x=15,
∴矩形ABCD的长为15米,宽为米时,矩形的面积最大;
(2)设AB=x米,则BC=(30﹣2x)米,
根据题意得:x(30﹣2x)=72,
解得:x1=3,x2=12,
当x=3时,30﹣2x=24,
当x=12时,30﹣2x=6,
∵BC>AB,
∴x=3,
答:矩形的长为24米,宽为3米时矩形的面积为72平方米.
18.【解答】解:(1)∵二次函数的图象的顶点坐标为(﹣1,4).
∴设二次函数的解析式为y=a(x+1)2+4,
把(2,﹣5)代入得,﹣5=a(2+1)2+4,
解得a=﹣1,
∴这个函数的解析式为y=﹣(x+1)2+4=﹣x2﹣2x+3,
函数的图象如图:
.
(2)y=x2+x﹣6,令y=0,则x=2或﹣3,
即A(﹣3,0),B(2,0);
(3)由图象可以看出:y<0时,x的取值范围为:x>1或x<﹣3.
19.【解答】(1)证明:令x2+(m﹣1)x+(m﹣2)=0,
则Δ=(m﹣1)2﹣4(m﹣2)=m2﹣2m+1﹣4m+8=m2﹣6m+9=(m﹣3)2,
∵Δ=(m﹣3)2≥0,
∴无论m为何值,抛物线与x轴总有公共点.
(2)解:当抛物线顶点在x轴上时,抛物线与x轴只有1个公共点,
∴(m﹣3)2=0,
∴m=3.
(3)解:∵y=x2+(m﹣1)x+(m﹣2)=(x+m﹣2)(x+1),
∴抛物线与x轴交点坐标为(2﹣m,0),(﹣1,0),
若抛物线与x轴的两个交点之间的距离为4,则2﹣m﹣(﹣1)=4或﹣1﹣(2﹣m)=4,
解得m=﹣1或m=7.
20.【解答】解:(1)令x=0,则y=﹣3,
∴C(0,﹣3);
令y=0,则x2﹣2x﹣3=0,
解得:x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0);
(2)∵A(﹣1,0),B(3,0),C(0,﹣3),
∴AB=4,OC=3,
∴S△ABC=AB OC=×4×3=6.
21.【解答】解:(1)由题意得:当售价为52元时,销售量为500﹣(52﹣50)×10=480(件),
销售利润为(50﹣40)×480=4800(元).
故答案为:480,4800;
(2)设销售单价为x元,一周的销售量为y件,
根据题意题意得:y=500﹣10(x﹣50)=﹣10x+1000,(50≤x≤100),
则(x﹣40)(﹣10x+1000)=8000,
解得x1=60,x2=80,
答:销售单价应定为60元或80元;
(3)设一周利润为w元,
根据题意得:w=(x﹣40)(﹣10x+1000)=﹣10x2+1400x﹣40000=﹣10(x﹣70)2+9000,
∵﹣10<0,
∴当x=70时,w有最大值,最大值为9000,
答:该超市为了获得最大利润,应将销售单价定为70元.
22.【解答】解:(1)将A(﹣1,0),B(3,0)代入,
∴,
解得,
∴y=x2﹣x﹣2;
(2)过P作PE∥y轴交直线BC于点E,
令x=0,则y=﹣2,
∴C(0,﹣2),
设直线BC的解析式为y=kx+b,
,
解得,
∴y=x﹣2,
设P(t,t2﹣t﹣2),则E(t,t﹣2),
∴PE=﹣t2+2t,
∴S△PBC=3(﹣t2+2t)=﹣t2+3t,
∵S平行四边形CPBD=2S△PBC=﹣2t2+6t=﹣2(t﹣)2+,
∴当t=时,四边形CPBD面积最大值为.
23.【解答】解:(1)当y=0时,2x﹣3=0,
解得x=,
∴一次函数y=2x﹣3的零点是;
(2)当y=0时,x2+bx+b=0,
∵Δ=b2﹣4×b>0,
∴b>6或b<0,
∴x1+x2=﹣b,x1 x2=b,
∴AB==2,
∴b=3±;
(3)∵直线y=﹣2x+b的零点为1,
∴﹣2+b=0,
解得b=2,
∴y=﹣2x+2,
联立方程组,
整理得kx2﹣(3k+1)x+2k+2=0,
∴xC+xD=,xC xD=,
∴CD==||=|1﹣|,
∵m+1≤≤m+2,
当m+2≤1时,即m≤﹣1,此时CD有最小值|1﹣m﹣2|=3,
解得m=﹣4或m=2(舍);
当m+1≥1时,即m≥0,此时CD有最小值|1﹣m﹣1|=3,
解得m=3或m=﹣3(舍);
当m+1<1<m+2,即﹣1<m<0,此时CD的最小值为0;
综上所述:m的值为3或4.
同课章节目录
