3.3.1垂径定理 课件(共20张PPT)
文档属性
| 名称 | 3.3.1垂径定理 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-13 10:22:05 | ||
图片预览




文档简介
(共19张PPT)
垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的弧。
初中数学——九年级上册
(1)在透明纸上任意作一个圆和这个圆的任意一条直径CD, 然后沿着直径所在的直线把纸折叠,你发现了什么
结论1:圆是轴对称图形,每一条直径所在的直线都是对称轴。
圆的对称轴有无数条
O
C
D
(2)在刚才操作的基础上,再作一条和直径CD垂直的弦AB,AB与CD相交于点E,然后沿着直径CD所在的直线把纸折叠,你发现哪些点、线互相重合 如果把能够重合的圆弧叫做相等的圆弧(等弧),有哪些圆弧相等?
A
B
E
并且平分弦所对的弧.
结论2:垂直于弦的直径平分这条弦,
自主探究
A
B
E
O
C
D
∴沿CD折叠,点A与点B重合,弧AC和弧BC重合,
弧AD和弧BD重合.
(3)请你对上述命题写出已知,求证,并给出证明.
已知:如图,CD是⊙O的直径,AB是⊙O的一
条弦,CD⊥AB,且交AB于点E.
求证:
EA=EB, AC= BC, AD=BD.
⌒
⌒
⌒
⌒
证明:连结OA,OB.
∵在三角形AOB 中
∠OEA=∠OEB=Rt∠,AO=BO
∴EA=EB(等腰三角形三线合一).
⌒
⌒
⌒
⌒
∴ EA=EB, AC= BC,AD=BD.
思考:你能利用其他方法说明OC平分AB吗?
命题证明
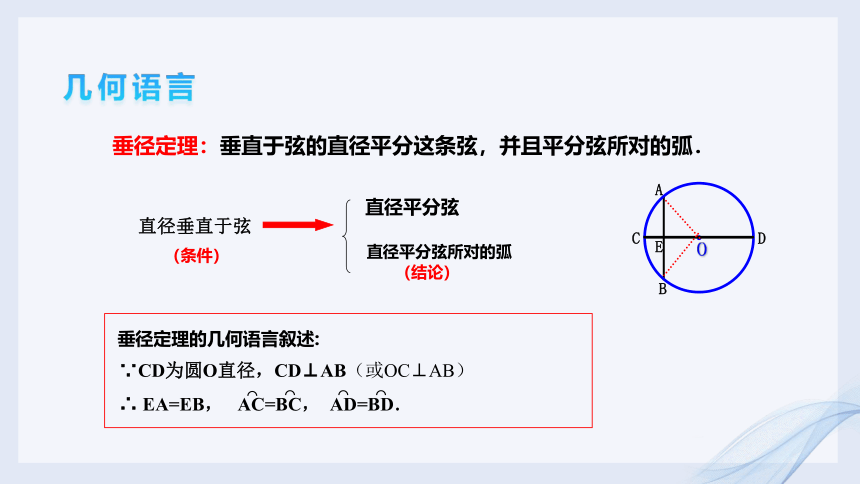
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.
垂径定理的几何语言叙述:
∵CD为圆O直径,CD⊥AB(或OC⊥AB)
∴ EA=EB, AC=BC, AD=BD.
⌒
⌒
⌒
⌒
A
B
O
C
D
E
直径垂直于弦
直径平分弦所对的弧
直径平分弦
(条件)
(结论)
几何语言
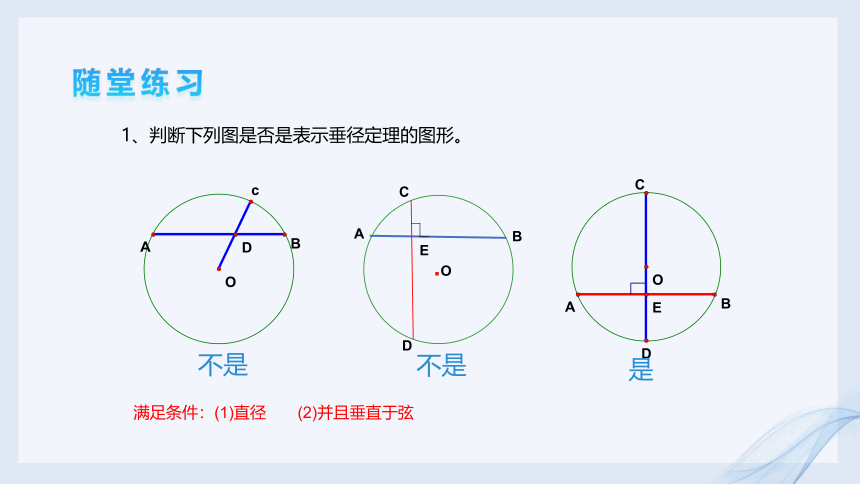
1、判断下列图是否是表示垂径定理的图形。
不是
不是
是
满足条件:(1)直径 (2)并且垂直于弦
随堂练习
C
D
A
B
E
.O
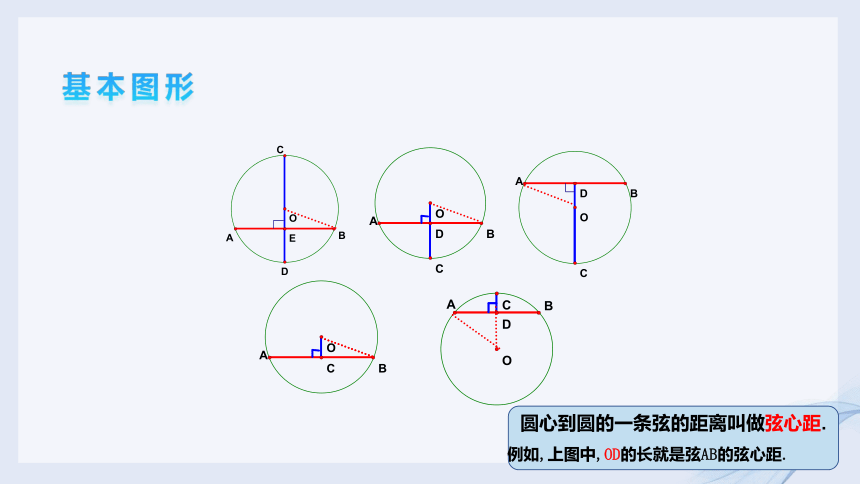
基本图形
圆心到圆的一条弦的距离叫做弦心距.
例如,上图中,OD的长就是弦AB的弦心距.
作法:
⒈ 连结AB.
⒉ 作AB的垂直平分线 CD,交弧AB于点E.
点E就是所求弧AB的中点.
C
D
A
B
E
例1 已知弧AB,如图,用直尺和圆规求作这条弧的中点.
⌒
分析:要平分AB,只要画垂直于弦AB的直径.而这条直径应在弦AB的垂直平分线上.因此画AB的垂直平分线就能把AB平分.
⌒
⌒
思考:你可以确定这个圆的圆心和半径吗?
例题讲解
.O
F
做一做:
1.如图,过已知⊙O内的一点A作弦,使A是该弦
的中点,然后作出弦所对的两条弧的中点.
B
C
BC就是所要求的弦
点D,E就是所要求的弦
所对的两条弧的中点.
D
E
例2 一条排水管的截面如图所示。已知排水管的半径OB=10,水面宽AB=16。求截面圆心O到水面的距离。
D
C
10
8
8
解:作OC⊥AB于C,
由垂径定理得:
AC=BC=1/2AB=0.5×16=8.
由勾股定理得:
想一想:
(1)排水管中水的深度多少
(2)如果水面继续上升,水面的宽度仍然是16,此时水深多少?
答:截面圆心O到水面的距离为6.
例题讲解
题后小结:
1.作弦心距和半径是圆中常见的辅助线;
.
O
A
B
C
r
d
2 .半径(r)、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路,它们之间的关系:
想一想:
在同一个圆中,两条弦的长短与它们所对应的
弦心距之间有什么关系?
答:在同一个圆中,
弦心距越长,所对应的弦就越短;
弦心距越短,所对应的弦就越长.
C
A
B
O
D
.
在直径为20厘米的球形油槽内装入一些油后,截面如
图所示,如果油面宽是16厘米,求油槽中油的深度.
C
D
F
解:
因为OE⊥CD,
过O作OE⊥CD于点E,延长OE交CD于点F,
⌒
O
E
所以油槽中油的深度EF=10-6=4(厘米)
连结OD.
做一做
3、已知:如图,⊙O 中, AB为 弦,OC ⊥AB OC交AB 于D ,AB = 6cm ,CD = 1cm. 求⊙O 的半径.
3
3
1
做一做
同心圆O中,大圆的弦AB与小圆交于C,D
两点,判断线段AC与BD的大小关系,并说明
理由.
AC与BD相等。理由如下:
解:
过点O作OE⊥AB于点E,
则AE=BE,CE=DE,
所以AE-CE=BE-DE,
即AC=BD.
O
C
D
A
B
E
同心圆是指两个
圆的圆心相同
做一做
做一做
5、已知:如图在⊙O中,弦AB//CD。
求证:
AC=BD
⌒
⌒
适度拓展
1、已知⊙O的半径为10cm,点P是⊙O内一点,且OP=8,则过点P的所有弦中,最短的弦是( )
(A)6cm (B)8cm (C)10cm (D)12cm
D
10
8
6
2.如图,⊙O的直径为10,弦AB长为8,M是弦AB上的动点,则OM的长的取值范围是( )
A.3≤OM≤5 B.4≤OM≤5
C.3.
A
B
O
M
适度拓展
A
1.本节课主要内容:(1)圆的轴对称性;(2)垂径定理.
2.垂径定理的应用:(1)作图;(2)计算和证明.
3.解题的主要方法:
(2)半径(r)、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路,它们之间的关系:
(1)画弦心距和半径是圆中常见的辅助线;
课堂小结
作业
(1)完成配套作业本相关练习。
(2)根据垂径定理的基本模型图设计一道例题,并解答。
垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的弧。
初中数学——九年级上册
(1)在透明纸上任意作一个圆和这个圆的任意一条直径CD, 然后沿着直径所在的直线把纸折叠,你发现了什么
结论1:圆是轴对称图形,每一条直径所在的直线都是对称轴。
圆的对称轴有无数条
O
C
D
(2)在刚才操作的基础上,再作一条和直径CD垂直的弦AB,AB与CD相交于点E,然后沿着直径CD所在的直线把纸折叠,你发现哪些点、线互相重合 如果把能够重合的圆弧叫做相等的圆弧(等弧),有哪些圆弧相等?
A
B
E
并且平分弦所对的弧.
结论2:垂直于弦的直径平分这条弦,
自主探究
A
B
E
O
C
D
∴沿CD折叠,点A与点B重合,弧AC和弧BC重合,
弧AD和弧BD重合.
(3)请你对上述命题写出已知,求证,并给出证明.
已知:如图,CD是⊙O的直径,AB是⊙O的一
条弦,CD⊥AB,且交AB于点E.
求证:
EA=EB, AC= BC, AD=BD.
⌒
⌒
⌒
⌒
证明:连结OA,OB.
∵在三角形AOB 中
∠OEA=∠OEB=Rt∠,AO=BO
∴EA=EB(等腰三角形三线合一).
⌒
⌒
⌒
⌒
∴ EA=EB, AC= BC,AD=BD.
思考:你能利用其他方法说明OC平分AB吗?
命题证明
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.
垂径定理的几何语言叙述:
∵CD为圆O直径,CD⊥AB(或OC⊥AB)
∴ EA=EB, AC=BC, AD=BD.
⌒
⌒
⌒
⌒
A
B
O
C
D
E
直径垂直于弦
直径平分弦所对的弧
直径平分弦
(条件)
(结论)
几何语言
1、判断下列图是否是表示垂径定理的图形。
不是
不是
是
满足条件:(1)直径 (2)并且垂直于弦
随堂练习
C
D
A
B
E
.O
基本图形
圆心到圆的一条弦的距离叫做弦心距.
例如,上图中,OD的长就是弦AB的弦心距.
作法:
⒈ 连结AB.
⒉ 作AB的垂直平分线 CD,交弧AB于点E.
点E就是所求弧AB的中点.
C
D
A
B
E
例1 已知弧AB,如图,用直尺和圆规求作这条弧的中点.
⌒
分析:要平分AB,只要画垂直于弦AB的直径.而这条直径应在弦AB的垂直平分线上.因此画AB的垂直平分线就能把AB平分.
⌒
⌒
思考:你可以确定这个圆的圆心和半径吗?
例题讲解
.O
F
做一做:
1.如图,过已知⊙O内的一点A作弦,使A是该弦
的中点,然后作出弦所对的两条弧的中点.
B
C
BC就是所要求的弦
点D,E就是所要求的弦
所对的两条弧的中点.
D
E
例2 一条排水管的截面如图所示。已知排水管的半径OB=10,水面宽AB=16。求截面圆心O到水面的距离。
D
C
10
8
8
解:作OC⊥AB于C,
由垂径定理得:
AC=BC=1/2AB=0.5×16=8.
由勾股定理得:
想一想:
(1)排水管中水的深度多少
(2)如果水面继续上升,水面的宽度仍然是16,此时水深多少?
答:截面圆心O到水面的距离为6.
例题讲解
题后小结:
1.作弦心距和半径是圆中常见的辅助线;
.
O
A
B
C
r
d
2 .半径(r)、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路,它们之间的关系:
想一想:
在同一个圆中,两条弦的长短与它们所对应的
弦心距之间有什么关系?
答:在同一个圆中,
弦心距越长,所对应的弦就越短;
弦心距越短,所对应的弦就越长.
C
A
B
O
D
.
在直径为20厘米的球形油槽内装入一些油后,截面如
图所示,如果油面宽是16厘米,求油槽中油的深度.
C
D
F
解:
因为OE⊥CD,
过O作OE⊥CD于点E,延长OE交CD于点F,
⌒
O
E
所以油槽中油的深度EF=10-6=4(厘米)
连结OD.
做一做
3、已知:如图,⊙O 中, AB为 弦,OC ⊥AB OC交AB 于D ,AB = 6cm ,CD = 1cm. 求⊙O 的半径.
3
3
1
做一做
同心圆O中,大圆的弦AB与小圆交于C,D
两点,判断线段AC与BD的大小关系,并说明
理由.
AC与BD相等。理由如下:
解:
过点O作OE⊥AB于点E,
则AE=BE,CE=DE,
所以AE-CE=BE-DE,
即AC=BD.
O
C
D
A
B
E
同心圆是指两个
圆的圆心相同
做一做
做一做
5、已知:如图在⊙O中,弦AB//CD。
求证:
AC=BD
⌒
⌒
适度拓展
1、已知⊙O的半径为10cm,点P是⊙O内一点,且OP=8,则过点P的所有弦中,最短的弦是( )
(A)6cm (B)8cm (C)10cm (D)12cm
D
10
8
6
2.如图,⊙O的直径为10,弦AB长为8,M是弦AB上的动点,则OM的长的取值范围是( )
A.3≤OM≤5 B.4≤OM≤5
C.3
A
B
O
M
适度拓展
A
1.本节课主要内容:(1)圆的轴对称性;(2)垂径定理.
2.垂径定理的应用:(1)作图;(2)计算和证明.
3.解题的主要方法:
(2)半径(r)、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路,它们之间的关系:
(1)画弦心距和半径是圆中常见的辅助线;
课堂小结
作业
(1)完成配套作业本相关练习。
(2)根据垂径定理的基本模型图设计一道例题,并解答。
同课章节目录
