第一章 三角形的初步认识 章末复习(二) 课件(共36张PPT)
文档属性
| 名称 | 第一章 三角形的初步认识 章末复习(二) 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-14 10:27:13 | ||
图片预览






文档简介
(共36张PPT)
第一章 三角形的初步认识
浙教版 八年级上册
要点梳理
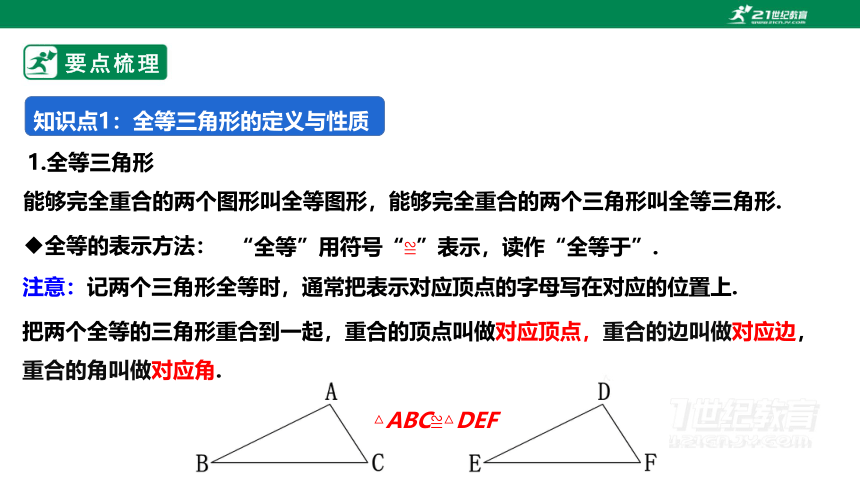
能够完全重合的两个图形叫全等图形,能够完全重合的两个三角形叫全等三角形.
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
1.全等三角形
△ABC≌△DEF
全等的表示方法:
“全等”用符号“≌”表示,读作“全等于”.
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
知识点1:全等三角形的定义与性质
要点梳理
2.全等三角形的性质
全等三角形的对应边相等,全等三角形的对应角相等.
几何语言:
∵ △ABC≌△A1B1C1
∴ AB=A1B1,AC=A1C1,BC=B1C1,∠A=∠A1,∠B=∠B1,∠C=∠C1
考点讲练
例1 如图,已知△ABC≌△DEB,E为AB的中点,AC与BD交于点F,DE=10,
∠C=55°,∠D=25°.
(1)求BC的长;
(2)求∠CBF的度数.
解:(1)∵△ABC≌△DEB,
∴AB=DE=10,BC=BE.
∵E为AB的中点,∴BE=AB=5,∴BC=5.
考点1 全等三角形的性质
考点讲练
例1 如图,已知△ABC≌△DEB,E为AB的中点,AC与BD交于点F,DE=10,
∠C=55°,∠D=25°.
(1)求BC的长;
(2)求∠CBF的度数.
(2)∵△ABC≌△DEB,∠C=55°,∠D=25°,
∴∠A=∠D=25°,∠DBE=∠C=55°,
∴∠ABC=180°-∠A-∠C=180°-25°-55°=100°,
∴∠CBF=∠ABC-∠DBE=100°-55°=45°.
考点讲练
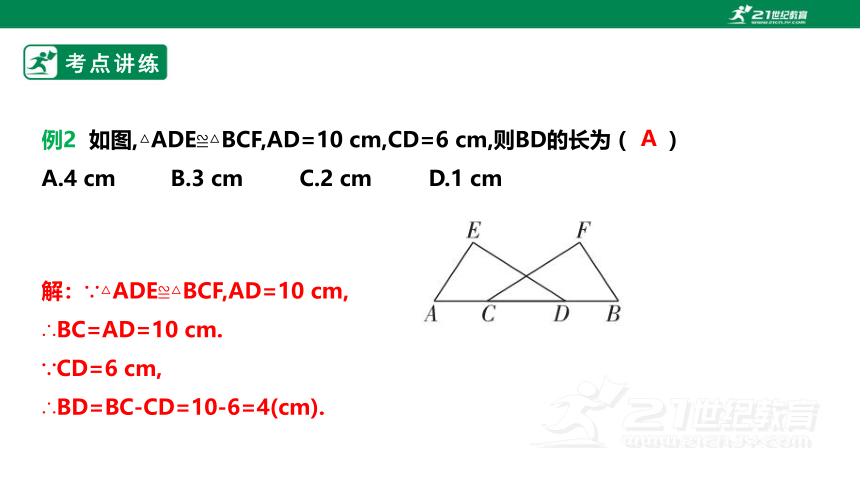
例2 如图,△ADE≌△BCF,AD=10 cm,CD=6 cm,则BD的长为 ( )
A.4 cm B.3 cm C.2 cm D.1 cm
解:∵△ADE≌△BCF,AD=10 cm,
∴BC=AD=10 cm.
∵CD=6 cm,
∴BD=BC-CD=10-6=4(cm).
A
考点讲练
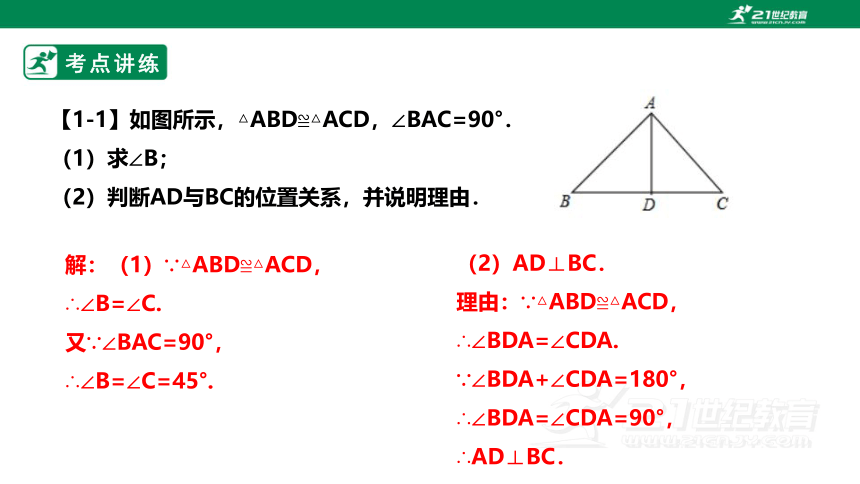
【1-1】如图所示,△ABD≌△ACD,∠BAC=90°.
(1)求∠B;
(2)判断AD与BC的位置关系,并说明理由.
解:(1)∵△ABD≌△ACD,
∴∠B=∠C.
又∵∠BAC=90°,
∴∠B=∠C=45°.
(2)AD⊥BC.
理由:∵△ABD≌△ACD,
∴∠BDA=∠CDA.
∵∠BDA+∠CDA=180°,
∴∠BDA=∠CDA=90°,
∴AD⊥BC.
考点讲练
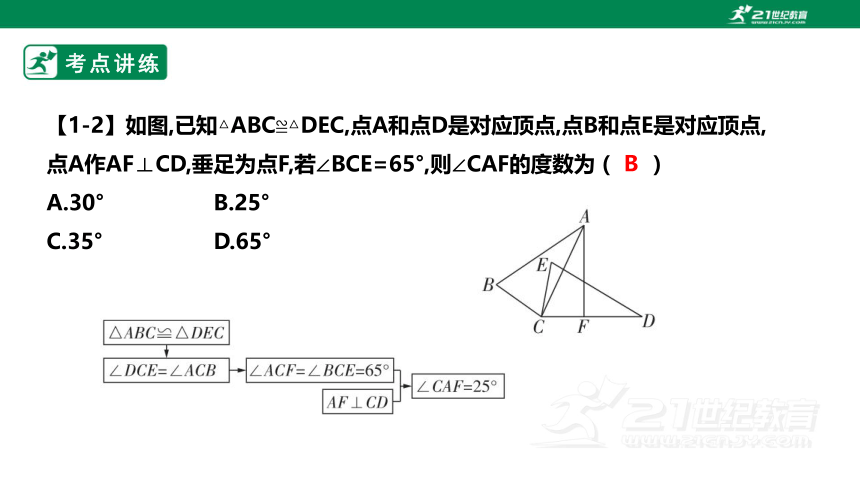
【1-2】如图,已知△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点, 点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为 ( )
A.30° B.25°
C.35° D.65°
B
要点梳理
文字语言:三边对应相等的两个三角形全等.(简写为“边边边”或“SSS”)
“边边边”判定方法
在△ABC和△A′B′C′中,
∴△ABC≌△ A′B′C′ (SSS).
AB=A′B′,
BC=B′C′,
CA=C′A′,
几何语言:
知识点2:三角形全等的判定方法
要点梳理
证明两个三角形全等的书写步骤:
①准备条件:证全等时要用的条件要先证好;
②指明范围:写出在哪两个三角形中;
③摆齐根据:摆出三个条件用大括号括起来;
④写出结论:写出全等结论.
要点梳理
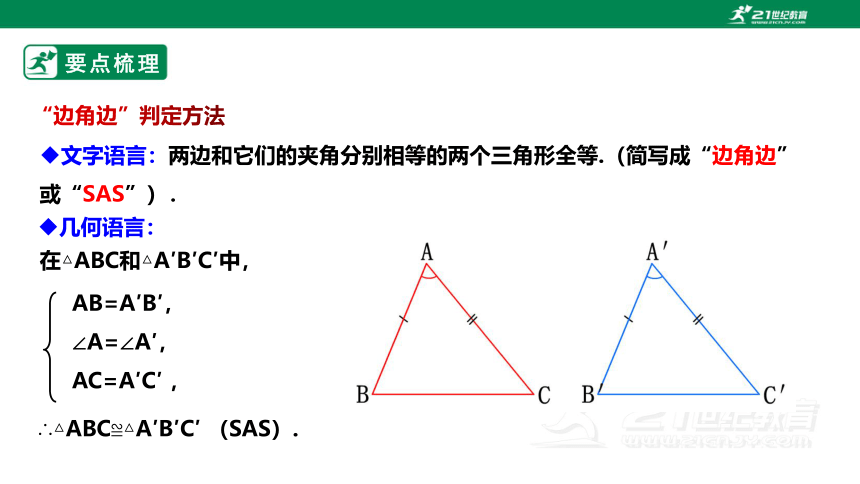
文字语言:两边和它们的夹角分别相等的两个三角形全等.(简写成“边角边”或“SAS”).
“边角边”判定方法
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′ (SAS).
AB=A′B′,
∠A=∠A′,
AC=A′C′ ,
几何语言:
要点梳理
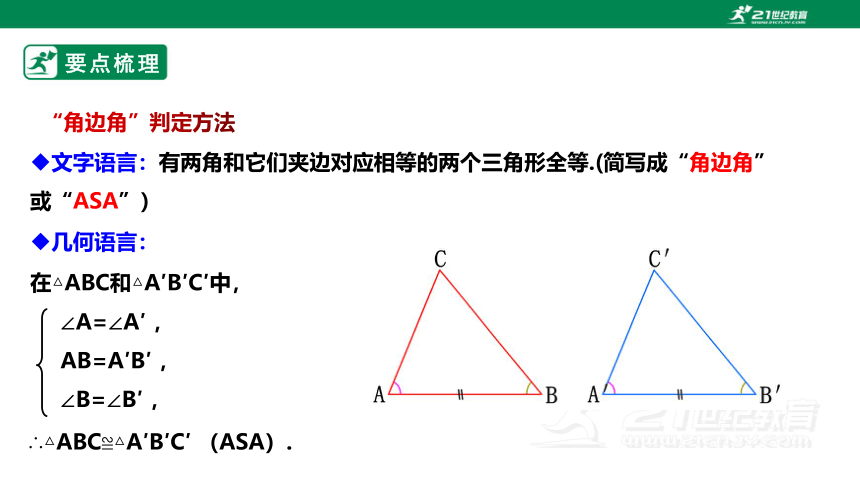
文字语言:有两角和它们夹边对应相等的两个三角形全等.(简写成“角边角”或“ASA”)
“角边角”判定方法
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′ (ASA).
∠A=∠A′ ,
AB=A′B′ ,
∠B=∠B′ ,
几何语言:
要点梳理
◆文字语言:两角分别相等且其中一组等角的对边相等的两个三角形全等.
(可以简写成“角角边”或“AAS”).
“角角边”判定方法:
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′ (ASA).
∠A=∠A′ ,
∠B=∠B′ ,
BC=B′C′ ,
几何语言:
考点讲练
例3 已知,∠ABC=∠DCB,∠ACB= ∠DBC,
求证:△ABC≌△DCB.
∠ABC=∠DCB,
BC=CB,
∠ACB=∠DBC,
证明:
在△ABC和△DCB中,
∴△ABC≌△DCB(ASA ).
B
C
A
D
分析:运用“两角和它们的夹边对应相等两个三角形全等”进行判定.
考点2 三角形全等的判定方法
考点讲练
例4 如图,点P是AB上任意一点,∠ABC=∠ABD,还应补充一个条件,才能推出△APC≌△APD.从下列条件中补充一个条件,不一定能推出△APC≌△APD的是( )
A.BC=BD; B.AC=AD;
C.∠ACB=∠ADB; D.∠CAB=∠DAB
B
考点讲练
例5 如图AB=AD,AC=AE,∠BAE=∠DAC.
求证:(1)∠C=∠E;(2)AM=AN.
证明:(1)∵∠BAE=∠DAC,
∴∠BAC=∠DAE ,
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS)
∴∠C=∠E.
考点讲练
例5 如图AB=AD,AC=AE,∠BAE=∠DAC.
求证:(1)∠C=∠E;(2)AM=AN.
(2)∵△ABC≌△ADE
∴∠B=∠D
在△ABM和△ADN中,
∴△ABM≌△AND(ASA)
∴AM=AN.
考点讲练
例6 如图,点A,B分别在OC,OD上,AD与BC相交于点E,∠C=∠D,DE=EC,则下列结论不一定正确的是 ( )
A.AD=BC B.OA=AC
C.∠OAD=∠OBC D.△OAD≌△OBC
解:在△DEB和△CEA中,
∴△DEB≌△CEA(ASA),∴BE=AE,
∴AD=BC.在△OAD和△OBC中,
B
∴△OAD≌△OBC(AAS),
∴∠OAD=∠OBC,OA=OB.根据题中条件无法得到OA=AC,故B不一定正确.
考点讲练
例7 如图,E,F是BD上两点,AB=CD,BF=DE,AE=CF.求证:AC与BD互相平分.
证明:∵BF=DE,
∴BF-EF=DE-EF,即BE=DF.
在△ABE和△CDF中,
∴△ABE≌△CDF(SSS),∴∠B=∠D.
在△ABO和△CDO中,
∴△ABO≌△CDO(AAS),
∴OA=OC,OB=OD,
∴AC与BD互相平分.
考点讲练
【2-1】已知△ABC和△DEF,下列条件中,不能保证△ABC和△DEF全等的是( )
A.AB=DE,AC=DF,BC=EF
B. ∠A= ∠ D, ∠ B= ∠ E,AC=DF
C.AB=DE,AC=DF, ∠A= ∠D
D.AB=DE,BC=EF, ∠ C= ∠ F
D
考点讲练
【2-2】如图,已知CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD交于点0,且AO平分∠BAC,那么图中全等三角形共有______对.
4
【分析】根据条件: CD⊥AB,BE⊥AC ,AO平分∠BAC及隐含的条件AO=AO(公共边).
∴△ADO≌△AEO(AAS),∴AD=AE,
∴△ADC≌△AEB(ASA),∴∠B=∠C,
∴△ABO≌△ACO(AAS),∴BO=CO,∴△BDO≌△CEO(AAS),
∴图中全等三角形共有4对.
考点讲练
【2-3】如图:在ΔABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG.
(1)求证:∠ABE=∠ACG;
(2)试判:AG与AD的关系?并说明理由.
(1)证明:∵BE、CF分别是AC、AB两边上的高,
∴∠AFC=∠AEB=90°,
∴∠ACG+∠FAC=∠FAC+∠ABE=90°,
∴∠ABE=∠ACG;
(2)解:AG=AD,AG⊥AD,理由如下:
由(1)可知:∠ABD=∠GCA,
∵BD=AC,AB=GC,
∴△ABD≌△GCA(SAS),
∴AG=AD,∠BAD=∠CGA,
∵∠AFG=90°,
∴∠CGA+∠GAF=90°,
∴∠BAD+∠GAF=90°,即∠GAD=90°,
∴AG⊥AD.
考点讲练
【2-4】如图,在四边形ABCD中,∠ABC=90°,AD∥BC,以B为圆心,BC长为半径画弧,与AD相交于点E,连接BE, 点C作CF⊥BE,
垂足为F.若AE=8,BC=10,则EF的长为 .
解:因为∠ABC=90°,AD∥BC,所以∠A=180°-∠ABC=90°,∠AEB=∠FBC.因为CF⊥BE,所以∠BFC=90°,所以∠A=∠BFC.在△AEB和△FBC中,所以△AEB≌△FBC(AAS),所以BF=AE=8,所以EF=BE-BF=10-8=2.
2
要点梳理
垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线.
A
B
D
l
如图,直线l⊥AB于点D,且AD=BD,直线l就是线段AB的垂直平分线.
结论:线段垂直平分线上的点到线段两端的距离相等.
线段垂直平分线的性质:
知识点3:垂直平分线的性质
考点讲练
例8 如图,线段AC的垂直平分线交线段AB于点D,∠A=50°,则∠BDC等于( )
A.50° B.100°
C.120° D.130°
B
考点3 垂直平分线的性质
考点讲练
例9 如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19 cm,△ABD的周长为13 cm,则AE的长为( )
A.3 cm B.6 cm C.12 cm D.16 cm
A
要点梳理
文字语言:角平分线上的点到角的两边的距离相等.
角平分线的性质
几何语言:
∵点P在∠AOB的平分线上,且PD⊥OA,PE⊥OB.
∴PD=PE
P到OA的距离
P到OB的距离
角平分线上的点
知识点4:角平分线的性质
考点讲练
例10 如图,P为∠AOB平分线上的点,PD⊥OA于点D,PD=3 cm,则点P到OB的距离为 ( )
A.5 cm B.4 cm C.3 cm D.2 cm
解:如图, 点P作PE⊥OB于点E,
∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,
∴PE=PD=3 cm.
C
考点4 角平分线的性质
考点讲练
例11 如图,在△ABC中,AB=8,AC=6,AD是角平分线,DE⊥AB,DF⊥AC,
则S△ABD∶S△ACD= ( )
A.4∶3 B.9∶8 C.9∶7 D.3∶2
解:∵AD是角平分线,DE⊥AB,DF⊥AC,∴DE=DF.
∵AB=8,AC=6,S△ABD=AB·DE,S△ACD=AC·DF,
∴S△ABD∶S△ACD=AB∶AC=8∶6=4∶3.
A
考点讲练
【4-1】如图,已知△ABC的周长是20,BO,CO分别平分∠ABC,∠ACB,
OD⊥BC于点D,且OD=3,则△ABC的面积是 ( )
A.20 B.25 C.30 D.35
解:如图,连接OA, 点O作OE⊥AB于点E,OF⊥AC于点F,∵BO,CO分别平分∠ABC,∠ACB,∴OE=OF=OD=3.
∵△ABC的周长是20,∴AB+BC+AC=20,
∴S△ABC=S△ABO+S△BCO+S△ACO=AB×OE+BC×OD+AC×OF
=(AB+BC+AC)×3=×20×3=30.
C
要点梳理
在几何作图中,我们把用没有刻度的直尺和圆规作图,
简称尺规作图。
知识点5:尺规作图
要点梳理
常用的作图语言:
(1)过点×、×作线段或射线、直线;
(2)连结两点×、×;
(3)在线段或射线×上截取××=××;
(4)以点×为圆心,以××的长为半径作圆(或画弧),交××于点×;
(5)分别以点×,点×为圆心,以××,××的长为半径作弧,两弧相交于点×;
(6)延长××到点×,使××=××.
考点讲练
例12 用直尺和圆规作一个角等于已知角,如图,能得出∠A'O'B'=∠AOB的依据是 .
解:由作图知在△C'O'D'和△COD中,O'C'=OC,O'D'=OD,C'D'=CD,
所以△C'O'D'≌△COD(SSS),
所以∠A'O'B'=∠AOB.
SSS
考点5 尺规作图
考点讲练
例13 如图,已知∠AOB,C是OB边上一点, 点C作OA的平行线.(尺规作图,不写作法,保留作图痕迹)
解:如图,以CB为一边,在∠AOB内部作∠BCD=∠BOA,则CD∥OA.
(或以OC为一边,在∠AOB外部作∠OCE=∠AOB,则CE∥OA)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第一章 三角形的初步认识
浙教版 八年级上册
要点梳理
能够完全重合的两个图形叫全等图形,能够完全重合的两个三角形叫全等三角形.
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
1.全等三角形
△ABC≌△DEF
全等的表示方法:
“全等”用符号“≌”表示,读作“全等于”.
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
知识点1:全等三角形的定义与性质
要点梳理
2.全等三角形的性质
全等三角形的对应边相等,全等三角形的对应角相等.
几何语言:
∵ △ABC≌△A1B1C1
∴ AB=A1B1,AC=A1C1,BC=B1C1,∠A=∠A1,∠B=∠B1,∠C=∠C1
考点讲练
例1 如图,已知△ABC≌△DEB,E为AB的中点,AC与BD交于点F,DE=10,
∠C=55°,∠D=25°.
(1)求BC的长;
(2)求∠CBF的度数.
解:(1)∵△ABC≌△DEB,
∴AB=DE=10,BC=BE.
∵E为AB的中点,∴BE=AB=5,∴BC=5.
考点1 全等三角形的性质
考点讲练
例1 如图,已知△ABC≌△DEB,E为AB的中点,AC与BD交于点F,DE=10,
∠C=55°,∠D=25°.
(1)求BC的长;
(2)求∠CBF的度数.
(2)∵△ABC≌△DEB,∠C=55°,∠D=25°,
∴∠A=∠D=25°,∠DBE=∠C=55°,
∴∠ABC=180°-∠A-∠C=180°-25°-55°=100°,
∴∠CBF=∠ABC-∠DBE=100°-55°=45°.
考点讲练
例2 如图,△ADE≌△BCF,AD=10 cm,CD=6 cm,则BD的长为 ( )
A.4 cm B.3 cm C.2 cm D.1 cm
解:∵△ADE≌△BCF,AD=10 cm,
∴BC=AD=10 cm.
∵CD=6 cm,
∴BD=BC-CD=10-6=4(cm).
A
考点讲练
【1-1】如图所示,△ABD≌△ACD,∠BAC=90°.
(1)求∠B;
(2)判断AD与BC的位置关系,并说明理由.
解:(1)∵△ABD≌△ACD,
∴∠B=∠C.
又∵∠BAC=90°,
∴∠B=∠C=45°.
(2)AD⊥BC.
理由:∵△ABD≌△ACD,
∴∠BDA=∠CDA.
∵∠BDA+∠CDA=180°,
∴∠BDA=∠CDA=90°,
∴AD⊥BC.
考点讲练
【1-2】如图,已知△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点, 点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为 ( )
A.30° B.25°
C.35° D.65°
B
要点梳理
文字语言:三边对应相等的两个三角形全等.(简写为“边边边”或“SSS”)
“边边边”判定方法
在△ABC和△A′B′C′中,
∴△ABC≌△ A′B′C′ (SSS).
AB=A′B′,
BC=B′C′,
CA=C′A′,
几何语言:
知识点2:三角形全等的判定方法
要点梳理
证明两个三角形全等的书写步骤:
①准备条件:证全等时要用的条件要先证好;
②指明范围:写出在哪两个三角形中;
③摆齐根据:摆出三个条件用大括号括起来;
④写出结论:写出全等结论.
要点梳理
文字语言:两边和它们的夹角分别相等的两个三角形全等.(简写成“边角边”或“SAS”).
“边角边”判定方法
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′ (SAS).
AB=A′B′,
∠A=∠A′,
AC=A′C′ ,
几何语言:
要点梳理
文字语言:有两角和它们夹边对应相等的两个三角形全等.(简写成“角边角”或“ASA”)
“角边角”判定方法
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′ (ASA).
∠A=∠A′ ,
AB=A′B′ ,
∠B=∠B′ ,
几何语言:
要点梳理
◆文字语言:两角分别相等且其中一组等角的对边相等的两个三角形全等.
(可以简写成“角角边”或“AAS”).
“角角边”判定方法:
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′ (ASA).
∠A=∠A′ ,
∠B=∠B′ ,
BC=B′C′ ,
几何语言:
考点讲练
例3 已知,∠ABC=∠DCB,∠ACB= ∠DBC,
求证:△ABC≌△DCB.
∠ABC=∠DCB,
BC=CB,
∠ACB=∠DBC,
证明:
在△ABC和△DCB中,
∴△ABC≌△DCB(ASA ).
B
C
A
D
分析:运用“两角和它们的夹边对应相等两个三角形全等”进行判定.
考点2 三角形全等的判定方法
考点讲练
例4 如图,点P是AB上任意一点,∠ABC=∠ABD,还应补充一个条件,才能推出△APC≌△APD.从下列条件中补充一个条件,不一定能推出△APC≌△APD的是( )
A.BC=BD; B.AC=AD;
C.∠ACB=∠ADB; D.∠CAB=∠DAB
B
考点讲练
例5 如图AB=AD,AC=AE,∠BAE=∠DAC.
求证:(1)∠C=∠E;(2)AM=AN.
证明:(1)∵∠BAE=∠DAC,
∴∠BAC=∠DAE ,
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS)
∴∠C=∠E.
考点讲练
例5 如图AB=AD,AC=AE,∠BAE=∠DAC.
求证:(1)∠C=∠E;(2)AM=AN.
(2)∵△ABC≌△ADE
∴∠B=∠D
在△ABM和△ADN中,
∴△ABM≌△AND(ASA)
∴AM=AN.
考点讲练
例6 如图,点A,B分别在OC,OD上,AD与BC相交于点E,∠C=∠D,DE=EC,则下列结论不一定正确的是 ( )
A.AD=BC B.OA=AC
C.∠OAD=∠OBC D.△OAD≌△OBC
解:在△DEB和△CEA中,
∴△DEB≌△CEA(ASA),∴BE=AE,
∴AD=BC.在△OAD和△OBC中,
B
∴△OAD≌△OBC(AAS),
∴∠OAD=∠OBC,OA=OB.根据题中条件无法得到OA=AC,故B不一定正确.
考点讲练
例7 如图,E,F是BD上两点,AB=CD,BF=DE,AE=CF.求证:AC与BD互相平分.
证明:∵BF=DE,
∴BF-EF=DE-EF,即BE=DF.
在△ABE和△CDF中,
∴△ABE≌△CDF(SSS),∴∠B=∠D.
在△ABO和△CDO中,
∴△ABO≌△CDO(AAS),
∴OA=OC,OB=OD,
∴AC与BD互相平分.
考点讲练
【2-1】已知△ABC和△DEF,下列条件中,不能保证△ABC和△DEF全等的是( )
A.AB=DE,AC=DF,BC=EF
B. ∠A= ∠ D, ∠ B= ∠ E,AC=DF
C.AB=DE,AC=DF, ∠A= ∠D
D.AB=DE,BC=EF, ∠ C= ∠ F
D
考点讲练
【2-2】如图,已知CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD交于点0,且AO平分∠BAC,那么图中全等三角形共有______对.
4
【分析】根据条件: CD⊥AB,BE⊥AC ,AO平分∠BAC及隐含的条件AO=AO(公共边).
∴△ADO≌△AEO(AAS),∴AD=AE,
∴△ADC≌△AEB(ASA),∴∠B=∠C,
∴△ABO≌△ACO(AAS),∴BO=CO,∴△BDO≌△CEO(AAS),
∴图中全等三角形共有4对.
考点讲练
【2-3】如图:在ΔABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG.
(1)求证:∠ABE=∠ACG;
(2)试判:AG与AD的关系?并说明理由.
(1)证明:∵BE、CF分别是AC、AB两边上的高,
∴∠AFC=∠AEB=90°,
∴∠ACG+∠FAC=∠FAC+∠ABE=90°,
∴∠ABE=∠ACG;
(2)解:AG=AD,AG⊥AD,理由如下:
由(1)可知:∠ABD=∠GCA,
∵BD=AC,AB=GC,
∴△ABD≌△GCA(SAS),
∴AG=AD,∠BAD=∠CGA,
∵∠AFG=90°,
∴∠CGA+∠GAF=90°,
∴∠BAD+∠GAF=90°,即∠GAD=90°,
∴AG⊥AD.
考点讲练
【2-4】如图,在四边形ABCD中,∠ABC=90°,AD∥BC,以B为圆心,BC长为半径画弧,与AD相交于点E,连接BE, 点C作CF⊥BE,
垂足为F.若AE=8,BC=10,则EF的长为 .
解:因为∠ABC=90°,AD∥BC,所以∠A=180°-∠ABC=90°,∠AEB=∠FBC.因为CF⊥BE,所以∠BFC=90°,所以∠A=∠BFC.在△AEB和△FBC中,所以△AEB≌△FBC(AAS),所以BF=AE=8,所以EF=BE-BF=10-8=2.
2
要点梳理
垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线.
A
B
D
l
如图,直线l⊥AB于点D,且AD=BD,直线l就是线段AB的垂直平分线.
结论:线段垂直平分线上的点到线段两端的距离相等.
线段垂直平分线的性质:
知识点3:垂直平分线的性质
考点讲练
例8 如图,线段AC的垂直平分线交线段AB于点D,∠A=50°,则∠BDC等于( )
A.50° B.100°
C.120° D.130°
B
考点3 垂直平分线的性质
考点讲练
例9 如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19 cm,△ABD的周长为13 cm,则AE的长为( )
A.3 cm B.6 cm C.12 cm D.16 cm
A
要点梳理
文字语言:角平分线上的点到角的两边的距离相等.
角平分线的性质
几何语言:
∵点P在∠AOB的平分线上,且PD⊥OA,PE⊥OB.
∴PD=PE
P到OA的距离
P到OB的距离
角平分线上的点
知识点4:角平分线的性质
考点讲练
例10 如图,P为∠AOB平分线上的点,PD⊥OA于点D,PD=3 cm,则点P到OB的距离为 ( )
A.5 cm B.4 cm C.3 cm D.2 cm
解:如图, 点P作PE⊥OB于点E,
∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,
∴PE=PD=3 cm.
C
考点4 角平分线的性质
考点讲练
例11 如图,在△ABC中,AB=8,AC=6,AD是角平分线,DE⊥AB,DF⊥AC,
则S△ABD∶S△ACD= ( )
A.4∶3 B.9∶8 C.9∶7 D.3∶2
解:∵AD是角平分线,DE⊥AB,DF⊥AC,∴DE=DF.
∵AB=8,AC=6,S△ABD=AB·DE,S△ACD=AC·DF,
∴S△ABD∶S△ACD=AB∶AC=8∶6=4∶3.
A
考点讲练
【4-1】如图,已知△ABC的周长是20,BO,CO分别平分∠ABC,∠ACB,
OD⊥BC于点D,且OD=3,则△ABC的面积是 ( )
A.20 B.25 C.30 D.35
解:如图,连接OA, 点O作OE⊥AB于点E,OF⊥AC于点F,∵BO,CO分别平分∠ABC,∠ACB,∴OE=OF=OD=3.
∵△ABC的周长是20,∴AB+BC+AC=20,
∴S△ABC=S△ABO+S△BCO+S△ACO=AB×OE+BC×OD+AC×OF
=(AB+BC+AC)×3=×20×3=30.
C
要点梳理
在几何作图中,我们把用没有刻度的直尺和圆规作图,
简称尺规作图。
知识点5:尺规作图
要点梳理
常用的作图语言:
(1)过点×、×作线段或射线、直线;
(2)连结两点×、×;
(3)在线段或射线×上截取××=××;
(4)以点×为圆心,以××的长为半径作圆(或画弧),交××于点×;
(5)分别以点×,点×为圆心,以××,××的长为半径作弧,两弧相交于点×;
(6)延长××到点×,使××=××.
考点讲练
例12 用直尺和圆规作一个角等于已知角,如图,能得出∠A'O'B'=∠AOB的依据是 .
解:由作图知在△C'O'D'和△COD中,O'C'=OC,O'D'=OD,C'D'=CD,
所以△C'O'D'≌△COD(SSS),
所以∠A'O'B'=∠AOB.
SSS
考点5 尺规作图
考点讲练
例13 如图,已知∠AOB,C是OB边上一点, 点C作OA的平行线.(尺规作图,不写作法,保留作图痕迹)
解:如图,以CB为一边,在∠AOB内部作∠BCD=∠BOA,则CD∥OA.
(或以OC为一边,在∠AOB外部作∠OCE=∠AOB,则CE∥OA)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
