2022年秋浙教版初一第三单元《实数》单元测试卷(含答案)
文档属性
| 名称 | 2022年秋浙教版初一第三单元《实数》单元测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 41.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-14 13:32:17 | ||
图片预览



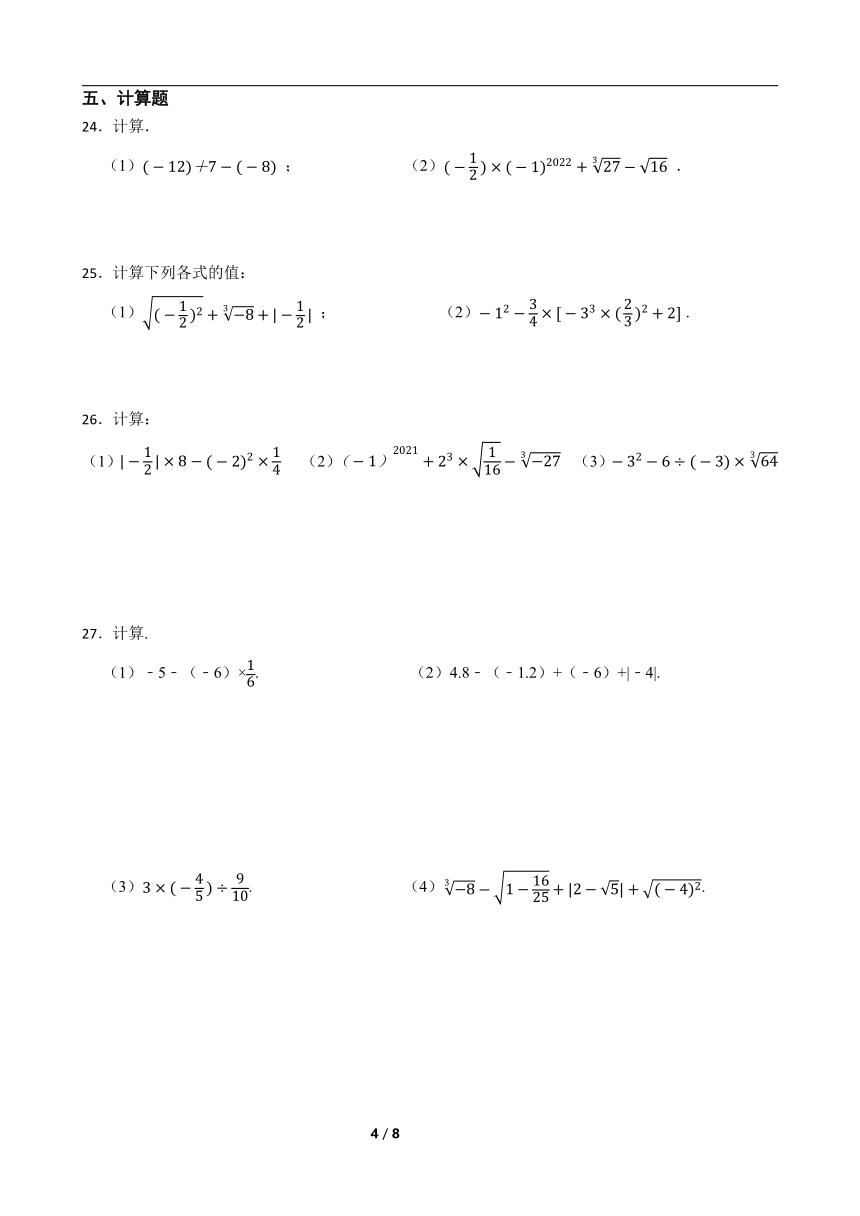
文档简介
初一数学复习讲义
一、单选题
1.在实数 中, 无理数有( )个
A.1 B.2 C.3 D.4
2.在实数:,,,,,,中,无理数有( )
A.1个 B.2个 C.3个 D.4个
3.如图,在Rt△OBC中,OC=1,OB=2,数轴上点A所表示的数为a,则a的值是( )
A.- -2 B.-
C. ﹣2 D.﹣ +2
4.在实数|-3.14|,-3,- ,π中,最小的数是( )
A.- B.-3 C.|-3.14| D.π
5.在数轴上有三个互不重合的点A,B,C,它们代表的实数分别为a,b,c,下列结论中①若abc 0,则A,B,C三点中,至少有一个点在原点右侧;②若a+b+c=0,则A,B,C三点中,至少有一个点在原点右侧;③若a+c=2b,则点B为线段AC的中点;④O为坐标原点且A,B,C均不与O重合,若OB﹣OC=AB﹣AC,则bc 0,
所有正确结论的序号是( )
A.①② B.③④ C.①②③ D.①②③④
6.已知 , , 表示取三个数中最小的那个数﹒例如:当 , , , = , , =3﹒当 , , = 时,则 的值为( )
A. B. C. D.
7.数轴上A,B,C三点所代表的数分别是a、b、2,且 .下列四个选项中,有( )个能表示A,B,C三点在数轴上的位置关系.
①②③④
A.1个 B.2个 C.3个 D.4个
8.若6- 的整数部分为x,小数部分为y,则(2x+ )y的值是( )
A.5-3 B.3 C.3 -5 D.-3
二、填空题
9. 的平方根是±2
10.一个正数 的两个平方根分别是 与 ,则 的值是 .
11.计算:(﹣ )﹣3+ +2sin45°+( )0= .
12.比较3 2 ;
13.|x﹣5|+|2﹣x|的最小值为 .
14.我国数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根,华罗庚脱口说出答案39,邻座的乘客忙问计算的奥妙
(1)下面是探究 的过程,请补充完整:
①由103=1000,1003=1000000,可以确定 是两位数;
②由59319的个位上的数是9,可以确定 的个位上的数是9:
③如果划去59319后面的三位319得到数59,而33=27,44=64,可以确定 的十位上的数是 ;由此求得 =39
(2)已知103823也是一个整数的立方,请你用类似的方法求 =
15.计算:(-8)2019×0.1252018+(-3.14)0-( )-1的结果为 。
三、解答题
16.把下列各数分别填在相应的括号内:
,﹣3,0, ,0.3, ,﹣1.732, ,| |,﹣ ,﹣
整数{ };
分数{ };
无理数{ }.
已知 的平方根为±3,3a+2b-1的算术平方根为4,求a+2b的平方根.
已知三个互不相等的有理数,既可以表示为1,a,a+b的形式,又可以表示0, ,b的形式,试求a2n-1a2n(n≥1)的值.
已知 的立方根是3,16的算术平方根是 ,求: 的平方根.
20.课堂上老师讲解了比较 和 的方法,观察发现11-10=15-14=1,于是比较这两个数的倒数:
因为 ,所以 ,则有 ,
请你设计一种方法比较 与 的大小,
四、综合题
21.如图,已知实数 ,-1, ,4,其在数轴上所对应的点分别为点A,B,C,D.
(1)点B表示的数为 ,点D表示的数为 ;
(2)点C与点D之间的距离为 ;
(3)记点A与点B之间距离为a,点C与点D之间距离为b,求a+b的值.
22.阅读下面的文字,解答问题:大家知道 是无理数,而无理是无限不循环小数,因此 的小数部分我们不可能全部写出来,于是小明用 ﹣1来表示 的小数部分,事实上,小明的表示方法是有道理的,因为 的整数部分是1,将这个数减去其整数部分,差就是 的小数部分,又例如:∵23<( )2<32,即2< <3,∴ 的整数部分为2,小数部分为( ﹣2).
请解答
(1) 的整数部分是 ,小数部分是 .
(2)如果 的小数部分为a, 的整数部分为b,求a+b﹣ 的值.
(3)已知x是3+ 的整数部分,y是其小数部分,直接写出x﹣y的值.
23.
(1)用“<”“>”或“=”填空:1 , ;
(2)由以上可知:
①|1- |= ,②| - |=
(3)计算: (结果保留根号).
五、计算题
24.计算.
(1) ; (2) .
25.计算下列各式的值:
(1) ; (2) .
26.计算:
(1) (2) (3)
27.计算.
(1)﹣5﹣(﹣6)×. (2)4.8﹣(﹣1.2)+(﹣6)+|﹣4|.
(3). (4).
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】D
6.【答案】C
7.【答案】B
8.【答案】B
9.【答案】4
10.【答案】64
11.【答案】﹣2
12.【答案】>;>
13.【答案】3
14.【答案】(1)3
(2)47
15.【答案】-9
16.【答案】﹣3,0, , ;0.3, ,﹣1.732; , ,﹣ ,﹣
17.【答案】解:∵2b+1的平方根为±3,
∴2b+1=9,
解得:b=4,
∵3a+2b 1的算术平方根为4,
∴3a+2b 1=16,
则3a+8 1=16,
解得:a=3,
则a+2b=11,
故a+2b的平方根是:±
18.【答案】解:由题可得:a≠0,a+b=0,
∴ =-1,b=1,
∴a=-1,
又∵2n-1为奇数,-1的奇数次方得-1;2n为偶数,-1的偶数次方得1,
∴a2n-1 a2n=(-1)2n-1×(-1)2n=-1×1=-1.
19.【答案】解:∵ 的立方根是3,
∴ ,
∵16的算术平方根是 ,
∴ ,
∴ ,
解得: ,
∴ .
20.【答案】解:
21.【答案】(1);
(2)4
(3)解:由题意得,点A表示的数为-1,点C表示的数为4,点D表示的数为 ,
所以点A和点B之间距离为a= ,
点C和点D之间的距离为b= .
则a+b= .
22.【答案】(1)3;
(2)解:∵
∴,
∵ 的小数部分为a,
∴a=;
∵
∴,
∵ 的整数部分为b,
∴b=6;
∴ a+b﹣ =.
(3)解:
23.【答案】(1)<;<
(2) -1; -
(3)解:原式= = -1
24.【答案】(1)解:原式
(2)解:原式
25.【答案】(1)解:
(2)
.
26.【答案】(1)解:原式=-5-3
=-8;
(2)解:原式=×8-4×
=4-1
=3;
(3)解:原式=-1+8×+3
=-1+2+3
=4;
(4)解:原式=-9-6÷(-3)×4
=-9+2×4
=-9+8
=-1.
27.【答案】(1)解:原式
(2)解:原式
(3)解:原式
(4)解:原式
1 / 1
一、单选题
1.在实数 中, 无理数有( )个
A.1 B.2 C.3 D.4
2.在实数:,,,,,,中,无理数有( )
A.1个 B.2个 C.3个 D.4个
3.如图,在Rt△OBC中,OC=1,OB=2,数轴上点A所表示的数为a,则a的值是( )
A.- -2 B.-
C. ﹣2 D.﹣ +2
4.在实数|-3.14|,-3,- ,π中,最小的数是( )
A.- B.-3 C.|-3.14| D.π
5.在数轴上有三个互不重合的点A,B,C,它们代表的实数分别为a,b,c,下列结论中①若abc 0,则A,B,C三点中,至少有一个点在原点右侧;②若a+b+c=0,则A,B,C三点中,至少有一个点在原点右侧;③若a+c=2b,则点B为线段AC的中点;④O为坐标原点且A,B,C均不与O重合,若OB﹣OC=AB﹣AC,则bc 0,
所有正确结论的序号是( )
A.①② B.③④ C.①②③ D.①②③④
6.已知 , , 表示取三个数中最小的那个数﹒例如:当 , , , = , , =3﹒当 , , = 时,则 的值为( )
A. B. C. D.
7.数轴上A,B,C三点所代表的数分别是a、b、2,且 .下列四个选项中,有( )个能表示A,B,C三点在数轴上的位置关系.
①②③④
A.1个 B.2个 C.3个 D.4个
8.若6- 的整数部分为x,小数部分为y,则(2x+ )y的值是( )
A.5-3 B.3 C.3 -5 D.-3
二、填空题
9. 的平方根是±2
10.一个正数 的两个平方根分别是 与 ,则 的值是 .
11.计算:(﹣ )﹣3+ +2sin45°+( )0= .
12.比较3 2 ;
13.|x﹣5|+|2﹣x|的最小值为 .
14.我国数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根,华罗庚脱口说出答案39,邻座的乘客忙问计算的奥妙
(1)下面是探究 的过程,请补充完整:
①由103=1000,1003=1000000,可以确定 是两位数;
②由59319的个位上的数是9,可以确定 的个位上的数是9:
③如果划去59319后面的三位319得到数59,而33=27,44=64,可以确定 的十位上的数是 ;由此求得 =39
(2)已知103823也是一个整数的立方,请你用类似的方法求 =
15.计算:(-8)2019×0.1252018+(-3.14)0-( )-1的结果为 。
三、解答题
16.把下列各数分别填在相应的括号内:
,﹣3,0, ,0.3, ,﹣1.732, ,| |,﹣ ,﹣
整数{ };
分数{ };
无理数{ }.
已知 的平方根为±3,3a+2b-1的算术平方根为4,求a+2b的平方根.
已知三个互不相等的有理数,既可以表示为1,a,a+b的形式,又可以表示0, ,b的形式,试求a2n-1a2n(n≥1)的值.
已知 的立方根是3,16的算术平方根是 ,求: 的平方根.
20.课堂上老师讲解了比较 和 的方法,观察发现11-10=15-14=1,于是比较这两个数的倒数:
因为 ,所以 ,则有 ,
请你设计一种方法比较 与 的大小,
四、综合题
21.如图,已知实数 ,-1, ,4,其在数轴上所对应的点分别为点A,B,C,D.
(1)点B表示的数为 ,点D表示的数为 ;
(2)点C与点D之间的距离为 ;
(3)记点A与点B之间距离为a,点C与点D之间距离为b,求a+b的值.
22.阅读下面的文字,解答问题:大家知道 是无理数,而无理是无限不循环小数,因此 的小数部分我们不可能全部写出来,于是小明用 ﹣1来表示 的小数部分,事实上,小明的表示方法是有道理的,因为 的整数部分是1,将这个数减去其整数部分,差就是 的小数部分,又例如:∵23<( )2<32,即2< <3,∴ 的整数部分为2,小数部分为( ﹣2).
请解答
(1) 的整数部分是 ,小数部分是 .
(2)如果 的小数部分为a, 的整数部分为b,求a+b﹣ 的值.
(3)已知x是3+ 的整数部分,y是其小数部分,直接写出x﹣y的值.
23.
(1)用“<”“>”或“=”填空:1 , ;
(2)由以上可知:
①|1- |= ,②| - |=
(3)计算: (结果保留根号).
五、计算题
24.计算.
(1) ; (2) .
25.计算下列各式的值:
(1) ; (2) .
26.计算:
(1) (2) (3)
27.计算.
(1)﹣5﹣(﹣6)×. (2)4.8﹣(﹣1.2)+(﹣6)+|﹣4|.
(3). (4).
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】D
6.【答案】C
7.【答案】B
8.【答案】B
9.【答案】4
10.【答案】64
11.【答案】﹣2
12.【答案】>;>
13.【答案】3
14.【答案】(1)3
(2)47
15.【答案】-9
16.【答案】﹣3,0, , ;0.3, ,﹣1.732; , ,﹣ ,﹣
17.【答案】解:∵2b+1的平方根为±3,
∴2b+1=9,
解得:b=4,
∵3a+2b 1的算术平方根为4,
∴3a+2b 1=16,
则3a+8 1=16,
解得:a=3,
则a+2b=11,
故a+2b的平方根是:±
18.【答案】解:由题可得:a≠0,a+b=0,
∴ =-1,b=1,
∴a=-1,
又∵2n-1为奇数,-1的奇数次方得-1;2n为偶数,-1的偶数次方得1,
∴a2n-1 a2n=(-1)2n-1×(-1)2n=-1×1=-1.
19.【答案】解:∵ 的立方根是3,
∴ ,
∵16的算术平方根是 ,
∴ ,
∴ ,
解得: ,
∴ .
20.【答案】解:
21.【答案】(1);
(2)4
(3)解:由题意得,点A表示的数为-1,点C表示的数为4,点D表示的数为 ,
所以点A和点B之间距离为a= ,
点C和点D之间的距离为b= .
则a+b= .
22.【答案】(1)3;
(2)解:∵
∴,
∵ 的小数部分为a,
∴a=;
∵
∴,
∵ 的整数部分为b,
∴b=6;
∴ a+b﹣ =.
(3)解:
23.【答案】(1)<;<
(2) -1; -
(3)解:原式= = -1
24.【答案】(1)解:原式
(2)解:原式
25.【答案】(1)解:
(2)
.
26.【答案】(1)解:原式=-5-3
=-8;
(2)解:原式=×8-4×
=4-1
=3;
(3)解:原式=-1+8×+3
=-1+2+3
=4;
(4)解:原式=-9-6÷(-3)×4
=-9+2×4
=-9+8
=-1.
27.【答案】(1)解:原式
(2)解:原式
(3)解:原式
(4)解:原式
1 / 1
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
