反比例函数教案

九上第1章
目录
反比例函数
§1.1 反比例函数的概念、图象及性质.................2
§1.2 反比例函数的应用.............................10
§1.3 反思与总结...................................20
九上第1章 反比例函数
章节概述：反比例函数主要包括反比例函数的概念、图象、性质及应用，其中图象与性质及应用是中考数学中的重难点，经常和一次函数、二次函数及几何知识结合，考察学生的综合运用能力。在本章节中，老师将带领学生一起系统的梳理反比例函数的相关内容，使学生能较清晰地掌握反比例函数的图象和性质，进而提高分析和解决反比例函数主要题型的能力，并体会函数思想在生活中的应用。
§1.1 反比例函数的概念、图象及性质
§1.1.1 反比例函数的概念
知识目标：1、知道反比例函数的三种形式
2、确定反比例函数的比例系数及自变量取值范围
3、待定系数法确定反比例函数解析式
例1：下列函数中是反比例关系的有___________________（填序号）。
① ② ③ ④ ⑤
⑥ ⑦ ⑧ ⑨ ⑩为常数，
解析：反比例函数有三种形式：1、 2、k=xy 3、y=kx-1 (k0) 对照每小题，属于哪种类型，最好都转化成一般形式，并可以叫学生说出每个反比例函数的比例系数分别是多少。
答案：③⑤⑥⑩
即时练习：当n取什么值时，是反比例函数？
例2：若 是y关于x的反比例函数，则a的取值范围是 ；当a=3
时，比例系数是 ，自变量的取值是 。
解析：反比例函数的自变量x不能为0，k不能为0，y也不能为0。所以a-1≠0，a≠1。
当a=3可以把反比例函数看成，所以反比例系数是，自变量x的取值范围是x≠0的全体实数。
即时练习：
1、若函数是反比例函数，则m必须满足（ ）
A、m≠2；B、m≠0或m≠-2；C、m≠0；D、m≠0且m≠-2
2、面巾纸已成为很多人生活中必不可少的一种卫生清洁用品， 一刀200抽的面巾纸，若小丽家 x天用完，平均每天用y张.求y关于x的函数解析式，并求比例系数和自变量x的取值范围.
例题3：已知，而与成反比例，与成正比例，并且时，；时，，求y与x的函数关系式；
解析：本题考查待定系数法求解函数解析式，所以需要设待定系数，由于有两个函数，故比例系数要分别用k1和k2来表示。
与成反比例，与成正比例
，
把，及，代入
得
即时练习：
已知y=y1+y2．若y1与x2成正比例关系，y2与成反比例关系，且当x=-1时，y=3；当x=1时，y=-3．求y与x的函数关系式？
§1.1.2 反比例函数的图象
知识目标：1、在平面坐标系中画反比例函数图象
2、比例系数k决定反比例函数所在象限
3、反比例函数的对称性应用
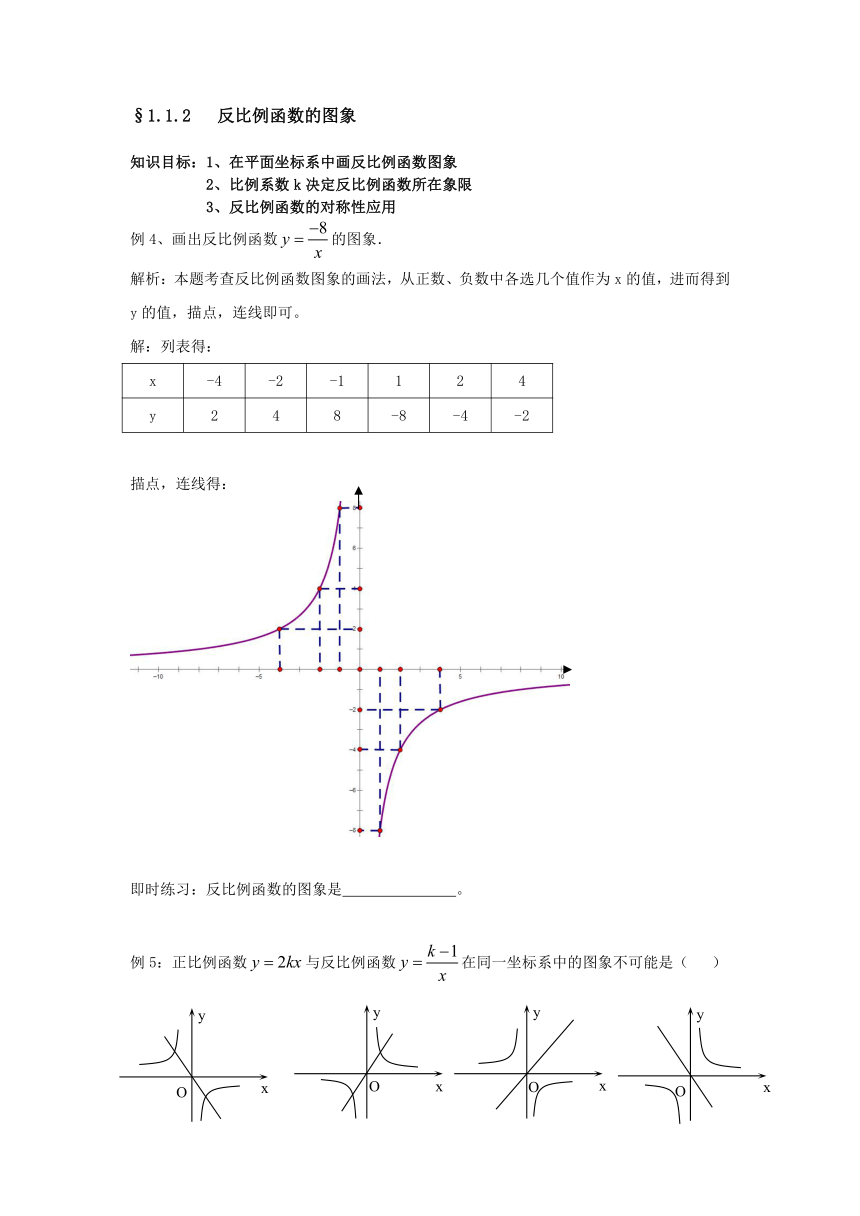
例4、画出反比例函数的图象．
解析：本题考查反比例函数图象的画法，从正数、负数中各选几个值作为x的值，进而得到y的值，描点，连线即可。
解：列表得：
x -4 -2 -1 1 2 4
y 2 4 8 -8 -4 -2
描点，连线得：
即时练习：反比例函数的图象是 。
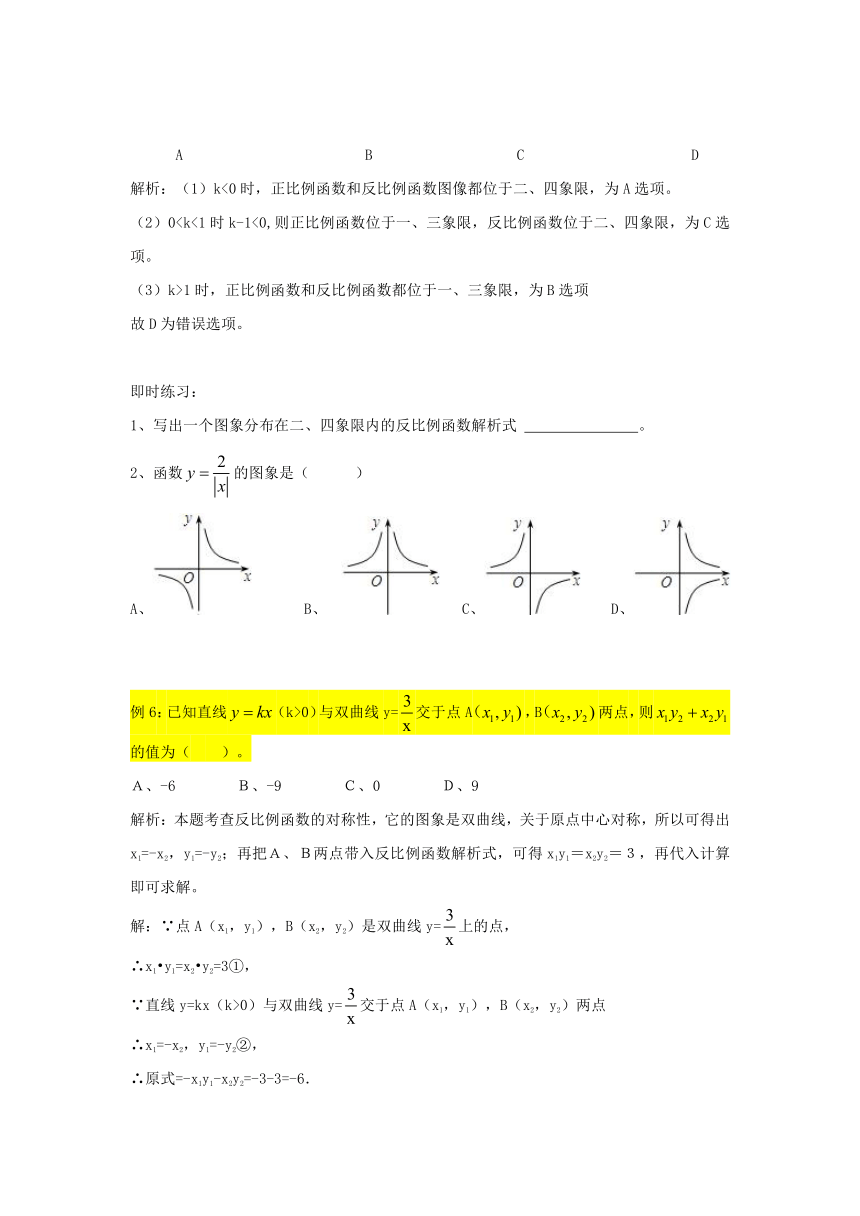
例5：正比例函数与反比例函数在同一坐标系中的图象不可能是（ 　）
A B C D
解析：（1）k<0时，正比例函数和反比例函数图像都位于二、四象限，为A选项。
（2）0（3）k>1时，正比例函数和反比例函数都位于一、三象限，为B选项
故D为错误选项。
即时练习：
1、写出一个图象分布在二、四象限内的反比例函数解析式 。
函数的图象是（ ）
A、 B、 C、 D、
例6：已知直线（k>0）与双曲线y=交于点A，B两点，则的值为（　　）。
Ａ、-6　　　　Ｂ、-9　　　　Ｃ、0　　　　Ｄ、9
解析：本题考查反比例函数的对称性，它的图象是双曲线，关于原点中心对称，所以可得出x1=-x2，y1=-y2；再把Ａ、Ｂ两点带入反比例函数解析式，可得x1y1＝x2y2＝３，再代入计算即可求解。
解：∵点A（x1，y1），B（x2，y2）是双曲线y=上的点，
∴x1 y1=x2 y2=3①，
∵直线y=kx（k>0）与双曲线y=交于点A（x1，y1），B（x2，y2）两点
∴x1=-x2，y1=-y2②，
∴原式=-x1y1-x2y2=-3-3=-6．
故选A．
总结：反比例函数的中心对称性常和正比例函数结合，考查交点问题，另外，反比例函数的图象还是轴对称图形，对称轴是直线y=x和y=-x。
即时练习：如图所示，点P（3a，a）是反比例函数y=（k＞0）与⊙O的一个交点，图中阴影部分的面积为10π，则反比例函数的解析式为（　　）
A、y= B、y= C、y= D、y=
§1.1.3 反比例函数的性质
知识目标：利用反比例函数的增减性比较函数值大小
例7：有下列函数：①y=-3x；②y=x-1；③；④。其中当x在各自的自变量取值范围内取值时，y随着x的增大而增大的函数有 。
解析：本题考查一次函数和反比例函数的增减性问题，一次函数中，当k>0时，y随着x的增大而增大；k<0时，y随着x的增大而减小。而反比例函数的增减性一定要在每个象限内，当时，在每个象限内，y随x的增大而减小；当时，在每个象限内，y随x的增大而增大。
解：①y=-3x，正比例函数，k＜0，故y随着x的增大而减小；
②y=x-1，一次函数，k＞0，故y随着x增大而增大；
③，反比例函数，k＜0，故在第二象限内y随x的增大而增大；
④，没有说在每个象限内，故不能说增减性。
注：反比例函数增减性必须强调在每个象限内，不能一概而论。
即时练习：
1、在反比例函数 (a为常数)的图象上有 A(-3,y1),B(-1,y2),C(2,y3)三点，比较函数值y1、y2、y3大小，并用“<”写出。
2、已知反比例函数的图象上有两点、且，那么下列结论正确的是（ ）
A. B. C. D.与之间的大小关系不能确定
同步突破：
A组
下列函数：①；②；③； ④； ⑤中，y是x的反比例函数的个数是（ ）
A、1 B、2 C、3 D、4
2、关于，下列说法正确的有（ ）个；
（1）一定是反比例函数；
（2）k为常数时，是反比例函数；
（3）当k≠0时，自变量x可为一切实数；
（4）当k≠0时，y的取值范围是一切实数。
A、0； B、1； C、2； D、3
3、如图，反比例函数y=图象的对称轴的条数是（　　）
A、0 B、1 C、2 D、3
4、若点（-2，y1), ( 1，y2), ( 2，y3）都在反比例函数的图象上，则有 （ ）
5、已知反比例函数，当时，其图象的两个分支在第二、四象限内；当时，其图象在每个象限内随的增大而减小。
6、已知y与3m成反比例，比例系数为k1，m又与6x成正比例，比例系数为k2，那么y与x成________函数，比例系数为_______．
7、反比例函数的图象过点（2，—2），求函数y与自变量x之间的关系式，它的图象在第几象限内？y随x的减小如何变化？试判断点（—3，0），（—3，—3）是否在此函数图象上？
8、如图，点A、B在反比例函数y=的图象上，且点A、B的横坐标分别为a，2a（a>0），AC垂直x轴于c，且△AOC的面积为2．
（1）求该反比例函数的解析式．
（2）若点（-a，y1），（-2a，y2）在该反比例函数的图象上，试比较y1与y2的大小．
B组
1、若是反比例函数，则是 函数；
2、如图,直线与双曲线交于两点,则的值为( )
http://www.21cnjy.com/ ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
A.-5 B.-10 C.5 D.10
3、如右图是三个反比例函数，，在x轴上方的图象，由此观察得到、、的大小关系为（ ）
A. B.
C. D.
4、若点A(m，－2)在反比例函数的图像上，则当函数值y≥－2时，自变量x的取值范围是___________.
5、设函数与的图象的交点坐标为（a，b），则的值为__________．
6、如图，函数的图象与函数（）的图象交于A、B两点，与轴交于C点，已知A点坐标为（2，1），C点坐标为（0，3）．
（1）求函数的表达式和B点的坐标；
（2）观察图象，比较当时，与的大小.
§1.2 反比例函数的应用
知识目标：1、用反比例函数解决实际问题 2、用反比例函数的几何意义求图形面积
3、反比例函数与一次函数综合 4、反比例函数与几何图形的数形结合
例8、某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P ( kPa ) 是气体体积V ( m3 ) 的反比例函数，其图象如图所示．当气球内的气压大于120 kPa时，气球将爆炸．为了安全起见，气球的体积应（ ）．
A．不小于m3 B．小于m3 C．不小于m3 D．小于m3
解析：本题考查反比例函数的应用，根据题意可知温度不变时，气球内气体的气压P（kPa）是气体体积V（m3）的反比例函数，且过点（1.6，60）故P V=96；故当P≤120，可判断V≥
解答：设球内气体的气压P（kPa）和气体体积V（m3）的关系式为P=
∵图象过点（1.6，60）
∴k=96
即P=在第一象限内，P随V的增大而减小，
∴当P≤120时，V=≥
故选C．
即时练习：
如图所示是某一蓄水池每小时的排水量V（m3/h）与排完水池中的水所用的时间t(h)之间的函数关系图象。
（1）请你根据图象提供的信息求出此蓄水池的蓄水量。
（2）写出此函数的解析式
（3）若要6h排完水池中的水，那么每小时的排水量应该是多少？
（4）如果每小时排水量是5m3，那么水池中的水将要多长时间排完？
例9、双曲线在第一象限内的图象如图所示，作一条平行于y轴的直线分别交双曲线于A、B两点，连接OA、OB，则△AOB的面积为（ ）
A．1 B．2
C．3 D．4
分析：本题考查反比例函数k的几何意义，如果设直线AB与x轴交于点C，那么△AOB的面积=△AOC的面积-△COB的面积．根据反比例函数的比例系数k的几何意义，知△AOC的面积=5，△COB的面积=3，从而求出结果．
解：设直线AB与x轴交于点C．
∵AB∥y轴，
∴AC⊥x轴，BC⊥x轴．
∵点A在双曲线y=的图象上，∴△AOC的面积=×10=5．
点B在双曲线y=的图象上，∴△COB的面积=×6=3
∴△AOB的面积=△AOC的面积-△COB的面积=5-3=2．
故选B．
例10、如图，已知双曲线(x＞0)经过矩形OABC的边AB中点F，交BC边于点E，
且四边形OEBF的面积为2，则k=　 　
解析：本题同样考查反比例函数的几何意义，但结合了几何图形。如果设F（x，y），表示点B坐标，再根据四边形OEBF的面积为2，列出方程，从而求出k的值
解：设F（x，y），那么B（x，2y），
∵E在反比例函数解析式上，
∴S△COE=k，
∵S四边形OEBF=S矩形ABCO-S△COE-S△AOF，且S四边形OEBF=2，
∴2xy-k-xy=2,
2k-k-k=2,
∴k=2．故本题答案为2．
注：本题的难点是根据点F的坐标得到其他点的坐标．在反比例函数上的点的横纵坐标的积等于反比例函数的比例系数。
即时练习：1、如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数的图象上。若点A的坐标为（－2，－2），则k的值为
A．1 B．－3 C．4 D．1或－3
2、如图，在中，点是直线与双曲线在第一象限的交点，且，则的值是_____.
例11、如图，已知反比例函数的图象与一次函数的图象交于两点A（-2，1）、B（a，-2）．
求反比例函数和一次函数的解析式；
若一次函数的图象交y轴于点C，求△AOC的面积（O为坐标原点）；
求使y1＞y2时x的取值范围．
解析：本题考点是反比例函数与一次函数的交点问题，用到的方法有数形结合、待定系数法等。
解：（1）∵函数y1=的图象过点A（-2，1），即1=；
∴m=-2，即y1=-，
又∵点B（a，-2）在y1=-上，
∴a=1，∴B（1，-2）．
又∵一次函数y2=kx+b过A、B两点，
即．
解之得．
∴y2=-x-1．
（2）∵x=0，∴y2=-x-1=-1，
即y2=-x-1与y轴交点C（0，-1）．
设点A的横坐标为xA，
∴△AOC的面积S△OAC=|OC|×|xA|=×1×2=1．
（3）要使y1＞y2，即函数y1的图象总在函数y2的图象上方．
∴-2＜x＜0，或x＞1．
即时练习：
如图，已知A（4，a），B（-2，-4）是一次函数y=kx+b的图象和反比例函数y= 的图象的交点．
（1）求反比例函数和一次函数的解祈式；
（2）求△A0B的面积．
例12、在反比例函数y=（x＞0）的图象上，有一系列点A1、A2、A3、…、An、An+1，若A1的横坐标为2，且以后每点的横坐标与它前一个点的横坐标的差都为2．现分别过点A1、A2、A3、…、An、An+1作x轴与y轴的垂线段，构成若干个矩形如图所示，将图中阴影部分的面积从左到右依次记为S1，S2，S3，…，Sn，则S1= ，S1+S2+S3+…+Sn= ．（用n的代数式表示）．
解析：由已知条件横坐标成等差数列，再根据点A1、A2、A3、…、An、An+1在反比例函数上，求出各点坐标，再由面积公式求出Sn的表达式，把n=1代入求得S1的值．
解：∵点A1、A2、A3、…、An、An+1在反比例函数y=（x＞0）的图象上，且每点的横坐标与它前一个点的横坐标的差都为2，又点A1的横坐标为2，∴A1（2，5），A2（4，）∴S1=2×（5﹣）=5；由题图象知，An（2n，），An+1（2n+2，），∴S2=2×（）=，∴图中阴影部分的面积知：Sn=2×（）=，（n=1，2，3，…）∵=，∴S1+S2+S3+…+Sn=10（++…+）=10（1）=．故答案为：．
点评： 此题是一道规律题，首先根据反比例函数的性质及图象，求出An的坐标的表达式，再由此求出Sn的表达式．
　即时练习：
如图，△P1OA1，△P2A1A2，△P3A2A3，…，是等腰直角三角形，点P1，P2，P3，…，在反比列函数y=的图象上，斜边OA1，A1A2，A2A3，…都在x轴上，则点A2的坐标是　　，An的坐标是　　　　.
同步突破
A组
1、如图（1）,A、C分别是反比例函数y＝图象上两点。若Rt△AOB
与Rt△COD的面积分别为S1,S2,则S1与S2的大小关系是( )
A.S1>S2 B.S1=S2； C.S12、面积为2的△ABC，一边长为x，这边上的高为y，则y与x的变化规律用图象表示大致是（ ）
3、如图，已知双曲线经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．若点A的坐标为（，4），则△AOC的面积为
A．12 B．9 C．6 D．4
4、某学校对教室采用药薰消毒法进行消毒．已知药物燃烧时，室内每立方米空气中的含药量y（毫克）与时间x（分钟）成正比例，药物燃烧后，y与x成反比例（如图所示），现测得药物8min燃毕，此时室内空气中每立方米的含药量为6mg，请你根据题中所提供的信息，解答下列问题．
（1）药物燃烧时y关于x的函数关系式为________，自变量x的取值范围是______；药物燃烧后y与x的函数关系式为__________．
（2）研究表明，当空气中每立方米的含药量低于1.6mg时学生方可进教室，那么从消毒开始，至少多少分钟后学生才能回到教室？
（3）研究表明，当空气中每立方米的含药量不低于3mg且持续时间不低于10min时，才能有效杀灭空气中的病菌，那么此次消毒是否有效？为什么？
5、如图，正方形OABC和正方形AEDF各有一个顶点在一反比例函数图象上，且正方形OABC的边长为2．
（1）求反比例函数的解析式；
（2）求点D的坐标．
6、已知反比例函数y＝(m为常数)的图象经过点A（－1，6）．
（1）求m的值；
（2）如图9，过点A作直线AC与函数y＝的图象交于点B，与x轴交于点C，且AB＝2BC，求点C的坐标．
7、如图，A是反比例函数图象上的一点，过A 作x轴的垂线，垂足为点B，当点A在其图象上移动时，△ABO的面积将会发生怎样的变化？对于其他反比例函数，是否也具有相同的现象？
8、如图，正比例函数的图象与反比例函数在第一象限的图象交于点，过点作轴的垂线，垂足为，已知的面积为1.
（1）求反比例函数的解析式；
（2）如果为反比例函数在第一象限图象上的点（点与点不重合），且点的横坐标为1，在轴上求一点，使最小.
B组
1、函数的图象与直线没有交点，那么k的取值范围是（ ）
A． B． C． D．
2、如图，已知在直角梯形AOBC中，AC∥OB，CB⊥OB，OB＝18，BC＝12，AC＝9，对角线OC、AB交于点D，点E、F、G分别是CD、BD、BC的中点，以O为原点，直线OB为x轴建立平面直角坐标系，则G、E、D、F四个点中与点A在同一反比例函数图像上的是（ ）
点G B．点E
C．点D D．点F．
3、两个反比例函数y=，y=在第一象限内的图象如图所示，点P1，P2，P3，…，P2005在反比例函数y=图象上，它们的横坐标分别是x1，x2，x3，…，x2005，纵坐标分别是1，3，5，…，共2005个连续奇数，过点P1，P2，P3，…，P2005分别作y轴的平行线，与y=的图象交点依次是Q1（x1，y1），Q2（x2，y2），Q3（x3，y3），…，Q2005（x2005，y2005），则y2005= ．
4、如图，在直角坐标系中，O为坐标原点. 已知反比例函数（k>0）的图象经过点A(2，m)，过点A作AB⊥x轴于点B，且△AOB的面积为 .
（1）求k和m的值；
（2）点C（x，y）在反比例函数的图象上，求当1≤x≤3时函数值y的取值范围；
（3）过原点O的直线l与反比例函数的图象交于P、Q两点，试根据图象直接写出线段PQ长度的最小值.
★★★5、已知点P的坐标为（m，0），在x轴上存在点Q（不与P点重合），以PQ为边作正方形PQMN，使点M落在反比例函数y = 的图像上.小明对上述问题进行了探究，发现不论m取何值，符合上述条件的正方形只有两个，且一个正方形的顶点M在第四象限，另一个正方形的顶点M1在第二象限.
（1）如图所示，若反比例函数解析式为y= ，P点坐标为（1，
0），图中已画出一符合条件的一个正方形PQMN，请你在图中画出符合条件的另一个正方形PQ1M1N1，并写出点M1的坐标； M1的坐标是
（2） 请你通过改变P点坐标，对直线M1 M的解析式y﹦kx＋b进行探究可得 k﹦ ， 若点P的坐标为（m，0）时，则b﹦ ；
（3） 依据(2)的规律，如果点P的坐标为（6，0），请你求出点M1和点M的坐标．
6、(1) 在图1中，已知线段AB，CD，其中点分别为E，F．
①若A (-1，0)， B (3，0)，则E点坐标为__________；
②若C (-2，2)， D (-2，-1)，则F点坐标为__________；
(2)在图1中，已知线段AB的端点坐标为A(a，b) ，B(c，d)，
求出图中AB中点D的坐标（用含a，b，c，d的
代数式表示），并给出求解过程．
●归纳 如图1中无论线段AB处于直角坐标系中的哪个位置，
当其端点坐标为A(a，b)，B(c，d)， AB中点为D(x，y) 时，
x=_________，y=___________．（不必证明）
●运用 在图2中，一次函数与反比例函数
的图象交点为A，B．
①求出交点A，B的坐标；
②若以A，O，B，P为顶点的四边形是平行四边形，
请利用上面的结论求出顶点P的坐标．
§1.3 反思与总结
知识点l. 反比例函数的概念
重点：掌握反比例函数的概念
难点：理解反比例函数的概念
一般地，如果两个变量x、y之间的关系可以表示成或y=kx-1或k=xy（k为常数，）的形式，那么称y是x的反比例函数。
反比例函数的概念需注意以下几点：
（1）k是常数，且k不为零；
（2）中分母x的指数为1，如，就不是反比例函数。
（3）自变量x的取值范围是的一切实数.
（4）自变量y的取值范围是的一切实数。
知识点2. 反比例函数的图象及性质
重点：掌握反比例函数的图象及性质
难点：反比例函数的图象及性质的运用
反比例函数的图象是双曲线，它有两个分支，这两个分支分别位于第一、三象限或第二、四象限。它们关于原点对称、反比例函数的图象与x轴、y轴都没有交点，即双曲线的两个分支无限接近坐标轴，但永远不与坐标轴相交。
画反比例函数的图象时要注意的问题：
（1）画反比例函数图象的方法是描点法；
（2）画反比例函数图象要注意自变量的取值范围是，因此不能把两个分支连接起来。
（3）由于在反比例函数中，x和y的值都不能为0，所以画出的双曲线的两个分支要分别体现出无限的接近坐标轴，但永远不能达到x轴和y轴的变化趋势。
反比例函数的性质:
的变形形式为（常数）所以：
（1）其图象的位置是：
当时，x、y同号，图象在第一、三象限；
当时，x、y异号，图象在第二、四象限。
（2）若点(m,n)在反比例函数的图象上，则点（-m,-n）也在此图象上，故反比例函数的图象关于原点对称。
（3）当时，在每个象限内，y随x的增大而减小；
当时，在每个象限内，y随x的增大而增大；
知识点3. 反比例函数解析式的确定。
重点：掌握反比例函数解析式的确定
难点：由条件来确定反比例函数解析式
（1）反比例函数关系式的确定方法：待定系数法，由于在反比例函数关系式中，只有一个待定系数k，确定了k的值，也就确定了反比例函数，因此只需给出一组x、y的对应值或图象上点的坐标，代入中即可求出k的值，从而确定反比例函数的关系式。
（2）用待定系数法求反比例函数关系式的一般步骤是：
①设所求的反比例函数为：（）；
②根据已知条件，列出含k的方程；
③解出待定系数k的值；
④把k值代入函数关系式中。
知识点4. 用反比例函数解决实际问题
反比例函数的应用须注意以下几点：
①反比例函数在现实世界中普遍存在，在应用反比例函数知识解决实际问题时，要注意将实际问题转化为数学问题。
②针对一系列相关数据探究函数自变量与因变量近似满足的函数关系。
③列出函数关系式后，要注意自变量的取值范围。
反比例函数单元测试卷
一、选择题（本大题共10小题，每小题3分，共30分）
1．反比例函数的图象在（　 　）
A．第一、三象限 B．第二、四象限 C．第一、二象限 D．第三、四象限
2．若反比例函数的图象经过点（－3，2），则的值为 （ ）．
A．-5 B．5 C．－6 D．6
3．如图，反比例函数的图象与直线的交点为A，B，过点A作y轴的平行线与过点B作x轴的平行线相交于点C，则的面积为（　　）
A．2 B．4 C．6 D．8
4.反比例函数y＝的图象，当x＞0时，y随x的增大
而增大，则k的取值范围是（ ）．
（A）k＜3 （B）k≤3 （C）k＞3 （D）k≥3
★5.如图，若点M是x轴正半轴上任意一点，过点M作PQ∥y轴，分别交函数和的图象于点P和Q，连接OP和OQ．则下列结论正确的是（　　）
A．∠POQ不可能等于90°　　 B．　　
C．这两个函数的图象一定关于x轴对称　　D．△POQ的面积是
6.已知一个矩形的面积为24cm2，其长为ycm，宽为xcm，则y与x之间的函数关系的图象大致是（ ）
A B C D
7.函数与函数在同一坐标系中的大致图像是（ ）
8．下列函数：①；②；③；④．当时，y随x的增大而减小的函数有（ ）
A．1 个 B．2 个 C．3 个 D．4 个
9．已知是反比例函数的图象上的三点，且，则的大小关系是（　 　）
Ａ． Ｂ． Ｃ． Ｄ．
10.如图，函数和函数的图象相交于点M(2，m)，N(-1，n)，若，则x的取值范围是（ ）
A． B．
C． D．
二、填空题（每小题4分，共24分）
11.已知反比例函数的图象经过（1，－2）．则 ．
12．写出一个图象分布在二、四象限内的反比例函数解析式 .
13某种灯的使用寿命为1000小时，它的可使用天数y与平均每天使用的小时数x之间的关系式为 .
14．如图, 如果函数y=－x与y=的图像交于A、B两点, 过点A作AC垂直于y轴, 垂足为点C, 则△BOC的面积为_________.
★★★15.如图，已知函数y=2x和函数的图象交于A、B两点，过点A作AE⊥x轴于点E，若△AOE的面积为4，P是坐标平面上的点，且以点B、O、E、P为顶点的四边形是平行四边形，则满足条件的P点坐标是　_________　．
　
16.如图，若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=(x＞0)的图象上，则点E的坐标是（ ， ）.
三、解答题（共66分）
17．已知，而与成反比例，与成正比例，并且时，；时，，求y与x的函数关系式；
18．如图，已知双曲线y=经过点D（6，1），点C是双曲线第三象限上的动点，过C作CA⊥x轴，过D作DB⊥y轴，垂足分别为A，B，连接AB，BC
（1）求k的值；
（2）若△BCD的面积为12，求直线CD的解析式；
（3）判断AB与CD的位置关系，并说明理由．
19．如图，点A、B在反比例函数y=的图象上，且点A、B的横坐标分别为a，2a（a>0），AC垂直x轴于c，且△AOC的面积为2．
（1）求该反比例函数的解析式．
（2）若点（-a，y1），（-2a，y2）在该反比例函数的图象上，试比较y1与y2的大小．
20．为了预防流感，某学校在休息天用药熏消毒法对教室进行消毒．已知药物释放过程中，室内每立方米空气中的含药量（毫克）与时间（分钟）成正比例；药物释放完毕后，与成反比例，如图9所示．根据图中提供的信息，解答下列问题：
（1）、写出从药物释放开始，与之间的两个函数关系式及相应的自变量取值范围；
（2）、据测定，当空气中每立方米的含药量降低到0.45毫克以下时，学生方可进入教室，那么从药物释放开始，至少需要经过多少小时后，学生才能进入教室？
21.某蓄水池的排水管每小时排水8m3,6小时可将满池水全部排空.
(1)蓄水池的容积是多少
(2)如果增加排水管,使每小时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化
(3)写出t与Q之间的关系式.
(4)如果准备在5h内将满池水排空,那么每小时的排水量至少为多少
(5)已知排水管的最大排水量为每小时12m3,那么最少多长时间可将满池水全部排空
22．如图，函数的图象与函数（）的图象交于A、B两点，与轴交于C点，已知A点坐标为（2，1），C点坐标为（0，3）．
（1）求函数的表达式和B点的坐标；
（2）观察图象，比较当时，与的大小.
23．如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A，C分别在坐标轴上，顶点B的坐标为（4，2）．过点D（0，3）和E（6，0）的直线分别与AB，BC交于点M，N．
（1）求直线DE的解析式和点M的坐标；
（2）若反比例函数（x＞0）的图象经过点M，求该反比例函数的解析式，并通过计算判断点N是否在该函数的图象上；
（3）若反比例函数（x＞0）的图象与△MNB有公共点，请直接写出m的取值范围．
答案：
1—5：A C D A D
6—10：D B B C D
11、-2
12、y=-1/x
13、y=1000/x
14、2
15、P1（0，-4）P2（-4，-4）P3（4，4）
16、（根号5+1）/2，（根号5-1）/2
17、与成反比例，与成正比例
，
把，及，代入
得
18、
解答： 解：（1）∵双曲线y=经过点D（6，1），∴=1，解得k=6；（2）设点C到BD的距离为h，∵点D的坐标为（6，1），DB⊥y轴，∴BD=6，∴S△BCD=×6 h=12，解得h=4，∵点C是双曲线第三象限上的动点，点D的纵坐标为1，∴点C的纵坐标为1﹣4=﹣3，∴=﹣3，解得x=﹣2，∴点C的坐标为（﹣2，﹣3），设直线CD的解析式为y=kx+b，则，解得，所以，直线CD的解析式为y=x﹣2；（3）AB∥CD．理由如下：∵CA⊥x轴，DB⊥y轴，设点C的坐标为（c，），点D的坐标为（6，1），∴点A、B的坐标分别为A（c，0），B（0，1），设直线AB的解析式为y=mx+n，则，解得，所以，直线AB的解析式为y=﹣x+1，设直线CD的解析式为y=ex+f，则，解得，∴直线CD的解析式为y=﹣x+，∵AB、CD的解析式k都等于﹣相等，∴AB与CD的位置关系是AB∥CD．
19、∵S△AOC=2，
∴k=2S△AOC=4；
∴y=4/X
（2）∵k＞0，
∴函数y在各自象限内随x的增大而减小；
∵a＞0，
∴-2a＜-a；
∴y1＜y2；
20、（1）Y=108/X（x≥12）；
（2）解之得x=240（分钟）=4（小时），
答：从药物释放开始，至少需要经过4小时后，学生才能进入教室．
21、解：（1）蓄水池的容积是：8×6=48m3；
（2）∵Q×t=48，Q与t成反比例关系．
∴Q增大，t将减少；
（3）t与Q之间的关系式为t=48/Q
（4）∵t=48/Q≤5，解不等式得，Q≥9.6，即每小时的排水量至少为9.6m3；
（5）当Q=12时，由Q×t=48得t=4，即最少用4h可将满池水全部排空．
22、分析：
（1）把A（2，1），C（0，3）代入y1=k1x+b可求出k1和b；把A（2，1）代入y=K2/X
（x＞0）求出k2，然后把两个解析式联立起来解方程组即可求出B点坐标；
（2）观察函数图象，当x＞0，两图象被A，B分成三段，然后分段判断大小以及对应的x的值．
解：（1）由题意，得
y1=-x+3
点B的坐标为（1，2）；
（2）当0＜x＜1或x＞2时，y1＜y2；
当1＜x＜2时，y1＞y2；
当x=1或x=2时，y1=y2．
23、（1）设直线DE的解析式为:y=kx+b
∵点D ，E的坐标为（0，3）、（6，0），
∴ b= 3
6k+b=0
6k+3=0
6k=-3
k=-0.5
得 k=-0.5 b=3
∴y =-0.5x+3
∵ 点M在AB边上，B（4，2），而四边形OABC是矩形，
∴ 点M的纵坐标为2．
又 ∵ 点M在直线y=-0.5x+b上，
∴-0.5x+b =2
∵ b=3
∴ x = 2．
∴ M（2,2）．
（2）∵y=m/x（x＞0）经过点M（2，2），
∴ m=4
∴. y=4/x
又 ∵ 点N在BC边上，B（4，2），
∴点N的横坐标为4．
∵ 点N在直线y=-0.5x+b上，
∴ y=1
∴ N（4，1）．
∵ 当x=4时，y = 1，
∴点N在函数 的图象上．
（3）4≤ m ≤8
同步练习答案：
反比例函数
1、1节
A组
1—4：BACD
5、<2/3，>2/3
6、反比例，
k1
18xk2
7、y=-4/x; 二、四象限；Y随X的增大而增大；不在
8、∵S△AOC=2，
∴k=2S△AOC=4；
∴y=4/X
（2）∵k＞0，
∴函数y在各自象限内随x的增大而减小；
∵a＞0，
∴-2a＜-a；
∴y1＜y2；
B组
1、反比例 2、B 3、B 4、x≤-2或x＞0 5、-1/2
6、（1）把A（2，1），C（0，3）代入y1=k1x+b可求出k1和b；把A（2，1）代入y=K2/X
（x＞0）求出k2，然后把两个解析式联立起来解方程组即可求出B点坐标；
（2）观察函数图象，当x＞0，两图象被A，B分成三段，然后分段判断大小以及对应的x的值．
解：（1）由题意，得
y1=-x+3
点B的坐标为（1，2）；
（2）当0＜x＜1或x＞2时，y1＜y2；
当1＜x＜2时，y1＞y2；
当x=1或x=2时，y1=y2．
反比例函数1、2节
A组
1—3：B C B
4、（1）y= 3/4X；0≤x≤8；y= 48/X（x＞8）
（2）30
（3）3=3/4X得x=4，
3=48/X得x=16，
16-4=12＞10，
所以此次消毒有效
5、解：（1）∵正方形OABC和正方形AEDF各有一个顶点在一反比例函数图象上，且正方形OABC的边长为2．
∴B点坐标为：（2，2），
设反比例函数的解析式为y=K/X
∴xy=k=4，
∴反比例函数的解析式为y=4/X
（2）设正方形ADEF的边长为a，则D（2+a，a），
代入反比例函数y=4/X（x＞0）得：4=（2+a）a，又a＞0，
解得：a=-1+根号5
D（1+根号5，-1+根号5）
6、(1)m=2
(2) C（4，0　）
7、当A点在其图象上移动时，面积总是等于7
这个结论对所有的反比例函数都适用
8、1)S△OAM= |k|=1，k=±2，由两函数在第一象限相交，则k=2.
反比例函数为y=2/x
(2)把x=1代入y=2/x，得y=2，所以B(1,2)
B关于X轴的对称点是B′(1,-2)
求得直线AB′为y=3x-5,
y=3x-5与X轴交点（5/3，0）即为P。
B组：
1、A
2、A
3、2004.5
4、（1）∵A（2，m）∴OB=2 ∵s△AOB=1/2∴1/2*OB*AB=1/2∴AB=1/2即m=1/2
∴A（2，1/2）所以k=2*1/2=1
（2）∵k=1∴y=1/x
当x=1时y=1
当x=3时y=1/3
所以当1≤x≤3时1/3≤y≤1
（3）当x=y时即p（1，1）Q（-1，-1）时PQ最短长为2倍根号2，最后约等于2.83
5、（1）M1的坐标是 （-1，2）
（2）K=-1，b=m
(3)由（2）知，直线M1 M的解析式为: y=-x+6
则M(x，y)满足x(-x+6)=-2
解得 x1=3-根号11，x2=3+根号11
y1=3+根号11,y2=3－根号11
∴ M,的坐标为（3-根号11，3+根号11），) ,M（3+根号11，3－根号11）
6、
解：探究 ①根据A （-1，0），B （3，0），线段AB中点为E，
∴E点坐标为：（1，0）；
②根据C （-2，2），D （-2，-1），线段CD中点为F，
∴F点坐标为：（-2，1/2）
归纳：过点A，D，B三点分别作x轴的垂线，垂足分别为A'，D'，B'，
则AA'∥BB'∥DD'．
X= (a+c)/2 Y=(b+d)/2
A（-1，-3），B（3，1）．
②以AB为对角线时，由上面的结论知AB中点M的坐标为（1，-1）．
∵平行四边形对角线互相平分，
∴OM=MP，即M为OP的中点．
∴P点坐标为（2，-2）．（1分）
当OB为对角线时，PB=AO，PB∥AO，
同理可得：点P坐标分别为（4，4），
以OA为对角线时，PA=BO，PA∥BO，
可得：点P坐标分别为（-4，-4）．
∴满足条件的点P有三个，
坐标分别是（2，-2），（4，4），（-4，-4）．
x
O
y
x
O
y
x
O
y
x
O
y
第3题
第8题
A
B
O
C
x
y
x
y
O
A
B
C
D
第4题
(第8题)
B
O
A
y
P
Q
M
N
O
x
1
2
-1
-2
-3
-3
-2
-1
1
2
3
(第5题图)
O
x
y
D
B
图一
A
x
y
y=
y=x-2
A
B
O
图2
A
O
B
C
第3题
x
y
o
x
y
o
x
y
o
x
y
o
第16题
O
9
（毫克）
12
（分钟）
图9
A
B
O
C
x
y
x
M
N
y
D
A
B
C
E
O
第23题