3.2不等式的基本性质 课件(共21张PPT)
文档属性
| 名称 | 3.2不等式的基本性质 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 291.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 15:18:28 | ||
图片预览





文档简介
(共21张PPT)
5.2 不等式的基本性质
清楚地,对不等式的两端施加什么运算
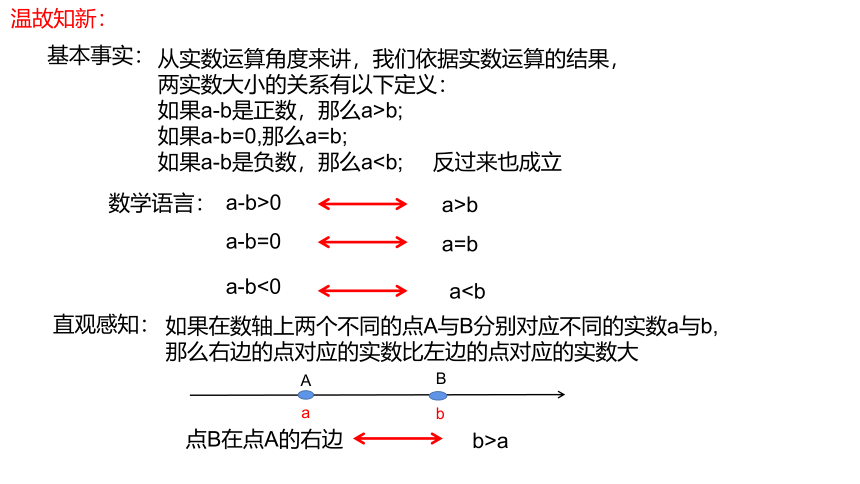
基本事实:
从实数运算角度来讲,我们依据实数运算的结果,
两实数大小的关系有以下定义:
如果a-b是正数,那么a>b;
如果a-b=0,那么a=b;
如果a-b是负数,那么a数学语言:
a-b>0
a>b
a-b=0
a=b
a-b<0
a温故知新:
直观感知:
如果在数轴上两个不同的点A与B分别对应不同的实数a与b,那么右边的点对应的实数比左边的点对应的实数大
A
a
B
b
点B在点A的右边
b>a
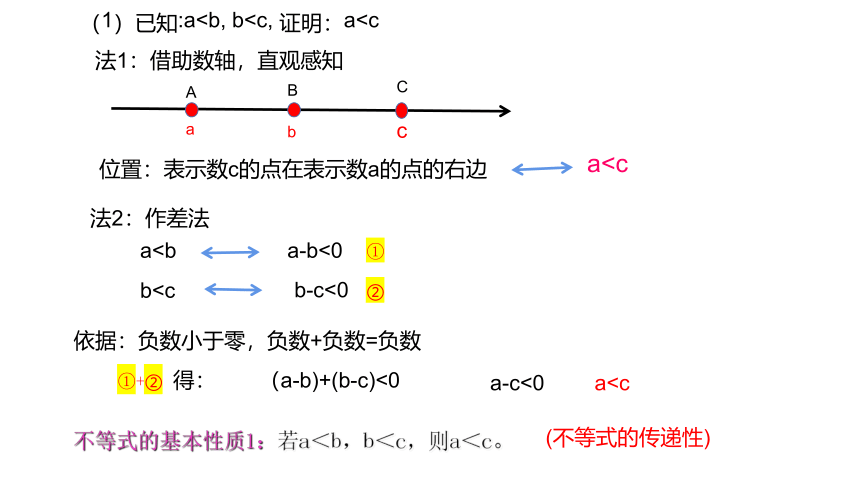
(1)已知:aa位置:表示数c的点在表示数a的点的右边
法1:借助数轴,直观感知
B
b
A
a
c
C
法2:作差法
aa-b<0 ①
bb-c<0 ②
依据:负数小于零,负数+负数=负数
①+② 得:
(a-b)+(b-c)<0
a-c<0
a不等式的基本性质1:若a<b,b<c,则a<c。
(不等式的传递性)
(2)比较大小
3___5; 3+2___5+2; 3-2___5-2
7___4 ; 7+(-2)___4+(-2); 7-(-2)___4-(- 2)
若a>b,那么a+c__b+c,a-c__b-c.
<
<
<
>
>
>
>
>
若a<b,那么a+c__b+c,a-c__b-c.
<
<
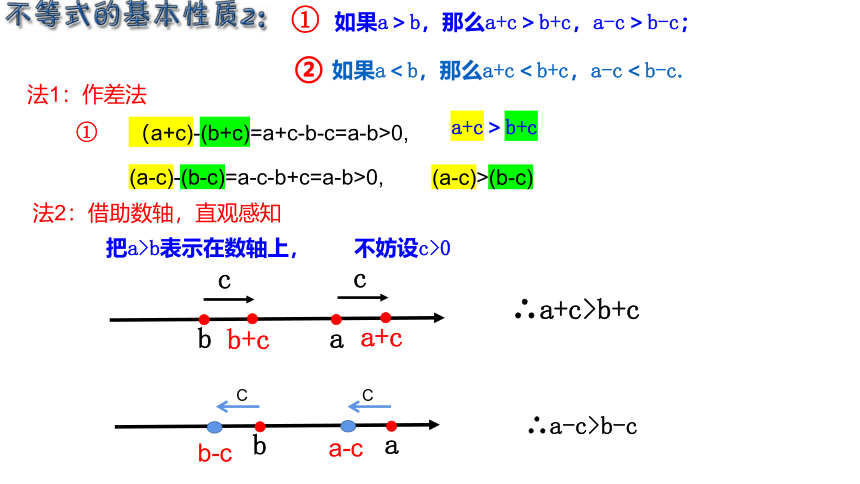
不等式的基本性质2:
不等式的两边都加上(或减去)同一个数,所得到的不等式仍成立.
(不等号方向不变)
① 如果a>b,那么a+c>b+c,a-c>b-c;
② 如果a<b,那么a+c<b+c,a-c<b-c.
法1:作差法
a+c>b+c
(a+c)-(b+c)=a+c-b-c=a-b>0,
①
(a-c)-(b-c)=a-c-b+c=a-b>0,
(a-c)>(b-c)
把a>b表示在数轴上,
不妨设c>0
法2:借助数轴,直观感知
b
a
b
a
b+c
c
a+c
c
∴a+c>b+c
C
b-c
C
a-c
∴a-c>b-c
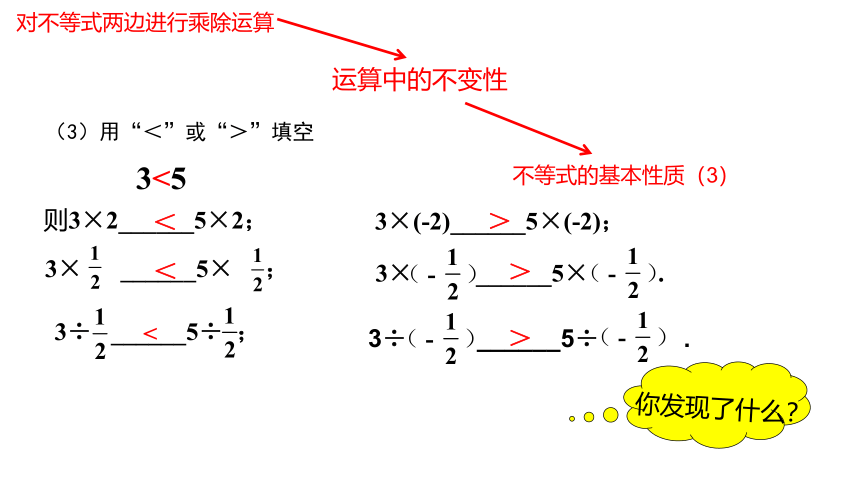
3<5
则3×2______5×2;
<
<
3× ______5× ;
3÷ ______5÷ ;
<
>
3÷ ______5÷ .
3×(-2)______5×(-2);
>
3× ______5× .
>
(3)用“<”或“>”填空
你发现了什么?
运算中的不变性
不等式的基本性质(3)
对不等式两边进行乘除运算
如果a>b,c>0,那么ac____bc(或 ).
>
不等式的基本性质3①:
不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
不等式的基本性质3②:
不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
用字母表示:
用字母表示:
在不等式的两边施加运算,发现的规律是运算后所保持的不等号方向不变或要求不等号方向必须改变
如果a>b,c<0,那么ac ___bc(或 ).
.
归纳:不等式的基本性质:
性质3:不等式的两边都乘(或都除以)同一个正数,所得到的不等式仍成立;
不等式的两边都乘(或都除以)同一个负数,必须把不等号的方向改变,所得到的不等式成立.
性质1:若a<b,b<c,则a<c。
性质2:不等式的两边都加上(或减去)同一个数,所得到的不等式仍成立.
(不等号方向不变)
(不等号方向不变)
(不等号方向改变)
(传递性)
例1.将下列不等式化成“x > a”或“x < a”的形式:
(1)x - 5 > -1. (2)-2x > 3.
解:(1)根据不等式的基本性质1,在不等式两边都加5,得x - 5 + 5 > -1 + 5,即x > 4.
典例解析
学以致用:
(2)根据不等式的基本性质3,在不等式两边都除以 -2,得 x < -
。
解:(1)不等式的两边都减去2x,由不等式基本性质2,
.变式:将下列不等式化成“x>a”或“x<a”的形式:
(1) 3x < 2x -3 (2)-x< (3) x<3
(3) 根据不等式的基本性质3,两边都乘以2,
得x≤6.
得 3x -2x < 2x-3-2x,
即 x < -3.
(2)根据不等式的基本性质3,两边都除以-1,
得x>-
解法二:(借助数轴)
例2 已知a<0 ,试比较2a与a的大小.
解法一:(不等式的基本性质3)
∵2>1,a<0,
∴2a<a.
如图,在数轴上分别表示2a和a的点(a<0).
2a位于a的左边,所以2a<a.
0
a
2a
∣a∣
∣a∣
解法三:(利用不等式基本性质2)
∵a<0,
∴ a+a<0+a,
即2a <a.
已知a<0 ,试比较2a与a的大小.
解法四: (作差法)
∵2a-a=a <0,
∴2a<a.
解法5:特殊值法:
设a=-1,则 2a=-2.
∵-2<-1,∴2a <a.
已知a<0 ,试比较2a与a的大小.
∵2a÷a=2>1, a<0,
∴ 2a作差与0比较,作商与1比较
解法6:作商与“1”比较法
比较2a与a的大小
(1)当a>0时,2a>a;
(2)当a=0时,2a=a;
(3)当a<0时,2a变式:
1.选择适当的不等号填空:
(1)∵0 __ 1,
∴ a___a+1(不等式的基本性质2);
(2)∵(a-1)2___ 0,
∴(a - 1)2 -2___-2( )
<
<
≥
≥
不等式的基本性质2
当堂检测:
夯实基础,稳扎稳打
<
<
>
<
>
2、已知 a﹤b,用“<”或“>”号填空:
(1) a-4____b-4; (2)3a____3b;
(3)-a-2____-b -2; (4)a-b____0;
(5)-—a____-—b;
(6)ac2_____bc2 ( c 为有理数 )
(7)a(c2+1) ____b(c2 +1) ( c 为有理数 )
1
3
1
3
≤
<
D
3.有一道这样的题:“由★x>1得到 x< ”,
则题中★表示的是( )
A.非正数 B.正数
C.非负数 D.负数
4.若 x 比较 2-3x 与2-3y 的大小,并说明理由。
解:∵x<y
∴-3x>-3y
(不等式性质3)
∴2-3x>2-3y
(不等式性质2)
连续递推,豁然开朗
5.小明和小华在探究数学问题.
小明说: “ 3y>4y ”.
小华认为小明说错了,应该是3y<4y,
聪明的你觉得呢
谁做对了
当y>0时, 3y < 4y;
当y= 0时, 3y = 4y;
当y < 0时, 3y >4y.
6.若 x ,且(a-3)x
解:∵x<y, (a-3)x>(a-3)y
∴a-3<0
(不等式性质3)
∴a<3
(不等式性质2)
7.如果 , 那么xy 0.
(依据 )
.
>
不等式的基本性质3
8.如果b<0,你能比较a-b,a+b的大小吗?
a-b>a+b
作差法比较大小:
(a-b)-(a+b)=a-b-a-b=-2b
.
5.2 不等式的基本性质
清楚地,对不等式的两端施加什么运算
基本事实:
从实数运算角度来讲,我们依据实数运算的结果,
两实数大小的关系有以下定义:
如果a-b是正数,那么a>b;
如果a-b=0,那么a=b;
如果a-b是负数,那么a
a-b>0
a>b
a-b=0
a=b
a-b<0
a
直观感知:
如果在数轴上两个不同的点A与B分别对应不同的实数a与b,那么右边的点对应的实数比左边的点对应的实数大
A
a
B
b
点B在点A的右边
b>a
(1)已知:a
法1:借助数轴,直观感知
B
b
A
a
c
C
法2:作差法
a
b
依据:负数小于零,负数+负数=负数
①+② 得:
(a-b)+(b-c)<0
a-c<0
a
(不等式的传递性)
(2)比较大小
3___5; 3+2___5+2; 3-2___5-2
7___4 ; 7+(-2)___4+(-2); 7-(-2)___4-(- 2)
若a>b,那么a+c__b+c,a-c__b-c.
<
<
<
>
>
>
>
>
若a<b,那么a+c__b+c,a-c__b-c.
<
<
不等式的基本性质2:
不等式的两边都加上(或减去)同一个数,所得到的不等式仍成立.
(不等号方向不变)
① 如果a>b,那么a+c>b+c,a-c>b-c;
② 如果a<b,那么a+c<b+c,a-c<b-c.
法1:作差法
a+c>b+c
(a+c)-(b+c)=a+c-b-c=a-b>0,
①
(a-c)-(b-c)=a-c-b+c=a-b>0,
(a-c)>(b-c)
把a>b表示在数轴上,
不妨设c>0
法2:借助数轴,直观感知
b
a
b
a
b+c
c
a+c
c
∴a+c>b+c
C
b-c
C
a-c
∴a-c>b-c
3<5
则3×2______5×2;
<
<
3× ______5× ;
3÷ ______5÷ ;
<
>
3÷ ______5÷ .
3×(-2)______5×(-2);
>
3× ______5× .
>
(3)用“<”或“>”填空
你发现了什么?
运算中的不变性
不等式的基本性质(3)
对不等式两边进行乘除运算
如果a>b,c>0,那么ac____bc(或 ).
>
不等式的基本性质3①:
不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
不等式的基本性质3②:
不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
用字母表示:
用字母表示:
在不等式的两边施加运算,发现的规律是运算后所保持的不等号方向不变或要求不等号方向必须改变
如果a>b,c<0,那么ac ___bc(或 ).
.
归纳:不等式的基本性质:
性质3:不等式的两边都乘(或都除以)同一个正数,所得到的不等式仍成立;
不等式的两边都乘(或都除以)同一个负数,必须把不等号的方向改变,所得到的不等式成立.
性质1:若a<b,b<c,则a<c。
性质2:不等式的两边都加上(或减去)同一个数,所得到的不等式仍成立.
(不等号方向不变)
(不等号方向不变)
(不等号方向改变)
(传递性)
例1.将下列不等式化成“x > a”或“x < a”的形式:
(1)x - 5 > -1. (2)-2x > 3.
解:(1)根据不等式的基本性质1,在不等式两边都加5,得x - 5 + 5 > -1 + 5,即x > 4.
典例解析
学以致用:
(2)根据不等式的基本性质3,在不等式两边都除以 -2,得 x < -
。
解:(1)不等式的两边都减去2x,由不等式基本性质2,
.变式:将下列不等式化成“x>a”或“x<a”的形式:
(1) 3x < 2x -3 (2)-x< (3) x<3
(3) 根据不等式的基本性质3,两边都乘以2,
得x≤6.
得 3x -2x < 2x-3-2x,
即 x < -3.
(2)根据不等式的基本性质3,两边都除以-1,
得x>-
解法二:(借助数轴)
例2 已知a<0 ,试比较2a与a的大小.
解法一:(不等式的基本性质3)
∵2>1,a<0,
∴2a<a.
如图,在数轴上分别表示2a和a的点(a<0).
2a位于a的左边,所以2a<a.
0
a
2a
∣a∣
∣a∣
解法三:(利用不等式基本性质2)
∵a<0,
∴ a+a<0+a,
即2a <a.
已知a<0 ,试比较2a与a的大小.
解法四: (作差法)
∵2a-a=a <0,
∴2a<a.
解法5:特殊值法:
设a=-1,则 2a=-2.
∵-2<-1,∴2a <a.
已知a<0 ,试比较2a与a的大小.
∵2a÷a=2>1, a<0,
∴ 2a
解法6:作商与“1”比较法
比较2a与a的大小
(1)当a>0时,2a>a;
(2)当a=0时,2a=a;
(3)当a<0时,2a
1.选择适当的不等号填空:
(1)∵0 __ 1,
∴ a___a+1(不等式的基本性质2);
(2)∵(a-1)2___ 0,
∴(a - 1)2 -2___-2( )
<
<
≥
≥
不等式的基本性质2
当堂检测:
夯实基础,稳扎稳打
<
<
>
<
>
2、已知 a﹤b,用“<”或“>”号填空:
(1) a-4____b-4; (2)3a____3b;
(3)-a-2____-b -2; (4)a-b____0;
(5)-—a____-—b;
(6)ac2_____bc2 ( c 为有理数 )
(7)a(c2+1) ____b(c2 +1) ( c 为有理数 )
1
3
1
3
≤
<
D
3.有一道这样的题:“由★x>1得到 x< ”,
则题中★表示的是( )
A.非正数 B.正数
C.非负数 D.负数
4.若 x 比较 2-3x 与2-3y 的大小,并说明理由。
解:∵x<y
∴-3x>-3y
(不等式性质3)
∴2-3x>2-3y
(不等式性质2)
连续递推,豁然开朗
5.小明和小华在探究数学问题.
小明说: “ 3y>4y ”.
小华认为小明说错了,应该是3y<4y,
聪明的你觉得呢
谁做对了
当y>0时, 3y < 4y;
当y= 0时, 3y = 4y;
当y < 0时, 3y >4y.
6.若 x ,且(a-3)x
解:∵x<y, (a-3)x>(a-3)y
∴a-3<0
(不等式性质3)
∴a<3
(不等式性质2)
7.如果 , 那么xy 0.
(依据 )
.
>
不等式的基本性质3
8.如果b<0,你能比较a-b,a+b的大小吗?
a-b>a+b
作差法比较大小:
(a-b)-(a+b)=a-b-a-b=-2b
.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
