3.3 一元一次不等式(1)课件(共19张PPT)
文档属性
| 名称 | 3.3 一元一次不等式(1)课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 423.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 21:04:03 | ||
图片预览




文档简介
(共19张PPT)
性质3:不等式的两边都乘(或都除以)同一个正数,所得到的不等式仍成立;
不等式的两边都乘(或都除以)同一个负数,必须把不等号的方向改变,所得到的不等式成立.
性质1:若a<b,b<c,则a<c。
性质2:不等式的两边都加上(或减去)同一个数,所得到的不等式仍成立.
(不等号方向不变)
(不等号方向不变)
(不等号方向改变)
(不等式传递性)
已知a<b,用“<”“>”填空:
(1)a-3 b-3 (2)6a 6b
(3)-a -b (4)a-b 0
<
<
<
>
齐声朗读:不等式的基本性质
观察下列不等式
(1) x>4 ; (2)3x>30
(3)1.5x+12<0.5x+1 ; (4)
这样的不等式叫做一元一次不等式.
整式,
一次,
不等号的左右两边都是
而且只含有
一个
未知数,
未知数的最高次数是
.
.
1
2
0
3
4
-1
-2
-3
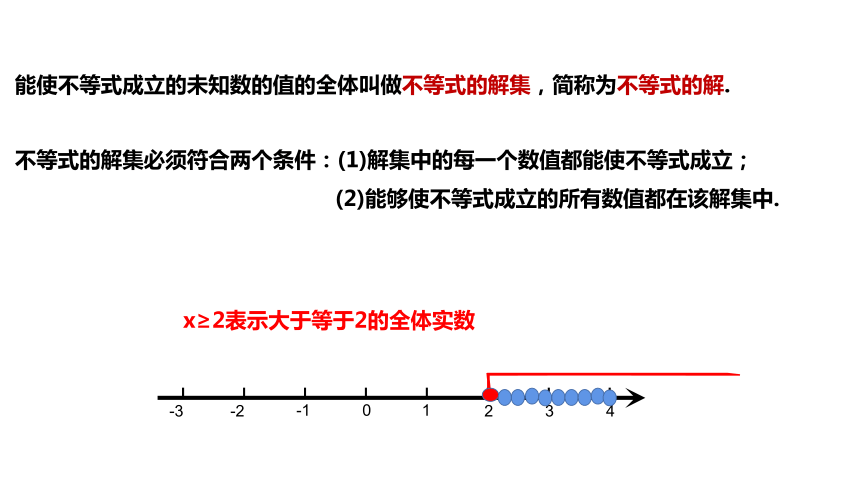
x≥2表示大于等于2的全体实数
能使不等式成立的未知数的值的全体叫做不等式的解集,简称为不等式的解.
不等式的解集必须符合两个条件:(1)解集中的每一个数值都能使不等式成立;
(2)能够使不等式成立的所有数值都在该解集中.
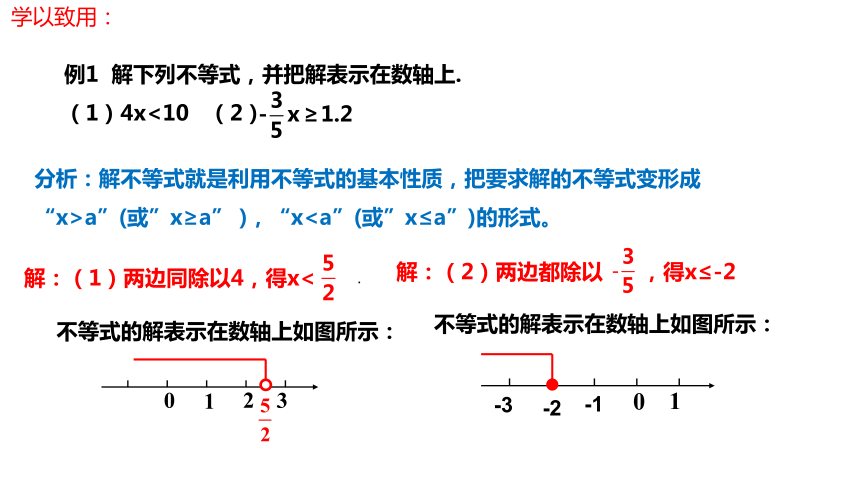
例1 解下列不等式,并把解表示在数轴上.
(1)4x<10 (2)
分析:解不等式就是利用不等式的基本性质,把要求解的不等式变形成“x>a”(或”x≥a” ),“x解:(2)两边都除以 ,得x≤-2
不等式的解表示在数轴上如图所示:
学以致用:
不等式的解表示在数轴上如图所示:
解:(1)两边同除以4,得x<
.
-1
-2
-3
1.下列不等式的解法正确吗?如果不正确,请改正.
(1)-2x<-4
解:两边同除以-2,得______.
(2)x+1>2x-3
解:移项,得4>x,即_______.
X<2
X>4
X>2
X<4
变式:
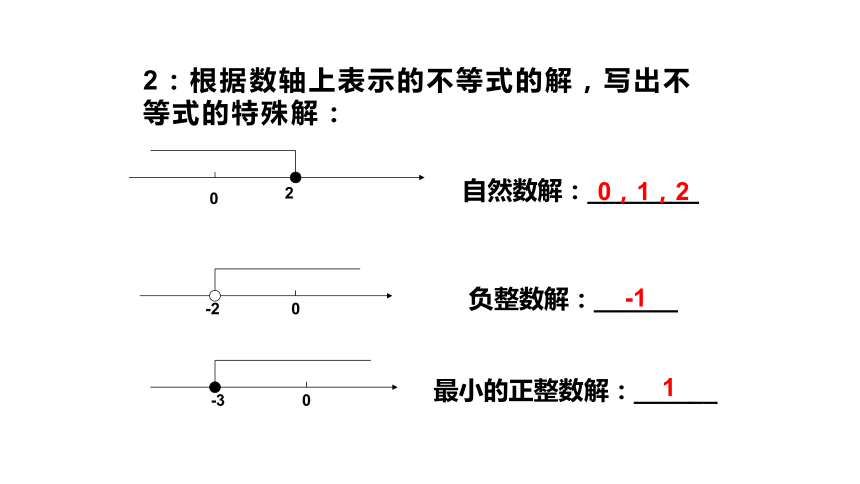
2:根据数轴上表示的不等式的解,写出不等式的特殊解:
自然数解:________
负整数解:______
0
2
0
-2
0
-3
最小的正整数解:______
0,1,2
-1
1
例2 解不等式:
4x-8<12
解:
4x-8+8<12+8.
4x<20.
x<4.
4x<12+8.
移项得:
合并同类项得:
系数化为1:
移项的依据是
不等式性质2
移项 不会使不等号方向发生改变
将不等式一边的项变号后,
移到不等式另一边,
这个过程叫移项
先在不等式的两边同时加8,得
。
由图可得不等式的负整数解是x= -1和x= -2
例3 解不等式7x-2≤9x+3,把解表示在数轴上,并求出不等式的负整数解。
把不等式中的任何一项的符号改变后,从不等号的一边移到另一边,所得到的不等式仍成立.也就是说,在解不等式时,移项法同样适用.
解: 先在不等式的两边同时减去9x,
得7x-2-9x≤9x+3-9x
移项得7x-2-9x≤3
再在不等式的两边同时加上2,
得7x-2-9x+2≤3+2,
移项得7x-9x≤3+2
合并同类项,得-2x≤5
两边同除以-2,
-1
-2
-3
x≥
.
解不等式:
4x-1<5x+15
解方程:
4x-1=5x+15
解:移项,得
4x-5x=15+1
合并同类项,得
-x=16
系数化为1,得
x=-16
解:移项,得
4x-5x<15+1
合并同类项,得
-x<16
系数化为1,得
x>-16
变式:
A
1 下列式子中是一元一次不等式的有( )个
(1)x2+1>2x; (2) ;
(3)4y>6x; (4)7x≥6.
A.1 B.2 C.3 D.4
当堂检测:
夯实基础,稳扎稳打
.
2.解不等式 3-x <2x+6,并把它的解集表示在数轴上.
解:
两边都减2x,得
3-x-2x <2x+6 -2x .
两边都除以-3,得 x>-1.
不等式的解集在数轴上的表示如图:
移项得:3-x-2x <6 .
两边都减3,得
3-x-2x-3<6-3
移项得:-x-2x<6-3
合并同类项,得
-3x <3.
.
1
2
0
3
4
-1
-2
-3
1
3.已知 是关于x的一元一次不等式,
则a的值是________.
x2a-1+10
解析:由 是关于x的一元一次不等式 得2a-1=1,计算即可求出a的值等于1.
x2a-1+10
4.如果x=2是不等式(a-2)x<4a+2的一个解,试 求a的最小整数值.
∴a的最小整数值为-2.
连续递推,豁然开朗
解:由不等式解的意义得:2(a-2)<4a+2
去括号得:2a-4<4a+2
移项得:2a-4a<2+4
合并同类项得:-2a<6
系数化为1得:a>-3
-1
-2
-3
5.解不等式0.5x-3>-14-2.5x,把解表示在数轴上,
并求出适合不等式的最大负整数和最小正整数.
最大负整数解x=-1,最小正整数解x=1
解:0.5x+2.5x , 3x>-11
x>
1
0
-1
-2
-3
-4
6.若(a+1)x>1的解集为x< ,求a的取值范围.
解:∵(a+1)x>1的解集为x< ,
∴a+1<0,
∴a<-1
解得x ≤ 6.
x≤6在数轴上表示如图所示.
-1
0
1
2
3
4
5
6
根据题意,得 ,
由图可知,满足条件的正整数有 1,2,3,4,5,6.
解:
7.当x取什么值时,代数式 的值大于或等于0?并求出所有满足条件的正整数.
.
所以,当x≤6时,代数式
的值大于或等于0.
.
8、若x=3是不等式3a-x≤2x-4的一个解,试求
正整数a的值,并求出此时不等式的解集。
解:把x=3代入不等式得:
3a-3≤6-4
3a≤5
a≤ -
5
3
∴正整数a的值是1
3-x≤2x-4
把a=1代入不等式得:
x≥ -
7
3
∴正整数a的值是1,
原不等式的解集为
x≥ -
7
3
8、若x=3是不等式3a-x≤2x-4的一个解,试求
正整数a的值,并求出此时不等式的解集。
解:把x=3代入不等式得:
3a-3≤6-4
3a≤5
a≤-
5
3
∴正整数a的值是1
3-x≤2x-4
把a=1代入不等式得:
x≥-
7
3
∴正整数a的值是1,
原不等式的解集为
x≥-
7
3
9. 某种光盘的存储容量为670MB,一个文件平均占用空间为13MB,这张光盘能存放52个这样的文件吗?这张光盘最多能存放多少个这样的文件?
解:∵52×13=676>670
∴这张光盘不能存放52个这样的文件.
设这张光盘上存放了x个文件,则
13x≤670
x
∴x的最大整数值为51.
∴这张光盘最多能存放51个这样的文件.
性质3:不等式的两边都乘(或都除以)同一个正数,所得到的不等式仍成立;
不等式的两边都乘(或都除以)同一个负数,必须把不等号的方向改变,所得到的不等式成立.
性质1:若a<b,b<c,则a<c。
性质2:不等式的两边都加上(或减去)同一个数,所得到的不等式仍成立.
(不等号方向不变)
(不等号方向不变)
(不等号方向改变)
(不等式传递性)
已知a<b,用“<”“>”填空:
(1)a-3 b-3 (2)6a 6b
(3)-a -b (4)a-b 0
<
<
<
>
齐声朗读:不等式的基本性质
观察下列不等式
(1) x>4 ; (2)3x>30
(3)1.5x+12<0.5x+1 ; (4)
这样的不等式叫做一元一次不等式.
整式,
一次,
不等号的左右两边都是
而且只含有
一个
未知数,
未知数的最高次数是
.
.
1
2
0
3
4
-1
-2
-3
x≥2表示大于等于2的全体实数
能使不等式成立的未知数的值的全体叫做不等式的解集,简称为不等式的解.
不等式的解集必须符合两个条件:(1)解集中的每一个数值都能使不等式成立;
(2)能够使不等式成立的所有数值都在该解集中.
例1 解下列不等式,并把解表示在数轴上.
(1)4x<10 (2)
分析:解不等式就是利用不等式的基本性质,把要求解的不等式变形成“x>a”(或”x≥a” ),“x
不等式的解表示在数轴上如图所示:
学以致用:
不等式的解表示在数轴上如图所示:
解:(1)两边同除以4,得x<
.
-1
-2
-3
1.下列不等式的解法正确吗?如果不正确,请改正.
(1)-2x<-4
解:两边同除以-2,得______.
(2)x+1>2x-3
解:移项,得4>x,即_______.
X<2
X>4
X>2
X<4
变式:
2:根据数轴上表示的不等式的解,写出不等式的特殊解:
自然数解:________
负整数解:______
0
2
0
-2
0
-3
最小的正整数解:______
0,1,2
-1
1
例2 解不等式:
4x-8<12
解:
4x-8+8<12+8.
4x<20.
x<4.
4x<12+8.
移项得:
合并同类项得:
系数化为1:
移项的依据是
不等式性质2
移项 不会使不等号方向发生改变
将不等式一边的项变号后,
移到不等式另一边,
这个过程叫移项
先在不等式的两边同时加8,得
。
由图可得不等式的负整数解是x= -1和x= -2
例3 解不等式7x-2≤9x+3,把解表示在数轴上,并求出不等式的负整数解。
把不等式中的任何一项的符号改变后,从不等号的一边移到另一边,所得到的不等式仍成立.也就是说,在解不等式时,移项法同样适用.
解: 先在不等式的两边同时减去9x,
得7x-2-9x≤9x+3-9x
移项得7x-2-9x≤3
再在不等式的两边同时加上2,
得7x-2-9x+2≤3+2,
移项得7x-9x≤3+2
合并同类项,得-2x≤5
两边同除以-2,
-1
-2
-3
x≥
.
解不等式:
4x-1<5x+15
解方程:
4x-1=5x+15
解:移项,得
4x-5x=15+1
合并同类项,得
-x=16
系数化为1,得
x=-16
解:移项,得
4x-5x<15+1
合并同类项,得
-x<16
系数化为1,得
x>-16
变式:
A
1 下列式子中是一元一次不等式的有( )个
(1)x2+1>2x; (2) ;
(3)4y>6x; (4)7x≥6.
A.1 B.2 C.3 D.4
当堂检测:
夯实基础,稳扎稳打
.
2.解不等式 3-x <2x+6,并把它的解集表示在数轴上.
解:
两边都减2x,得
3-x-2x <2x+6 -2x .
两边都除以-3,得 x>-1.
不等式的解集在数轴上的表示如图:
移项得:3-x-2x <6 .
两边都减3,得
3-x-2x-3<6-3
移项得:-x-2x<6-3
合并同类项,得
-3x <3.
.
1
2
0
3
4
-1
-2
-3
1
3.已知 是关于x的一元一次不等式,
则a的值是________.
x2a-1+10
解析:由 是关于x的一元一次不等式 得2a-1=1,计算即可求出a的值等于1.
x2a-1+10
4.如果x=2是不等式(a-2)x<4a+2的一个解,试 求a的最小整数值.
∴a的最小整数值为-2.
连续递推,豁然开朗
解:由不等式解的意义得:2(a-2)<4a+2
去括号得:2a-4<4a+2
移项得:2a-4a<2+4
合并同类项得:-2a<6
系数化为1得:a>-3
-1
-2
-3
5.解不等式0.5x-3>-14-2.5x,把解表示在数轴上,
并求出适合不等式的最大负整数和最小正整数.
最大负整数解x=-1,最小正整数解x=1
解:0.5x+2.5x , 3x>-11
x>
1
0
-1
-2
-3
-4
6.若(a+1)x>1的解集为x< ,求a的取值范围.
解:∵(a+1)x>1的解集为x< ,
∴a+1<0,
∴a<-1
解得x ≤ 6.
x≤6在数轴上表示如图所示.
-1
0
1
2
3
4
5
6
根据题意,得 ,
由图可知,满足条件的正整数有 1,2,3,4,5,6.
解:
7.当x取什么值时,代数式 的值大于或等于0?并求出所有满足条件的正整数.
.
所以,当x≤6时,代数式
的值大于或等于0.
.
8、若x=3是不等式3a-x≤2x-4的一个解,试求
正整数a的值,并求出此时不等式的解集。
解:把x=3代入不等式得:
3a-3≤6-4
3a≤5
a≤ -
5
3
∴正整数a的值是1
3-x≤2x-4
把a=1代入不等式得:
x≥ -
7
3
∴正整数a的值是1,
原不等式的解集为
x≥ -
7
3
8、若x=3是不等式3a-x≤2x-4的一个解,试求
正整数a的值,并求出此时不等式的解集。
解:把x=3代入不等式得:
3a-3≤6-4
3a≤5
a≤-
5
3
∴正整数a的值是1
3-x≤2x-4
把a=1代入不等式得:
x≥-
7
3
∴正整数a的值是1,
原不等式的解集为
x≥-
7
3
9. 某种光盘的存储容量为670MB,一个文件平均占用空间为13MB,这张光盘能存放52个这样的文件吗?这张光盘最多能存放多少个这样的文件?
解:∵52×13=676>670
∴这张光盘不能存放52个这样的文件.
设这张光盘上存放了x个文件,则
13x≤670
x
∴x的最大整数值为51.
∴这张光盘最多能存放51个这样的文件.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
