浙教版九年级数学上册第1章二次函数 试卷 (含答案)
文档属性
| 名称 | 浙教版九年级数学上册第1章二次函数 试卷 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 210.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-16 18:26:59 | ||
图片预览




文档简介
浙教版九年级上册二次函数试卷
一、单选题
1.下列函数中,属于二次函数的是( )
A. B.
C. D.
2.二次函数y=x2+4x﹣5的图象的对称轴为( )
A.x=4 B.x=﹣4 C.x=2 D.x=﹣2
3.把抛物线 向右平移 个单位,再向上平移 个单位,得到的抛物线是( )
A. B.
C. D.
4.已知:如图为二次函数y=ax2+bx+c的图象,则一次函数y=ax+b的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.抛物线y=-2x2经过平移到y=-2x2-4x-5,平移方法是( )
A.向左平移1个单位,再向上平移3各单位
B.向左平移1个单位,再向下平移3个单位
C.向右平移1个单位,再向上平移3个单位
D.向右平移1个单位,再向下平移3个单位
6.如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;②4a-2b+c<0;③不等式ax2+bx+c>0的解集是x≥3.5;④若(-2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )
A.①② B.①④ C.①③④ D.②③④
7.下表是二次函数 的 x,y的部分对应值:
则对于该函数的性质的判断:
①该二次函数有最大值; ②不等式y>-1 的解集是x<0 或x>2;③ 方程 的两个实数根分别位于 和 之间;④当x>0 时,函数值y 随x 的增大而增大;
其中正确的是( )
A.②③ B.②④ C.①③ D.①④
8.抛物线 (a,b,c为常数,且 )经过点 和 ,且 ,当 时,y随着x的增大而减小,有下列结论:① ;②若点 ,点 都在抛物线上,则 ;③ .其中,正确结论的个数为( )
A.0 B.1 C.2 D.3
9.在平面直角坐标系中,若点P的橫坐标和纵坐标相等,则称点P为完美点,已知二次函数 (a,b是常数, )的图象上有且只有一个完美点 ,且当 时,函数 的最小值为 ,最大值为1,则m的取值范围是( )
A. B. C. D.
10.已知:如图,正方形ABCD中,AB=2,AC,BD相交于点O,E,F分别为边BC,CD上的动点(点E,F不与线段BC,CD的端点重合)且BE=CF,连接OE,OF,EF.在点E,F运动的过程中,有下列四个结论:
①△OEF是等腰直角三角形;
②△OEF面积的最小值是 ;
③至少存在一个△ECF,使得△ECF的周长是 ;
④四边形OECF的面积是1.
所有正确结论的序号是( )
A.①②③ B.③④ C.①②④ D.①②③④
二、填空题
11.把抛物线 沿x轴向左平移4个单位,再沿y轴向上平移3个单位后,所得新抛物线相应的函数表达式是 .
12.小王想用篱笆围成一个周长为60米的矩形场地,矩形面积S(单位:平方米)随矩形一边长x(单位:米)的变化而变化.则S与x之间的函数关系式是 .(不用写自变量的取值范围)
13.如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=(x﹣1)2﹣4,AB为半圆的直径,则这个“果圆”被y轴截得的弦CD的长为 .
14.“水晶晶南浔”的美食文化中以特有的双交面出名,盛面的瓷碗截面图如图 1 所示,碗体 DEC 呈抛物线状(碗体厚度不计),点 E 是抛物线的顶点,碗底高 EF=1cm,碗底宽 AB=2 cm,当瓷碗中装满面汤时,液面宽 CD=83cm,此时面汤最大深度 EG=6cm,将瓷碗绕点 B 缓缓倾斜倒出部分面汤,如图2,当 LABK=30 时停止,此时液面 CH 到桌面的距离为 cm;碗内面汤的最大深度是 cm.
15.如图.二次函数图象的一部分与x轴的一个交点坐标为,对称轴为直线,结合图象给出下列结论:①;②;③若关于x的一元二次方程的一根是3,则另一根是;④若点,,均在二次函数图象上,则.其中正确的结论的序号为 .
16.如图,已知函数y=ax2+bx+c(a 0)的图象的对称轴经过点(2,0),且与x轴的一个交点坐标为(4,0).下列结论:①b2﹣4ac 0; ②当x 2时,y随x增大而增大; ③a﹣b+c 0;④抛物线过原点;⑤当0 x 4时,y 0.其中结论正确的是 .(填序号)
三、解答题
17.已知抛物线(b是常数)经过点.求该抛物线的解析式和顶点坐标.
18.把二次函数y=x2+bx+c的图象向下平移1个单位长度,再向左平移5个单位长度,所得的抛物线顶点坐标为(﹣3,2),求原抛物线相应的函数表达式.
19.如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.
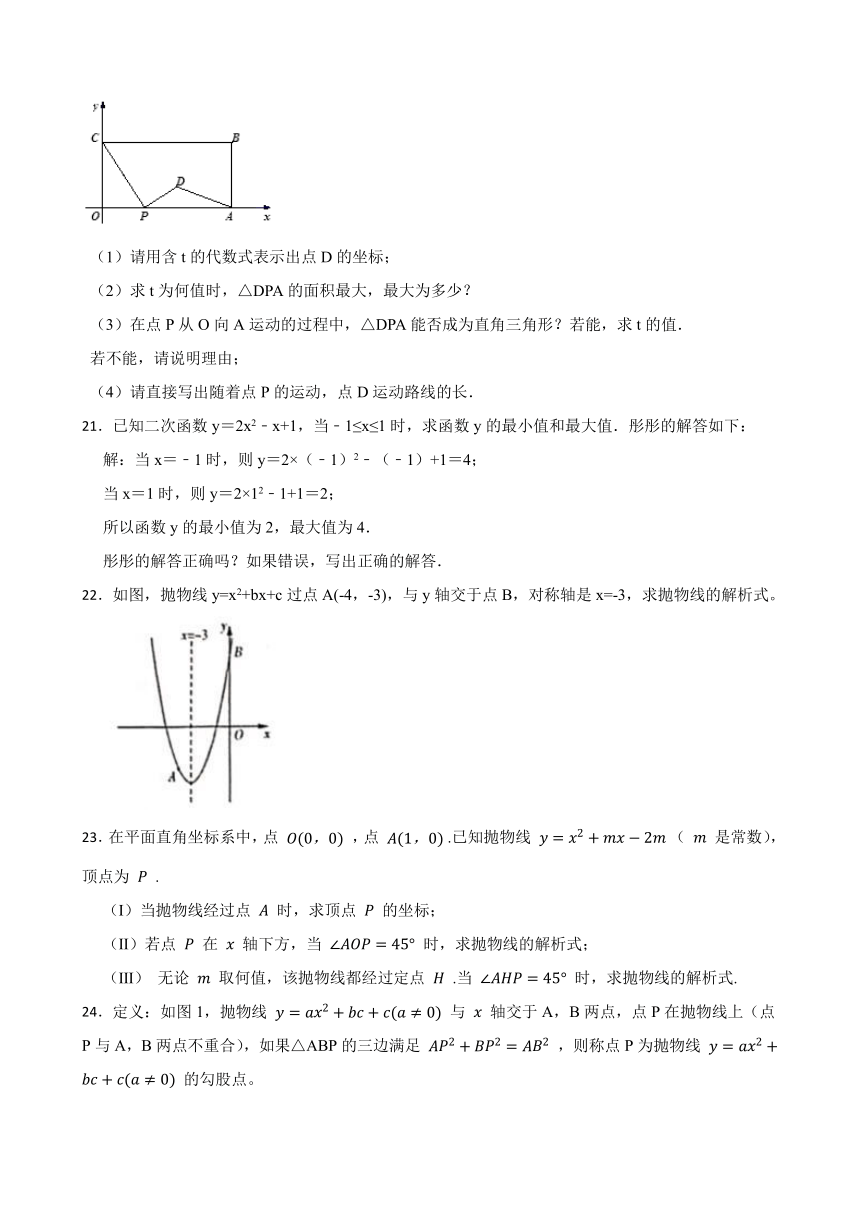
20.如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=2.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.
(1)请用含t的代数式表示出点D的坐标;
(2)求t为何值时,△DPA的面积最大,最大为多少?
(3)在点P从O向A运动的过程中,△DPA能否成为直角三角形?若能,求t的值.
若不能,请说明理由;
(4)请直接写出随着点P的运动,点D运动路线的长.
21.已知二次函数y=2x2﹣x+1,当﹣1≤x≤1时,求函数y的最小值和最大值.彤彤的解答如下:
解:当x=﹣1时,则y=2×(﹣1)2﹣(﹣1)+1=4;
当x=1时,则y=2×12﹣1+1=2;
所以函数y的最小值为2,最大值为4.
彤彤的解答正确吗?如果错误,写出正确的解答.
22.如图,抛物线y=x2+bx+c过点A(-4,-3),与y轴交于点B,对称轴是x=-3,求抛物线的解析式。
23.在平面直角坐标系中,点 ,点 .已知抛物线 ( 是常数),顶点为 .
(Ⅰ)当抛物线经过点 时,求顶点 的坐标;
(Ⅱ)若点 在 轴下方,当 时,求抛物线的解析式;
(Ⅲ) 无论 取何值,该抛物线都经过定点 .当 时,求抛物线的解析式.
24.定义:如图1,抛物线 与 轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足 ,则称点P为抛物线 的勾股点。
(1)直接写出抛物线 的勾股点的坐标;
(2)如图2,已知抛物线C: 与 轴交于A,B两点,点P(1, )是抛物线C的勾股点,求抛物线C的函数表达式;
(3)在(2)的条件下,点Q在抛物线C上,求满足条件 的点Q(异于点P)的坐标
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】A
4.【答案】D
5.【答案】B
6.【答案】B
7.【答案】A
8.【答案】C
9.【答案】C
10.【答案】D
11.【答案】
12.【答案】
13.【答案】3+
14.【答案】;
15.【答案】①②③
16.【答案】①④⑤
17.【答案】解:∵抛物线(b是常数)经过点,
∴把点A坐标代入解析式得,
解得:b=-2,
∴抛物线解析式为:,
把抛物线配方得,
抛物线的顶点坐标为(1,-4).
18.【答案】解:把点(﹣3,2)向上平移1个单位长度,再向右平移5个单位长度后所得对应点的坐标为(2,3),即二次函数图象的顶点坐标为(2,3),
所以原抛物线相应的函数表达式为,即
19.【答案】解:△PBQ的面积S随出发时间t(s)成二次函数关系变化,
∵在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,
动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,
∴BP=12﹣2t,BQ=4t,
∴△PBQ的面积S随出发时间t(s)的解析式为:y= (12﹣2t)×4t=﹣4t2+24t,(0<t<6)
20.【答案】解:(1)∵点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,
∴OP=t,而OC=2,
∴P(t,0),
设CP的中点为F,则F点的坐标为(,1),
∴将线段CP的中点F绕点P按顺时针方向旋转90°得点D,其坐标为(t+1,);
(2)S=
∴当t=2时,S最大,最大值为1
(3)∵∠CPD=900,∴∠DPA+∠CPO=900,∴∠DPA≠900,故有以下两种情况:
①当∠PDA=900时,由勾股定理得,
又,,
,
即t2-4t-12=0,解得t1=2,t2=6(不合题意,舍去)
②当∠PAD=900时,点D在BA上,故AE=3-t,得t=3
综上,经过2秒或3秒时,△PAD是直角三角形;
(4)∵根据点D的运动路线与OB平行且相等,OB=2,
∴点D运动路线的长为2.
21.【答案】解:彤彤的解答错误,
∵
∴二次函数的的对称轴 ,
∵ ,且2>0,
∴当 时,二次函数有最小值 ,
二次函数在 时,y随x增大而减小,二次函数在 时,y随x增大而增大,
∵ ,
∴当 时,二次函数有最大值 ,
∴二次函数的最大值为4,最小值为1.
22.【答案】解:∵对称轴是x= =-3,a=1,
∴b=6
又∵抛物线y=x2+bx+c过点A(-4,-3),
∴(-4)2+6×(-4)+c=-3,解得c=5
∴抛物线的解析式为y=x2+6x+5
23.【答案】解:(Ⅰ)∵抛物线 经过点 ,∴ ,解得 .∴抛物线的解析式为 .∵ ,∴顶点 的坐标为 .(Ⅱ)抛物线 的顶点 的坐标为 .由点 在 轴正半轴上,点 在 轴下方, ,知点 在第四象限.过点 作 轴于点 ,则 .可知 ,即 ,解得 , .当 时,点 不在第四象限,舍去.∴ .∴抛物线解析式为 .(Ⅲ)由 可知,当 时,无论 取何值, 都等于4.得点 的坐标为 .过点 作 ,交射线 于点 ,分别过点 , 作 轴的垂线,垂足分别为 , ,则 .∵ , ,∴ .∴ .∵ ,∴ .∴ .∴ , .可得点 的坐标为 或 .当点 的坐标为 时,可得直线 的解析式为 .∵点 在直线 上,∴ .解得 , .当 时,点 与点 重合,不符合题意,∴ .当点 的坐标为 时,可得直线 的解析式为 .∵点 在直线 上,∴ .解得 (舍), .∴ .综上, 或 .故抛物线解析式为 或
24.【答案】(1)解:勾股点的坐标为(0,1)
(2)解:抛物线y=ax2+bx(a≠0)过原点(0,0),即A(0,0),
如图作PG⊥x轴于点G,连接PA,PB,
∵点P(1,),
∴ AG=1,PG=,
∴PA=2,tan∠PAB=,
∴∠PAB=60°,
∴在Rt△PAB中,AB==4,
∴点B(4,0),
设y=ax(x-4),当x=1时,y=,
解得a=-,
∴y=-x(x-4)=-x2+x.
(3)解:① 当点Q在x轴上方,由S△ABQ=S△ABP,易知点Q的纵坐标为,
∴-x2+x=,解得x1=3,x2=1(不合题意,舍去),
∴Q(3,),
②当点Q在x轴下方,由S△ABQ=S△ABP,易知点Q的纵坐标为-,
∴-x2+x=-,解得x1=2+,x2=2-,
∴Q(2+,-)Q(2-,-),
综上,满足条件的点Q有三个:Q(3,)Q(2+,-)Q(2-,-).
一、单选题
1.下列函数中,属于二次函数的是( )
A. B.
C. D.
2.二次函数y=x2+4x﹣5的图象的对称轴为( )
A.x=4 B.x=﹣4 C.x=2 D.x=﹣2
3.把抛物线 向右平移 个单位,再向上平移 个单位,得到的抛物线是( )
A. B.
C. D.
4.已知:如图为二次函数y=ax2+bx+c的图象,则一次函数y=ax+b的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.抛物线y=-2x2经过平移到y=-2x2-4x-5,平移方法是( )
A.向左平移1个单位,再向上平移3各单位
B.向左平移1个单位,再向下平移3个单位
C.向右平移1个单位,再向上平移3个单位
D.向右平移1个单位,再向下平移3个单位
6.如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;②4a-2b+c<0;③不等式ax2+bx+c>0的解集是x≥3.5;④若(-2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )
A.①② B.①④ C.①③④ D.②③④
7.下表是二次函数 的 x,y的部分对应值:
则对于该函数的性质的判断:
①该二次函数有最大值; ②不等式y>-1 的解集是x<0 或x>2;③ 方程 的两个实数根分别位于 和 之间;④当x>0 时,函数值y 随x 的增大而增大;
其中正确的是( )
A.②③ B.②④ C.①③ D.①④
8.抛物线 (a,b,c为常数,且 )经过点 和 ,且 ,当 时,y随着x的增大而减小,有下列结论:① ;②若点 ,点 都在抛物线上,则 ;③ .其中,正确结论的个数为( )
A.0 B.1 C.2 D.3
9.在平面直角坐标系中,若点P的橫坐标和纵坐标相等,则称点P为完美点,已知二次函数 (a,b是常数, )的图象上有且只有一个完美点 ,且当 时,函数 的最小值为 ,最大值为1,则m的取值范围是( )
A. B. C. D.
10.已知:如图,正方形ABCD中,AB=2,AC,BD相交于点O,E,F分别为边BC,CD上的动点(点E,F不与线段BC,CD的端点重合)且BE=CF,连接OE,OF,EF.在点E,F运动的过程中,有下列四个结论:
①△OEF是等腰直角三角形;
②△OEF面积的最小值是 ;
③至少存在一个△ECF,使得△ECF的周长是 ;
④四边形OECF的面积是1.
所有正确结论的序号是( )
A.①②③ B.③④ C.①②④ D.①②③④
二、填空题
11.把抛物线 沿x轴向左平移4个单位,再沿y轴向上平移3个单位后,所得新抛物线相应的函数表达式是 .
12.小王想用篱笆围成一个周长为60米的矩形场地,矩形面积S(单位:平方米)随矩形一边长x(单位:米)的变化而变化.则S与x之间的函数关系式是 .(不用写自变量的取值范围)
13.如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=(x﹣1)2﹣4,AB为半圆的直径,则这个“果圆”被y轴截得的弦CD的长为 .
14.“水晶晶南浔”的美食文化中以特有的双交面出名,盛面的瓷碗截面图如图 1 所示,碗体 DEC 呈抛物线状(碗体厚度不计),点 E 是抛物线的顶点,碗底高 EF=1cm,碗底宽 AB=2 cm,当瓷碗中装满面汤时,液面宽 CD=83cm,此时面汤最大深度 EG=6cm,将瓷碗绕点 B 缓缓倾斜倒出部分面汤,如图2,当 LABK=30 时停止,此时液面 CH 到桌面的距离为 cm;碗内面汤的最大深度是 cm.
15.如图.二次函数图象的一部分与x轴的一个交点坐标为,对称轴为直线,结合图象给出下列结论:①;②;③若关于x的一元二次方程的一根是3,则另一根是;④若点,,均在二次函数图象上,则.其中正确的结论的序号为 .
16.如图,已知函数y=ax2+bx+c(a 0)的图象的对称轴经过点(2,0),且与x轴的一个交点坐标为(4,0).下列结论:①b2﹣4ac 0; ②当x 2时,y随x增大而增大; ③a﹣b+c 0;④抛物线过原点;⑤当0 x 4时,y 0.其中结论正确的是 .(填序号)
三、解答题
17.已知抛物线(b是常数)经过点.求该抛物线的解析式和顶点坐标.
18.把二次函数y=x2+bx+c的图象向下平移1个单位长度,再向左平移5个单位长度,所得的抛物线顶点坐标为(﹣3,2),求原抛物线相应的函数表达式.
19.如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.
20.如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=2.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.
(1)请用含t的代数式表示出点D的坐标;
(2)求t为何值时,△DPA的面积最大,最大为多少?
(3)在点P从O向A运动的过程中,△DPA能否成为直角三角形?若能,求t的值.
若不能,请说明理由;
(4)请直接写出随着点P的运动,点D运动路线的长.
21.已知二次函数y=2x2﹣x+1,当﹣1≤x≤1时,求函数y的最小值和最大值.彤彤的解答如下:
解:当x=﹣1时,则y=2×(﹣1)2﹣(﹣1)+1=4;
当x=1时,则y=2×12﹣1+1=2;
所以函数y的最小值为2,最大值为4.
彤彤的解答正确吗?如果错误,写出正确的解答.
22.如图,抛物线y=x2+bx+c过点A(-4,-3),与y轴交于点B,对称轴是x=-3,求抛物线的解析式。
23.在平面直角坐标系中,点 ,点 .已知抛物线 ( 是常数),顶点为 .
(Ⅰ)当抛物线经过点 时,求顶点 的坐标;
(Ⅱ)若点 在 轴下方,当 时,求抛物线的解析式;
(Ⅲ) 无论 取何值,该抛物线都经过定点 .当 时,求抛物线的解析式.
24.定义:如图1,抛物线 与 轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足 ,则称点P为抛物线 的勾股点。
(1)直接写出抛物线 的勾股点的坐标;
(2)如图2,已知抛物线C: 与 轴交于A,B两点,点P(1, )是抛物线C的勾股点,求抛物线C的函数表达式;
(3)在(2)的条件下,点Q在抛物线C上,求满足条件 的点Q(异于点P)的坐标
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】A
4.【答案】D
5.【答案】B
6.【答案】B
7.【答案】A
8.【答案】C
9.【答案】C
10.【答案】D
11.【答案】
12.【答案】
13.【答案】3+
14.【答案】;
15.【答案】①②③
16.【答案】①④⑤
17.【答案】解:∵抛物线(b是常数)经过点,
∴把点A坐标代入解析式得,
解得:b=-2,
∴抛物线解析式为:,
把抛物线配方得,
抛物线的顶点坐标为(1,-4).
18.【答案】解:把点(﹣3,2)向上平移1个单位长度,再向右平移5个单位长度后所得对应点的坐标为(2,3),即二次函数图象的顶点坐标为(2,3),
所以原抛物线相应的函数表达式为,即
19.【答案】解:△PBQ的面积S随出发时间t(s)成二次函数关系变化,
∵在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,
动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,
∴BP=12﹣2t,BQ=4t,
∴△PBQ的面积S随出发时间t(s)的解析式为:y= (12﹣2t)×4t=﹣4t2+24t,(0<t<6)
20.【答案】解:(1)∵点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,
∴OP=t,而OC=2,
∴P(t,0),
设CP的中点为F,则F点的坐标为(,1),
∴将线段CP的中点F绕点P按顺时针方向旋转90°得点D,其坐标为(t+1,);
(2)S=
∴当t=2时,S最大,最大值为1
(3)∵∠CPD=900,∴∠DPA+∠CPO=900,∴∠DPA≠900,故有以下两种情况:
①当∠PDA=900时,由勾股定理得,
又,,
,
即t2-4t-12=0,解得t1=2,t2=6(不合题意,舍去)
②当∠PAD=900时,点D在BA上,故AE=3-t,得t=3
综上,经过2秒或3秒时,△PAD是直角三角形;
(4)∵根据点D的运动路线与OB平行且相等,OB=2,
∴点D运动路线的长为2.
21.【答案】解:彤彤的解答错误,
∵
∴二次函数的的对称轴 ,
∵ ,且2>0,
∴当 时,二次函数有最小值 ,
二次函数在 时,y随x增大而减小,二次函数在 时,y随x增大而增大,
∵ ,
∴当 时,二次函数有最大值 ,
∴二次函数的最大值为4,最小值为1.
22.【答案】解:∵对称轴是x= =-3,a=1,
∴b=6
又∵抛物线y=x2+bx+c过点A(-4,-3),
∴(-4)2+6×(-4)+c=-3,解得c=5
∴抛物线的解析式为y=x2+6x+5
23.【答案】解:(Ⅰ)∵抛物线 经过点 ,∴ ,解得 .∴抛物线的解析式为 .∵ ,∴顶点 的坐标为 .(Ⅱ)抛物线 的顶点 的坐标为 .由点 在 轴正半轴上,点 在 轴下方, ,知点 在第四象限.过点 作 轴于点 ,则 .可知 ,即 ,解得 , .当 时,点 不在第四象限,舍去.∴ .∴抛物线解析式为 .(Ⅲ)由 可知,当 时,无论 取何值, 都等于4.得点 的坐标为 .过点 作 ,交射线 于点 ,分别过点 , 作 轴的垂线,垂足分别为 , ,则 .∵ , ,∴ .∴ .∵ ,∴ .∴ .∴ , .可得点 的坐标为 或 .当点 的坐标为 时,可得直线 的解析式为 .∵点 在直线 上,∴ .解得 , .当 时,点 与点 重合,不符合题意,∴ .当点 的坐标为 时,可得直线 的解析式为 .∵点 在直线 上,∴ .解得 (舍), .∴ .综上, 或 .故抛物线解析式为 或
24.【答案】(1)解:勾股点的坐标为(0,1)
(2)解:抛物线y=ax2+bx(a≠0)过原点(0,0),即A(0,0),
如图作PG⊥x轴于点G,连接PA,PB,
∵点P(1,),
∴ AG=1,PG=,
∴PA=2,tan∠PAB=,
∴∠PAB=60°,
∴在Rt△PAB中,AB==4,
∴点B(4,0),
设y=ax(x-4),当x=1时,y=,
解得a=-,
∴y=-x(x-4)=-x2+x.
(3)解:① 当点Q在x轴上方,由S△ABQ=S△ABP,易知点Q的纵坐标为,
∴-x2+x=,解得x1=3,x2=1(不合题意,舍去),
∴Q(3,),
②当点Q在x轴下方,由S△ABQ=S△ABP,易知点Q的纵坐标为-,
∴-x2+x=-,解得x1=2+,x2=2-,
∴Q(2+,-)Q(2-,-),
综上,满足条件的点Q有三个:Q(3,)Q(2+,-)Q(2-,-).
同课章节目录
