【公开课】第1章 二次函数 复习课件(共27张ppt)
文档属性
| 名称 | 【公开课】第1章 二次函数 复习课件(共27张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
第1章 二次函数章末复习
浙教版九年级上册
基础回顾
形如y=ax2+bx+c (a、b、c是常数,a≠0)的函数叫做二次函数
什么叫二次函数
1、它的图象是一条_____;
2、当__时,开口向上;当 时,开口向下;
3、它的对轴是________________
顶点坐标为________________;
与y轴的交点坐标为____________.
抛物线
a>0
-
b
2a
4ac-b2
4a
( )
(0,c)
a<0
直线x=-
b
2a
强化练习
1.下列函数中,哪些是二次函数
是
不是
是
是
不是
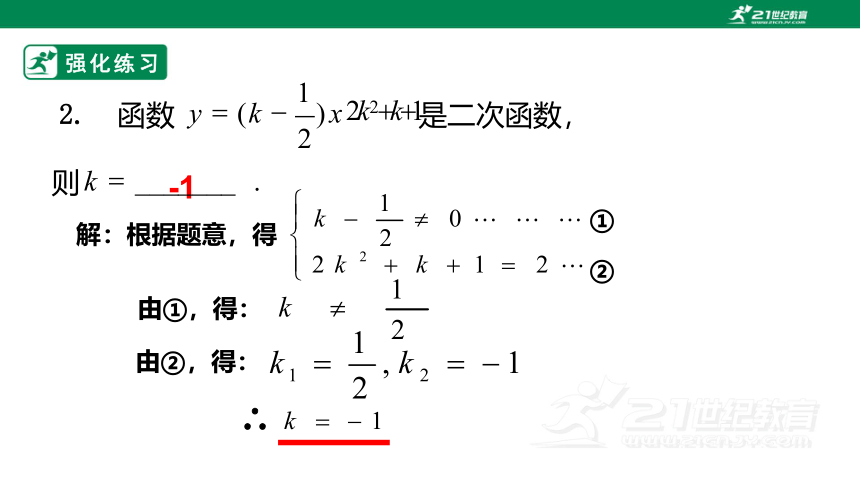
强化练习
①
②
由①,得:
由②,得:
∴
解:根据题意,得
-1
.
_______
)
2
1
(
1
2
=
-
=
+
+
k
x
k
y
k
k2
则
是二次函数,
函数
2.
强化练习
3.抛物线 的顶点坐标是( ).
(A)(-1,-3) (B)(1,3) (C)(-1,8) (D)(1,-8)
4.在同一直角坐标系中,抛物线 与坐标轴的交点个数是( )
(A)0个 (B)1个 (C)2个 (D)3个
D
C
基础回顾
2、已知抛物线顶点坐标(m, k),通常设抛物线解析式为_______________
3、已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________________
1、已知抛物线上的三点,通常设解析式为________________
y=ax2+bx+c(a≠0)
y=a(x-m)2+k(a≠0)
y=a(x-x1)(x-x2) (a≠0)
求抛物线解析式常用的三种方法
一般式
顶点式
交点式或两根式
强化练习
6.抛物线y=x2+bx+c ,经过A(-1,0),B(3,0)两点,则这条抛物线的解析式是 ,它的对称轴是 。
7.已知二次函数的图像的顶点坐标为(-2,-3),且图像经过点(-3,-2),求这条抛物线的解析式是:________________
注意: 根据已知点的特点,选取合理的二次函数解析式能 给我们的计算带来简便
典例讲解
例1.二次函数的图象经过A(1,0) B(3,0) C(2,-1)三点,
(1)求这个函数的解析式.
(2)求函数与直线 y=2x+1 的交点坐标 .
解:(1)设这个函数的解析式为 y=ax2+bx+c, 依题意得:
解这个方程组得
∴这个函数的解析式是:y=x2-4x+3
解这个方程组得:
∴函数与直线的交点坐标是:(1,0) (2,-1)
(2)
还可以怎么求解析式?
基础回顾
二次函数图象
对称轴
顶点坐标
最值
增减性
y=ax2
y=a(x+m)2
y=a(x+m)2+k
y=ax2+bx+c
y=ax2+k
顶点式
一般式
配方
平移
直线x=0
直线x=-m
直线x=-m
(0,0)
(-m,0)
(-m,k)
a>0当x=0,y最小=0
a>0当x=-m,y最小=0
a>0当x=-m,y最小=k
a>0,x≤-m,y随x增大而减小 x≥-m,y随x增大而增大
a>0,x≤-b/2a,y随x增大而减小 x≥-b/2a,y随x增大而增大
直线x=-
b
2a
-
b
2a
4ac-b2
4a
( )
强化练习
(1) y=2(x+2)2是由 向 平移 个单位得到
(3) y=-2x2-2是由 向 平移 个单位得到
(3) y=-2(x-2)2+3是由 向 平移 个单位
,再向 平移 个单位得到
(4) y=2x2+4x-5是由 向 平移 个单位,再向 平移 个单位得到
(5) y=2x2向左平移2个单位,再向下平移3个单位得到
函数解析式是 。
y=2(x+2)2-3
y=2x2
左
2
y=-2x2
下
2
y=-2x2
右
2
上
3
y=2x2
左
1
下
7
8.完成下列填空:
强化练习
(6)由函数y= -3(x-1)2+2的图象向右平移4个单位,再向上平移3个单位,得到的图象的函数解析式为_________________
y= - 3(x-1-4)2+2+3
(7)抛物线y=ax2向左平移一个单位,再向下平移8个单位且y=ax2过点(1,2).则平移后的解析式为______________;
y=2(x+1)2-8
(8)将抛物线y=x2-6x+4如何移动才能得到y=x2.
逆向思考,由y=x2-6x+4 =(x-3)2-5知:先向左平移3个单位,再向上平移5个单位.
8.完成下列填空:
基础回顾
如何判别a、b、c、b2-4ac,2a+b,a+b+c的符号
(1)a的符号:
由抛物线的开口方向确定
开口向上
a>0
开口向下
a<0
(2)C的符号:
由抛物线与y轴的交点位置确定.
交点在x轴上方
c>0
交点在x轴下方
c<0
经过坐标原点
c=0
基础回顾
(3)b的符号:
由对称轴的位置确定
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴
b=0
(4)b2-4ac的符号:
由抛物线与x轴的交点个数确定
与x轴有两个交点
b2-4ac>0
与x轴有一个交点
b2-4ac=0
与x轴无交点
b2-4ac<0
强化练习
9. 已知y=ax2+bx+c的图象如图所示,完成下列填空:
a___0, b____0, c_____0, abc____0
b2-4ac_____0
a+b+c_____0, a-b+c____0
4a-2b+c_____0
0
-1
1
-2
<
<
<
>
>
>
>
>
课堂练习
x
y
O
A
x
y
O
B
x
y
O
C
x
y
O
D
10.在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为( )
B
强化练习
11.已知:二次函数y=ax2+bx+c的图象如图所示,则点M( ,a)在( )
A、第一象限
B、第二象限
C、第三象限
D、第四象限
x
o
y
D
强化练习
12.如图1所示,二次函数y=ax2+bx+c的图像开口向上,图像经过点(-1,2)和(1,0)且与y轴交于负半轴.
第(1)问:给出四个结论:①a>0;②b>0;③c>0;④a+b+c=0,其中正确的结论的序号是 .
第(2)问:给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.其中正确的结论的序号是_______.
思路点拨:
本题考查同学们的识图能力.
①④
②③④
第(1)问中观察函数图像得:
图像开口向上决定a>0;
对称轴 >0,可得b<0;
x=0时, y<0,即c <0;
由x=1时,y=0,得a+b+c=0.
第(2)问要求我们具有一定推理能力.
由(1)知a>0,b<0,c<0;∴abc>0;
又对称轴 <1, ∴2a+b > 0;
∵(-1,2),(1,0)在抛物线上,
代入解析式得
①+②得a+c=1,得a=1-c,∵c < 0∴1-c > 1,即a > 1.
强化练习
二次函数与一元二次方程
13、函数y=ax2-ax+3x+1的图象与x轴有且只有一个交点,那么a的值和交点坐标分别为 。
9或1
14、根据下列表格的对应值:
判断方程ax2+bx+c=0(a≠0,a、b、c为常数)一个解的范围是 ( )
A、3<x<3.23 B、3.23<x<3.24
C、3.24<x<3.25 D、3.25<x<3.26
x 3.23 3.24 3.25 3.26
y=ax2+bx+c -0.06 -0.02 0.03 0.09
C
综合提高
二次函数的实际问题
问题2这位同学身高1.7 m,若在这次跳投中,球在头顶上方0.25 m处出手,问:球出手时,他跳离地面的高度是多少?
x
y
o
例2、如图,有一次,我班某同学在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离2.5m时,达到最大高度3.5m,然后准确落入篮圈。已知篮圈中心到地面的距离为3.05m.
3.05 m
2.5m
3.5m
问题1 建立如图所示的直角坐标系,求抛物线的解析式;
4 m
强化练习
二次函数的实际问题
15.你知道吗?平时我们在跳绳时,绳甩到最高处的形状可近似的看为抛物线,如图所示,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1米、2.5米处,绳子甩到最高处时,刚好通过他们的头顶,已知学生丙的身高是1.5米,请你算一算学生丁的身高。
1m
2.5m
4m
1m
甲
乙
丙
丁
x
y
o
(0,1)
(4,1)
(1,1.5)
综合提高
二次函数的实际问题
例3、某商人如果将进货单价为8元的商品按每件10元出售,每天可销售100件,现在他采用提高出售价格,减少进货量的办法增加利润,已知这种商品每涨价一元,其销售量将减少10件,问他将出售价定为多少元时,才能使每天所获利润最大?并且求出最大利润是多少?
解:设利润为y元,售价为x元,则每天可销售100-10(x-10)件,依题意得:
y=(x-8)([100-10(x-10)]
化简得 y= -10x2-280x -1600
配方得y= -10(x-14)2 + 360
∴当 (x-14)2 =0时,即x=14时,y 有最大值是360
答:当定价为14元时,所获利润最大,最大利润是360元。
综合提高
二次函数与几何问题
例4、已知二次函数 。
(1)求证:不论a为何实数,此函数图象与x轴总有两个交点。
(2)设a<0,当此函数图象与x轴的两个交点的距离为 时,求出此二次函数的解析式。
(3)在(2)中的二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为 ,若存在求出P点坐标,若不存在请说明理由。
(1)证明:
总结提高
说说这节课的收获和体验
让大家与你分享
一个定义: 二次函数
两个关系:
抛物线与a,b,c关系
抛物线间的平移关系
三个表达式:
一般式
顶点式
两根式
y=ax2+bx+c(a≠0)
y=a(x-x1)(x-x2) (a≠0)
y=a(x-h)2+k(a≠0)
数形结合思想
函数思想
两个思想:
能力提升
1、如图,用40m长的篱笆围一个矩形,其中一边靠墙,设矩形ABCD的边BC=x(m),则面积为y(m2)。当矩形ABCD的边BC为多长时,所围成的矩形面积最大?最大面积是多少?
:
解
y=
(
x
)
=
=20x-
=
-
+
20x
a=-
b=20 c=0
当
=-
=20时
y=
=
=200
所以当BC=x=20 m时
矩形ABCD的面积最大,最大面积是200m2
能力提升
2、已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同,顶点在直线x=1上,且顶点到x轴的距离为5,请写出满足此条件的抛物线的解析式.
解: 抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同
a=1或-1
又 顶点在直线x=1上,且顶点到x轴的距离为5,
顶点为(1,5)或(1,-5)
所以其解析式为:
(1) y=(x-1)2+5 (2) y=(x-1)2-5
(3) y=-(x-1)2+5 (4) y=-(x-1)2-5
展开成一般式即可.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第1章 二次函数章末复习
浙教版九年级上册
基础回顾
形如y=ax2+bx+c (a、b、c是常数,a≠0)的函数叫做二次函数
什么叫二次函数
1、它的图象是一条_____;
2、当__时,开口向上;当 时,开口向下;
3、它的对轴是________________
顶点坐标为________________;
与y轴的交点坐标为____________.
抛物线
a>0
-
b
2a
4ac-b2
4a
( )
(0,c)
a<0
直线x=-
b
2a
强化练习
1.下列函数中,哪些是二次函数
是
不是
是
是
不是
强化练习
①
②
由①,得:
由②,得:
∴
解:根据题意,得
-1
.
_______
)
2
1
(
1
2
=
-
=
+
+
k
x
k
y
k
k2
则
是二次函数,
函数
2.
强化练习
3.抛物线 的顶点坐标是( ).
(A)(-1,-3) (B)(1,3) (C)(-1,8) (D)(1,-8)
4.在同一直角坐标系中,抛物线 与坐标轴的交点个数是( )
(A)0个 (B)1个 (C)2个 (D)3个
D
C
基础回顾
2、已知抛物线顶点坐标(m, k),通常设抛物线解析式为_______________
3、已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________________
1、已知抛物线上的三点,通常设解析式为________________
y=ax2+bx+c(a≠0)
y=a(x-m)2+k(a≠0)
y=a(x-x1)(x-x2) (a≠0)
求抛物线解析式常用的三种方法
一般式
顶点式
交点式或两根式
强化练习
6.抛物线y=x2+bx+c ,经过A(-1,0),B(3,0)两点,则这条抛物线的解析式是 ,它的对称轴是 。
7.已知二次函数的图像的顶点坐标为(-2,-3),且图像经过点(-3,-2),求这条抛物线的解析式是:________________
注意: 根据已知点的特点,选取合理的二次函数解析式能 给我们的计算带来简便
典例讲解
例1.二次函数的图象经过A(1,0) B(3,0) C(2,-1)三点,
(1)求这个函数的解析式.
(2)求函数与直线 y=2x+1 的交点坐标 .
解:(1)设这个函数的解析式为 y=ax2+bx+c, 依题意得:
解这个方程组得
∴这个函数的解析式是:y=x2-4x+3
解这个方程组得:
∴函数与直线的交点坐标是:(1,0) (2,-1)
(2)
还可以怎么求解析式?
基础回顾
二次函数图象
对称轴
顶点坐标
最值
增减性
y=ax2
y=a(x+m)2
y=a(x+m)2+k
y=ax2+bx+c
y=ax2+k
顶点式
一般式
配方
平移
直线x=0
直线x=-m
直线x=-m
(0,0)
(-m,0)
(-m,k)
a>0当x=0,y最小=0
a>0当x=-m,y最小=0
a>0当x=-m,y最小=k
a>0,x≤-m,y随x增大而减小 x≥-m,y随x增大而增大
a>0,x≤-b/2a,y随x增大而减小 x≥-b/2a,y随x增大而增大
直线x=-
b
2a
-
b
2a
4ac-b2
4a
( )
强化练习
(1) y=2(x+2)2是由 向 平移 个单位得到
(3) y=-2x2-2是由 向 平移 个单位得到
(3) y=-2(x-2)2+3是由 向 平移 个单位
,再向 平移 个单位得到
(4) y=2x2+4x-5是由 向 平移 个单位,再向 平移 个单位得到
(5) y=2x2向左平移2个单位,再向下平移3个单位得到
函数解析式是 。
y=2(x+2)2-3
y=2x2
左
2
y=-2x2
下
2
y=-2x2
右
2
上
3
y=2x2
左
1
下
7
8.完成下列填空:
强化练习
(6)由函数y= -3(x-1)2+2的图象向右平移4个单位,再向上平移3个单位,得到的图象的函数解析式为_________________
y= - 3(x-1-4)2+2+3
(7)抛物线y=ax2向左平移一个单位,再向下平移8个单位且y=ax2过点(1,2).则平移后的解析式为______________;
y=2(x+1)2-8
(8)将抛物线y=x2-6x+4如何移动才能得到y=x2.
逆向思考,由y=x2-6x+4 =(x-3)2-5知:先向左平移3个单位,再向上平移5个单位.
8.完成下列填空:
基础回顾
如何判别a、b、c、b2-4ac,2a+b,a+b+c的符号
(1)a的符号:
由抛物线的开口方向确定
开口向上
a>0
开口向下
a<0
(2)C的符号:
由抛物线与y轴的交点位置确定.
交点在x轴上方
c>0
交点在x轴下方
c<0
经过坐标原点
c=0
基础回顾
(3)b的符号:
由对称轴的位置确定
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴
b=0
(4)b2-4ac的符号:
由抛物线与x轴的交点个数确定
与x轴有两个交点
b2-4ac>0
与x轴有一个交点
b2-4ac=0
与x轴无交点
b2-4ac<0
强化练习
9. 已知y=ax2+bx+c的图象如图所示,完成下列填空:
a___0, b____0, c_____0, abc____0
b2-4ac_____0
a+b+c_____0, a-b+c____0
4a-2b+c_____0
0
-1
1
-2
<
<
<
>
>
>
>
>
课堂练习
x
y
O
A
x
y
O
B
x
y
O
C
x
y
O
D
10.在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为( )
B
强化练习
11.已知:二次函数y=ax2+bx+c的图象如图所示,则点M( ,a)在( )
A、第一象限
B、第二象限
C、第三象限
D、第四象限
x
o
y
D
强化练习
12.如图1所示,二次函数y=ax2+bx+c的图像开口向上,图像经过点(-1,2)和(1,0)且与y轴交于负半轴.
第(1)问:给出四个结论:①a>0;②b>0;③c>0;④a+b+c=0,其中正确的结论的序号是 .
第(2)问:给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.其中正确的结论的序号是_______.
思路点拨:
本题考查同学们的识图能力.
①④
②③④
第(1)问中观察函数图像得:
图像开口向上决定a>0;
对称轴 >0,可得b<0;
x=0时, y<0,即c <0;
由x=1时,y=0,得a+b+c=0.
第(2)问要求我们具有一定推理能力.
由(1)知a>0,b<0,c<0;∴abc>0;
又对称轴 <1, ∴2a+b > 0;
∵(-1,2),(1,0)在抛物线上,
代入解析式得
①+②得a+c=1,得a=1-c,∵c < 0∴1-c > 1,即a > 1.
强化练习
二次函数与一元二次方程
13、函数y=ax2-ax+3x+1的图象与x轴有且只有一个交点,那么a的值和交点坐标分别为 。
9或1
14、根据下列表格的对应值:
判断方程ax2+bx+c=0(a≠0,a、b、c为常数)一个解的范围是 ( )
A、3<x<3.23 B、3.23<x<3.24
C、3.24<x<3.25 D、3.25<x<3.26
x 3.23 3.24 3.25 3.26
y=ax2+bx+c -0.06 -0.02 0.03 0.09
C
综合提高
二次函数的实际问题
问题2这位同学身高1.7 m,若在这次跳投中,球在头顶上方0.25 m处出手,问:球出手时,他跳离地面的高度是多少?
x
y
o
例2、如图,有一次,我班某同学在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离2.5m时,达到最大高度3.5m,然后准确落入篮圈。已知篮圈中心到地面的距离为3.05m.
3.05 m
2.5m
3.5m
问题1 建立如图所示的直角坐标系,求抛物线的解析式;
4 m
强化练习
二次函数的实际问题
15.你知道吗?平时我们在跳绳时,绳甩到最高处的形状可近似的看为抛物线,如图所示,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1米、2.5米处,绳子甩到最高处时,刚好通过他们的头顶,已知学生丙的身高是1.5米,请你算一算学生丁的身高。
1m
2.5m
4m
1m
甲
乙
丙
丁
x
y
o
(0,1)
(4,1)
(1,1.5)
综合提高
二次函数的实际问题
例3、某商人如果将进货单价为8元的商品按每件10元出售,每天可销售100件,现在他采用提高出售价格,减少进货量的办法增加利润,已知这种商品每涨价一元,其销售量将减少10件,问他将出售价定为多少元时,才能使每天所获利润最大?并且求出最大利润是多少?
解:设利润为y元,售价为x元,则每天可销售100-10(x-10)件,依题意得:
y=(x-8)([100-10(x-10)]
化简得 y= -10x2-280x -1600
配方得y= -10(x-14)2 + 360
∴当 (x-14)2 =0时,即x=14时,y 有最大值是360
答:当定价为14元时,所获利润最大,最大利润是360元。
综合提高
二次函数与几何问题
例4、已知二次函数 。
(1)求证:不论a为何实数,此函数图象与x轴总有两个交点。
(2)设a<0,当此函数图象与x轴的两个交点的距离为 时,求出此二次函数的解析式。
(3)在(2)中的二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为 ,若存在求出P点坐标,若不存在请说明理由。
(1)证明:
总结提高
说说这节课的收获和体验
让大家与你分享
一个定义: 二次函数
两个关系:
抛物线与a,b,c关系
抛物线间的平移关系
三个表达式:
一般式
顶点式
两根式
y=ax2+bx+c(a≠0)
y=a(x-x1)(x-x2) (a≠0)
y=a(x-h)2+k(a≠0)
数形结合思想
函数思想
两个思想:
能力提升
1、如图,用40m长的篱笆围一个矩形,其中一边靠墙,设矩形ABCD的边BC=x(m),则面积为y(m2)。当矩形ABCD的边BC为多长时,所围成的矩形面积最大?最大面积是多少?
:
解
y=
(
x
)
=
=20x-
=
-
+
20x
a=-
b=20 c=0
当
=-
=20时
y=
=
=200
所以当BC=x=20 m时
矩形ABCD的面积最大,最大面积是200m2
能力提升
2、已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同,顶点在直线x=1上,且顶点到x轴的距离为5,请写出满足此条件的抛物线的解析式.
解: 抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同
a=1或-1
又 顶点在直线x=1上,且顶点到x轴的距离为5,
顶点为(1,5)或(1,-5)
所以其解析式为:
(1) y=(x-1)2+5 (2) y=(x-1)2-5
(3) y=-(x-1)2+5 (4) y=-(x-1)2-5
展开成一般式即可.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
