2022-2023学年浙教版九年级数学上册 圆的有关计算讲义(无答案)
文档属性
| 名称 | 2022-2023学年浙教版九年级数学上册 圆的有关计算讲义(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 206.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-16 20:05:58 | ||
图片预览




文档简介
数学学科学生讲义
学生姓名: 年 级:九年级 科目:数学 学科教师:
课题 圆的有关计算
授课类型 基础知识 典型例题 巩固提升
教学目标 会计算弧长,能计算扇形的面积; 掌握正多边形的有关概念,会计算正多边形的外接圆、内接圆半径。
教学重难点 灵活应用弧长公式、扇形面积公式; 会计算正多边形的外接圆、内接圆半径。
授课日期及时段
教学内容
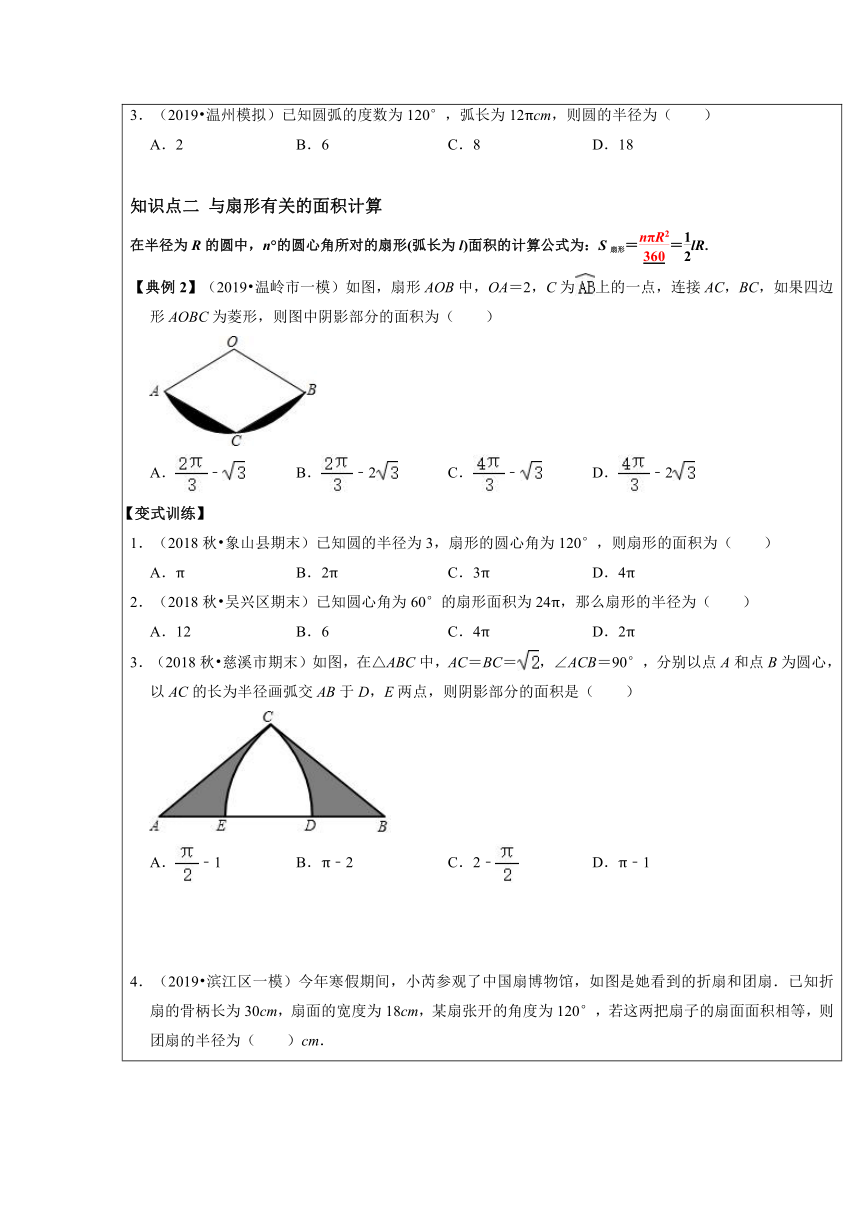
知识点一 弧长的计算 在半径为R的圆中,n°的圆心角所对的弧长l的计算公式为:l=. 【典例1】(2019秋 鹿城区校级月考)如图,在4×4的正方形网格中,若将△ABC绕着点A逆时针旋转得到△AB′C′,则的长为( ) A.π B. C.7 D.6 【变式训练】 1.(2019秋 庆云县期中)已知圆的半径为3,扇形的圆心角为120°,则扇形的弧长为( ) A.π B.2π C.3π D.4 2.(2019春 萧山区月考)如果一个扇形的半径是3,弧长是π,那么此扇形的圆心角的大小为( ) A.30° B.45° C.60° D.90° 3.(2019 温州模拟)已知圆弧的度数为120°,弧长为12πcm,则圆的半径为( ) A.2 B.6 C.8 D.18 知识点二 与扇形有关的面积计算 在半径为R的圆中,n°的圆心角所对的扇形(弧长为l)面积的计算公式为:S扇形==lR. 【典例2】(2019 温岭市一模)如图,扇形AOB中,OA=2,C为上的一点,连接AC,BC,如果四边形AOBC为菱形,则图中阴影部分的面积为( ) A.﹣ B.﹣2 C.﹣ D.﹣2 【变式训练】 1.(2018秋 象山县期末)已知圆的半径为3,扇形的圆心角为120°,则扇形的面积为( ) A.π B.2π C.3π D.4π 2.(2018秋 吴兴区期末)已知圆心角为60°的扇形面积为24π,那么扇形的半径为( ) A.12 B.6 C.4π D.2π 3.(2018秋 慈溪市期末)如图,在△ABC中,AC=BC=,∠ACB=90°,分别以点A和点B为圆心,以AC的长为半径画弧交AB于D,E两点,则阴影部分的面积是( ) A.﹣1 B.π﹣2 C.2﹣ D.π﹣1 4.(2019 滨江区一模)今年寒假期间,小芮参观了中国扇博物馆,如图是她看到的折扇和团扇.已知折扇的骨柄长为30cm,扇面的宽度为18cm,某扇张开的角度为120°,若这两把扇子的扇面面积相等,则团扇的半径为( )cm. A.6 B.8 C.6 D.8 知识点三 正多边形的相关计算 1.正多边形的中心:正多边形的外接圆的圆心.外接圆的半径叫做正多边形的半径,正多边形每一边所对的圆心角叫做正多边形的中心角,中心到正多边形的一边的距离叫做正多边形的边心距.作相等的圆心角就可以等分圆周,从而得到相应正多边形. 2.每个正多边形都有一个外接圆和一个内切圆,正多边形的边心距就是内切圆的半径.研究正多边形往往构造等腰三角形,并结合勾股定理、三角函数等解决. 【典例3】(2018秋 萧山区期末)边长为2的正方形内接于⊙O,则⊙O的半径是( ) A.1 B. C.2 D.2 【变式训练】 1.如图,已知正五边形ABCDE内接于⊙O,连结BD,则∠ABD的度数是( ) A.60° B.70° C.72° D.144° 2.如图,⊙O是正六边形ABCDEF的外接圆,P是弧EF上一点,则∠BPD的度数是( ) A.30° B.60° C.55° D.75° (2019秋 慈溪市期中)已知⊙O的半径为1,则其内接正六边形的边长为 . 4.(2019 海宁市一模)如图,已知点O是正六边形ABCDEF的对称中心,G,H分别是AF,BC上的点,且AG=BH. (1)求∠FAB的度数; (2)求证:OG=OH. 课堂训练 (2019秋 萧山区期中)正方形ABCD是半径为10的圆内接正方形,则正方形的周长为 . 2.(2019 温州一模)已知一扇形的半径长是4,圆心角为60°,则这个扇形的面积为 . 3.(2019秋 镇海区校级期中)半径为9的圆中,120度的圆心角所对的弧长是( ) A.4π B.5π C.6π D.8π 4.(2018秋 温岭市期末)在⊙O中,60°的圆心角所对的弧长是3π,则⊙O的半径是( ) A.9 B.18 C.9π D.18π 5.(2019秋 江干区校级月考)如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为 (计算结果保留π) 6.(2019秋 瑞安市期中)如图,在边长为2的正方形ABCD中,点E是边CD的中点,以A为圆心,AB为半径作弧,交BE于点F.记图中分割部分的面积为S1,S2,则S1﹣S2的值为( ) A.4﹣π B.2π﹣4 C.6﹣2π D.π﹣3 7.(2018秋 吴兴区期末)如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC. (1)求证:AE=ED; (2)若AB=8,∠CBD=30°,求图中阴影部分的面积. 8.(2018 温州校级月考)如图,在⊙O中,弦AB=弦CD,AB⊥CD于点E,且AE<EB,CE<ED,连结AO,DO,BD. (1)求证:EB=ED. (2)若AO=6,求的长. 一、选择题 1.(2019 温州)若扇形的圆心角为90°,半径为6,则该扇形的弧长为( ) A.π B.2π C.3π D.6π 2.(2019秋 慈溪市期中)钟面上的分针的长为1,从9点到9点15分,分针在钟面上扫过的面积是( ) A.π B.π C. D.π 3.(2018秋 杭州期末)已知圆心角为120°的扇形的弧长为6π,该扇形的面积为( ) A.18π B.27π C.36π D.54π 4.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则劣弧AC的长( ) A.2π B.π C. D.4π 5.(2019秋 萧山区期中)如图,点C是以AB为直径的半圆O的三等分点,AC=2,则图中阴影部分的面积是( ) A. B. C. D. 6.(2019秋 苍南县期中)三个正方形方格在扇形中的位置如图所示,点O为扇形的圆心,格点A,B,C分别在扇形的两条半径和弧上,已知每个方格的边长为1,则的长为( ) A.πcm B. C. D.2πcm 7.(2018秋 吴兴区期末)如图,探究:用6个小正方形构造如图所示的网格图(每个小正方形的边长均为2),设经过图中M、P、H三点的圆弧与AH交于R,则弧HR的弧长为( ) A. B.π C.π D.π 8.(2018秋 黄岩区期末)如图,圆P的半径为10,A、B是圆上任意两点,且AB=12,以AB为边作正方形ABCD(点D、P在直线AB的两侧),若AB边绕点P旋转一周,则CD边扫过的面积为( ) A.0 B.36π C. D.6π 9.(2018秋 椒江区期末)如图,在半径为6cm的⊙O中,点A是劣弧的中点,点D是优弧上一点,且∠D=30°,下列四个结论:①OA⊥BC;②BC=3cm;③扇形OCAB的面积为12π;④四边形ABOC是菱形.其中正确结论的序号是( ) ①③ B.①②③④ C.②③④ D.①③④ 10.(2019 乐清市模拟)如图,半径为3的扇形AOB,∠AOB=120°,以AB为边作矩形ABCD交弧AB于点E,F,且点E,F为弧AB的四等分点,矩形ABCD与弧AB形成如图所示的三个阴影区域,其面积分别为S1,S2,S3,则S1+S3﹣S2为( )(π取3) A. B.+ C.﹣ D. 二、填空题 11.(2019 鹿城区校级一模)如图,已知扇形的圆心角∠AOB=120°,半径OA=2,则扇形的弧长为 _______. 12.(2019秋 鹿城区校级月考)扇形的圆心角是30°.它的半径是6,则扇形的面积是 (结果保留π). 13.(2019秋 秀洲区期中)已知扇形的圆心角为120°,面积为27πcm2,则该扇形所在圆的半径为 . 14.(2018秋 慈溪市期末)如图,A,B,C是⊙O上三点,若∠ABC=120°,⊙O的半径为2,则劣弧AC的长为 . 15.(2018 椒江区模拟)如图,有一个正六边形图片,每组平行的对边距离为3米,点A是正六边形的一个顶点,现点A与数轴的原点O重合,工人将图片沿数轴正方向滚动一周,点A恰好落在数轴点A′上,则点A′对应的实数是 . 16.(2018 路桥区一模)如图,在圆内画正六边形、正五边形,则∠ABC= . 17.(2018秋 滨江区期末)如图,⊙O的半径为6,MN为直径,AB,CD为弦,且AB∥MN∥CD,与的度数和为150°,则图中两块阴影部分面积和为 . 三、解答题 18.(2019 上城区一模)如图,在△ABC中,AB=AC,以边BC为直径的⊙O与边AB交于点D,与边AC交于点E,连结OD,OE. (1)求证:BD=CE. (2)若∠C=55°,BC=10,求扇形DOE的面积. 19.(2018秋 柯桥区期末)如图,在△ABC中,AB=AC,以AB为直径的圆,交AC于E点,交BC于D点. (1)若AB=8,∠C=60°,求阴影部分的面积; (2)当∠A为锐角时,试说明∠A与∠CBE的关系. 20.(2019秋 瑞安市期中)如图,在⊙O中,弦AB⊥弦CD于点E,弦AG⊥弦BC于点F,AG与CD相交于点M. (1)求证:=; (2)若弧=80°,⊙O的半径为6,求+的弧长和. 21.(2019秋 宁海县期中)如图,已知AB是⊙O的直径,C、D是⊙O上的点,OC∥BD,交AD于点E,连结BC. (1)求证:AE=ED; (2)若AB=10,∠CBD=36°,求弧AC的长及扇形AOC的面积. 22.(2019秋 苍南县期中)如图,AB是⊙O的直径,点C为半径OA的上的中点,CD⊥AB交⊙O于点D和点E,DF∥AB交⊙O于F,连结AF,AD. (1)求∠DAF的度数; (2)若AB=10,求弦AD,AF和所围成的图形的面积.(结果保留π) 23.(2018秋 下城区期中)(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为劣弧BC上一动点.求证:PA=PB+PC; (2)已知:如图2,四边形ABCD是⊙O的内接正方形,点P为劣弧BC上一动点.求证:PA=PC+PB.
学生姓名: 年 级:九年级 科目:数学 学科教师:
课题 圆的有关计算
授课类型 基础知识 典型例题 巩固提升
教学目标 会计算弧长,能计算扇形的面积; 掌握正多边形的有关概念,会计算正多边形的外接圆、内接圆半径。
教学重难点 灵活应用弧长公式、扇形面积公式; 会计算正多边形的外接圆、内接圆半径。
授课日期及时段
教学内容
知识点一 弧长的计算 在半径为R的圆中,n°的圆心角所对的弧长l的计算公式为:l=. 【典例1】(2019秋 鹿城区校级月考)如图,在4×4的正方形网格中,若将△ABC绕着点A逆时针旋转得到△AB′C′,则的长为( ) A.π B. C.7 D.6 【变式训练】 1.(2019秋 庆云县期中)已知圆的半径为3,扇形的圆心角为120°,则扇形的弧长为( ) A.π B.2π C.3π D.4 2.(2019春 萧山区月考)如果一个扇形的半径是3,弧长是π,那么此扇形的圆心角的大小为( ) A.30° B.45° C.60° D.90° 3.(2019 温州模拟)已知圆弧的度数为120°,弧长为12πcm,则圆的半径为( ) A.2 B.6 C.8 D.18 知识点二 与扇形有关的面积计算 在半径为R的圆中,n°的圆心角所对的扇形(弧长为l)面积的计算公式为:S扇形==lR. 【典例2】(2019 温岭市一模)如图,扇形AOB中,OA=2,C为上的一点,连接AC,BC,如果四边形AOBC为菱形,则图中阴影部分的面积为( ) A.﹣ B.﹣2 C.﹣ D.﹣2 【变式训练】 1.(2018秋 象山县期末)已知圆的半径为3,扇形的圆心角为120°,则扇形的面积为( ) A.π B.2π C.3π D.4π 2.(2018秋 吴兴区期末)已知圆心角为60°的扇形面积为24π,那么扇形的半径为( ) A.12 B.6 C.4π D.2π 3.(2018秋 慈溪市期末)如图,在△ABC中,AC=BC=,∠ACB=90°,分别以点A和点B为圆心,以AC的长为半径画弧交AB于D,E两点,则阴影部分的面积是( ) A.﹣1 B.π﹣2 C.2﹣ D.π﹣1 4.(2019 滨江区一模)今年寒假期间,小芮参观了中国扇博物馆,如图是她看到的折扇和团扇.已知折扇的骨柄长为30cm,扇面的宽度为18cm,某扇张开的角度为120°,若这两把扇子的扇面面积相等,则团扇的半径为( )cm. A.6 B.8 C.6 D.8 知识点三 正多边形的相关计算 1.正多边形的中心:正多边形的外接圆的圆心.外接圆的半径叫做正多边形的半径,正多边形每一边所对的圆心角叫做正多边形的中心角,中心到正多边形的一边的距离叫做正多边形的边心距.作相等的圆心角就可以等分圆周,从而得到相应正多边形. 2.每个正多边形都有一个外接圆和一个内切圆,正多边形的边心距就是内切圆的半径.研究正多边形往往构造等腰三角形,并结合勾股定理、三角函数等解决. 【典例3】(2018秋 萧山区期末)边长为2的正方形内接于⊙O,则⊙O的半径是( ) A.1 B. C.2 D.2 【变式训练】 1.如图,已知正五边形ABCDE内接于⊙O,连结BD,则∠ABD的度数是( ) A.60° B.70° C.72° D.144° 2.如图,⊙O是正六边形ABCDEF的外接圆,P是弧EF上一点,则∠BPD的度数是( ) A.30° B.60° C.55° D.75° (2019秋 慈溪市期中)已知⊙O的半径为1,则其内接正六边形的边长为 . 4.(2019 海宁市一模)如图,已知点O是正六边形ABCDEF的对称中心,G,H分别是AF,BC上的点,且AG=BH. (1)求∠FAB的度数; (2)求证:OG=OH. 课堂训练 (2019秋 萧山区期中)正方形ABCD是半径为10的圆内接正方形,则正方形的周长为 . 2.(2019 温州一模)已知一扇形的半径长是4,圆心角为60°,则这个扇形的面积为 . 3.(2019秋 镇海区校级期中)半径为9的圆中,120度的圆心角所对的弧长是( ) A.4π B.5π C.6π D.8π 4.(2018秋 温岭市期末)在⊙O中,60°的圆心角所对的弧长是3π,则⊙O的半径是( ) A.9 B.18 C.9π D.18π 5.(2019秋 江干区校级月考)如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为 (计算结果保留π) 6.(2019秋 瑞安市期中)如图,在边长为2的正方形ABCD中,点E是边CD的中点,以A为圆心,AB为半径作弧,交BE于点F.记图中分割部分的面积为S1,S2,则S1﹣S2的值为( ) A.4﹣π B.2π﹣4 C.6﹣2π D.π﹣3 7.(2018秋 吴兴区期末)如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC. (1)求证:AE=ED; (2)若AB=8,∠CBD=30°,求图中阴影部分的面积. 8.(2018 温州校级月考)如图,在⊙O中,弦AB=弦CD,AB⊥CD于点E,且AE<EB,CE<ED,连结AO,DO,BD. (1)求证:EB=ED. (2)若AO=6,求的长. 一、选择题 1.(2019 温州)若扇形的圆心角为90°,半径为6,则该扇形的弧长为( ) A.π B.2π C.3π D.6π 2.(2019秋 慈溪市期中)钟面上的分针的长为1,从9点到9点15分,分针在钟面上扫过的面积是( ) A.π B.π C. D.π 3.(2018秋 杭州期末)已知圆心角为120°的扇形的弧长为6π,该扇形的面积为( ) A.18π B.27π C.36π D.54π 4.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则劣弧AC的长( ) A.2π B.π C. D.4π 5.(2019秋 萧山区期中)如图,点C是以AB为直径的半圆O的三等分点,AC=2,则图中阴影部分的面积是( ) A. B. C. D. 6.(2019秋 苍南县期中)三个正方形方格在扇形中的位置如图所示,点O为扇形的圆心,格点A,B,C分别在扇形的两条半径和弧上,已知每个方格的边长为1,则的长为( ) A.πcm B. C. D.2πcm 7.(2018秋 吴兴区期末)如图,探究:用6个小正方形构造如图所示的网格图(每个小正方形的边长均为2),设经过图中M、P、H三点的圆弧与AH交于R,则弧HR的弧长为( ) A. B.π C.π D.π 8.(2018秋 黄岩区期末)如图,圆P的半径为10,A、B是圆上任意两点,且AB=12,以AB为边作正方形ABCD(点D、P在直线AB的两侧),若AB边绕点P旋转一周,则CD边扫过的面积为( ) A.0 B.36π C. D.6π 9.(2018秋 椒江区期末)如图,在半径为6cm的⊙O中,点A是劣弧的中点,点D是优弧上一点,且∠D=30°,下列四个结论:①OA⊥BC;②BC=3cm;③扇形OCAB的面积为12π;④四边形ABOC是菱形.其中正确结论的序号是( ) ①③ B.①②③④ C.②③④ D.①③④ 10.(2019 乐清市模拟)如图,半径为3的扇形AOB,∠AOB=120°,以AB为边作矩形ABCD交弧AB于点E,F,且点E,F为弧AB的四等分点,矩形ABCD与弧AB形成如图所示的三个阴影区域,其面积分别为S1,S2,S3,则S1+S3﹣S2为( )(π取3) A. B.+ C.﹣ D. 二、填空题 11.(2019 鹿城区校级一模)如图,已知扇形的圆心角∠AOB=120°,半径OA=2,则扇形的弧长为 _______. 12.(2019秋 鹿城区校级月考)扇形的圆心角是30°.它的半径是6,则扇形的面积是 (结果保留π). 13.(2019秋 秀洲区期中)已知扇形的圆心角为120°,面积为27πcm2,则该扇形所在圆的半径为 . 14.(2018秋 慈溪市期末)如图,A,B,C是⊙O上三点,若∠ABC=120°,⊙O的半径为2,则劣弧AC的长为 . 15.(2018 椒江区模拟)如图,有一个正六边形图片,每组平行的对边距离为3米,点A是正六边形的一个顶点,现点A与数轴的原点O重合,工人将图片沿数轴正方向滚动一周,点A恰好落在数轴点A′上,则点A′对应的实数是 . 16.(2018 路桥区一模)如图,在圆内画正六边形、正五边形,则∠ABC= . 17.(2018秋 滨江区期末)如图,⊙O的半径为6,MN为直径,AB,CD为弦,且AB∥MN∥CD,与的度数和为150°,则图中两块阴影部分面积和为 . 三、解答题 18.(2019 上城区一模)如图,在△ABC中,AB=AC,以边BC为直径的⊙O与边AB交于点D,与边AC交于点E,连结OD,OE. (1)求证:BD=CE. (2)若∠C=55°,BC=10,求扇形DOE的面积. 19.(2018秋 柯桥区期末)如图,在△ABC中,AB=AC,以AB为直径的圆,交AC于E点,交BC于D点. (1)若AB=8,∠C=60°,求阴影部分的面积; (2)当∠A为锐角时,试说明∠A与∠CBE的关系. 20.(2019秋 瑞安市期中)如图,在⊙O中,弦AB⊥弦CD于点E,弦AG⊥弦BC于点F,AG与CD相交于点M. (1)求证:=; (2)若弧=80°,⊙O的半径为6,求+的弧长和. 21.(2019秋 宁海县期中)如图,已知AB是⊙O的直径,C、D是⊙O上的点,OC∥BD,交AD于点E,连结BC. (1)求证:AE=ED; (2)若AB=10,∠CBD=36°,求弧AC的长及扇形AOC的面积. 22.(2019秋 苍南县期中)如图,AB是⊙O的直径,点C为半径OA的上的中点,CD⊥AB交⊙O于点D和点E,DF∥AB交⊙O于F,连结AF,AD. (1)求∠DAF的度数; (2)若AB=10,求弦AD,AF和所围成的图形的面积.(结果保留π) 23.(2018秋 下城区期中)(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为劣弧BC上一动点.求证:PA=PB+PC; (2)已知:如图2,四边形ABCD是⊙O的内接正方形,点P为劣弧BC上一动点.求证:PA=PC+PB.
同课章节目录
