第3章 圆的基本性质 单元检测卷(含解析)
文档属性
| 名称 | 第3章 圆的基本性质 单元检测卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 810.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 10:18:11 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版2022年九年级上册第3章 圆的基本性质 单元检测卷
一.选择题(共10小题,满分30分,每小题3分)
1.已知⊙O的半径长7cm,P为线段OA的中点,若点P在⊙O上,则OA的长是( )
A.等于7cm B.等于14cm C.小于7cm D.大于14cm
2.如图,C是圆O劣弧AB上一点,∠ACB=130°,则∠AOB的度数是( )
A.100° B.110° C.120° D.130°
3.下列说法中正确的是( )
A.平分弦的直径垂直于弦
B.三角形的外心到三角形各定点的距离相等
C.同圆中等弦所对的圆周角相等
D.圆是轴对称图形,对称轴是圆的直径
4.如图,在正方形网格中,线段AB绕点O旋转一定的角度后与线段CD重合(C、D均为格点,A的对应点是点C),若点A的坐标为(﹣1,5),点B的坐标为(3,3),则旋转中心O点的坐标为( )
A.(1,1) B.(4,4)
C.(2,1) D.(1,1)或(4,4)
5.在⊙O中,弦AB等于圆的半径,则它所对应的圆心角的度数为( )
A.120° B.75° C.60° D.30°
6.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=AP=8,则⊙O的半径为( )
A.10 B.8 C.5 D.3
7.如图,四边形ABCD内接于⊙O,DE是⊙O的直径,连接BD.若∠BCD=2∠BAD,则∠BDE的度数是( )
A.25° B.30° C.32.5° D.35°
8.如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则的长为( )
A.6π B.2π C.π D.π
9.如图,已知正六边形P1P2P3P4P5P6边长为2,在正六边形的边上距离P1最远的点到P1的距离为( )
A.3 B.4 C. D.2
10.如图,边长为4的正方形ABCD内接于⊙O,点E是上的一动点(不与A,B重合),点F是上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:①AE=BF;②△OGH是等腰三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△GBH周长的最小值为4+.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共5小题,满分20分,每小题4分)
11.如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=68°,那么∠BOD= .
12.已知一个扇形的半径为2cm,弧长是,则它的面积为 cm2.
13.如图,在⊙O中、三条劣弧AB、BC、CD的长都相等,弦AC与BD相交于点E,弦BA与CD的延长线相交于点F,且∠F=40°,则∠AED的度数为 .
14.如图,正方形ABCD的边长是4,F点是BC边的中点,点H是CD边上的一个动点,以CH为直径作⊙O,连接HF交⊙O于E点,连接DE,则线段DE的最小值为 .
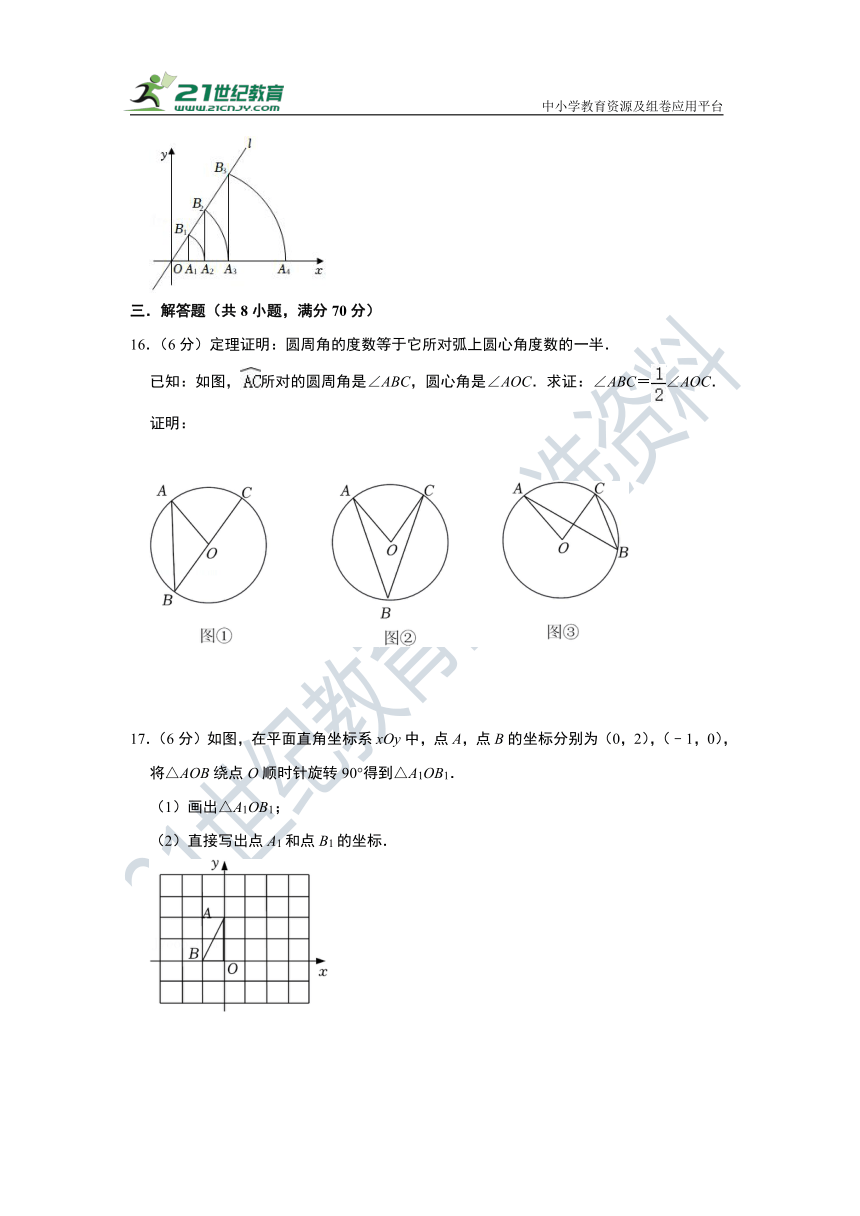
15.如图,直线l为y=x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;…,按此作法进行下去,则点A2022的坐标为 .
三.解答题(共8小题,满分70分)
16.(6分)定理证明:圆周角的度数等于它所对弧上圆心角度数的一半.
已知:如图,所对的圆周角是∠ABC,圆心角是∠AOC.求证:∠ABC=∠AOC.
证明:
17.(6分)如图,在平面直角坐标系xOy中,点A,点B的坐标分别为(0,2),(﹣1,0),将△AOB绕点O顺时针旋转90°得到△A1OB1.
(1)画出△A1OB1;
(2)直接写出点A1和点B1的坐标.
18.(8分)如图所示,某地有一座圆弧形的拱桥,桥下的水面宽度AB为7.2m,拱顶高出水面(CD)2.4m,现有一艘宽EF为3m且船舱顶部为长方形并高出水面1.5m的货船要经过这里,则货船能顺利通过这座拱桥吗?请作出判断并说明理由.
19.(8分)如图,AB是⊙O的直径,CD是弦.
(1)若∠BCD=32°,求∠ABD的度数.
(2)若∠BCD=30°,⊙O的半径r=4,求BD的长.
20.(9分)如图1,在⊙O中,AC=BD,且AC⊥BD,垂足为点E.
(1)求∠ABD的度数;
(2)如图2,连接OA,当OA=2,∠OAB=20°,求的长.
21.(9分)如图,四边形ABCD是⊙O的内接四边形,点F是CD延长线上的一点,且AD平分∠BDF,AE⊥CD于点E.
(1)求证:AB=AC.
(2)若BD=18,DE=2,求CD的长.
22.(12分)如图,四边形ABCD是正方形,点E在AB的延长线上,连接EC,EC绕点E逆时针旋转90°得到EF,连接CF、AF,CF与对角线BD交于点G.
(1)若BE=2,求AF的长度;
(2)求证:AF+2BG=AD.
23.(12分)如图,△ABC内接于⊙O,AE⊥BC于点E,BD⊥AC于点D,延长BD交⊙O于点G,连接AG.
(1)求证:AF=AG;
(2)连接DE,若DE=,∠FAG=105°,求⊙O的半径.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:根据点和圆的位置关系,得OP=7cm,
再根据线段的中点的概念,得OA=2OP=14cm.
故选:B.
2.【解答】解:作劣弧AB所对的圆周角∠ACB,如图,
根据圆内接四边形的性质得∠APB=180°﹣∠ACB=180°﹣130°=50°,
∴∠AOB=2∠APB=100°.
故选:A.
3.【解答】解:A、平分弦(表示直径)的直径垂直于弦,故不符合题意;
B、三角形的外心到三角形各顶点的距离相等,故不符合题意;
C、同圆中等弦所对的圆周角相等,故符合题意;
D、圆是轴对称图形,对称轴是圆的直径所在的直线,故不符合题意;
故选:C.
4.【解答】解:作AC、BD的垂直平分线交于点E,
点E即为旋转中心,E(1,1),
故选:A.
5.【解答】解:连接OA、OB,如图,
∵OA=OB=AB,
∴△OAB为等边三角形,
∴∠AOB=60°,
即弦AB所对应的圆心角的度数为60°.
故选:C.
6.【解答】解:连接OC,
∵AB⊥CD,AB过圆心O,CD=8,
∴CP=DP=4,
设⊙O的半径为R,
∵AP=8,
∴OP=8﹣R,
在Rt△COP中,由勾股定理得:CP2+OP2=OC2,
即(8﹣R)2+42=R2,
解得:R=5,
∴⊙O的半径为5,
故选:C.
7.【解答】解:连接BE,
∵四边形ABCD内接于⊙O,
∴∠BCD+∠BAD=180°,
∵∠BCD=2∠BAD,
∴∠BAD=60°,
由圆周角定理得:∠BED=∠BAD=60°,
∵DE是⊙O的直径,
∴∠EBD=90°,
∴∠BDE=90°﹣60°=30°,
故选:B.
8.【解答】解:∵直径AB=6,
∴半径OB=3,
∵圆周角∠A=30°,
∴圆心角∠BOC=2∠A=60°,
∴的长是=π,
故选:D.
9.【解答】解:如图,连接P1P4,P2P5交于点O.
在正六边形的边上距离P1最远的点是P4,
∵△OP1P2,△OP4P5都是等边三角形,
∴OP1=OP2=P1P1=2,
∴P1P2=4,
故选:B.
10.【解答】解:如图,
∵∠AOB=∠EOF=90°,
∴∠AOE=∠BOF,
∴=,
∴AE=BF,
故①正确,
∵∠EOF+∠ABC=180°,
∴点O、G、B、H共圆,
∴∠OHG=∠ABO=45°,∠OGH=∠CBO=45°,
∴OG=OH,
故②正确;
∵OA=OB,OG=OH,∠AOG=∠BOH,
∴△AOG≌△BOH(SAS),
∴四边形OGBH的面积等于三角形AOB的面积,
故③错误,
∵△GOH是等腰直角三角形,
∴当OG最小时,△GOH的周长最小,
∴当OH⊥BC时,周长最小是:2OK+OK=4+2,
故④错误,
故选:B.
二.填空题(共5小题,满分20分,每小题4分)
11.【解答】解:∵∠A+∠BCD=180°,∠DCE+∠BCD=180°,
∴∠A=∠DCE=68°,
∴∠BOD=2∠A=136°.
故答案为:136°.
12.【解答】解:扇形的面积=××2=(cm2).
故答案为:.
13.【解答】解:连接BC,
∵弧AB、BC、CD的长相等,
∴∠BAC=∠BDC=∠BCA=∠DBC,
设∠ACD=∠ABD=x,
∵∠F=40°,
∴∠BAC=x+40°,
∴∠BDC=∠BCA=∠DBC=x+40°,
在△ABC中,x+40°+x+x+x+40°+40°=180°,
解得x=15°,
∴∠DBC=∠BCA=55°,
∴∠AED=∠BEC=70°.
故答案为:70°.
14.【解答】解:连接CE,
∵CH是⊙O的直径,
∴∠CEH=90°,
∴∠CEF=180°﹣90°=90°,
∴点E在以CF为直径的⊙M上,
连接EM、DM,
∵正方形ABCD的边长是4,F点是BC边的中点,
∴BC=CD=4,∠BCD=90°,CF=BC=2,
∴FM=MC=EM=1,
在Rt△DMC中,DM===,
∵DE≥DM﹣EM,
∴当且仅当D、E、M三点共线时,线段DE取得最小值,
∴线段DE的最小值为﹣1,
故答案为:﹣1.
15.【解答】解:∵A1(1,0)作A1B1⊥x轴,与直线y=x交于点B1,
∴OA1=1,B1(1,1),
∵以原点O为圆心,OB1长为半径画圆弧交x轴于点A2,
∴OA2=OB1=OA1=,
∵以原点O为圆心,OB2长为半径画圆弧交x轴于点A3,
∴OA3=OB2=OA2=×=()2,
同理可得OA4=()3,
∴OA2022=()2021,
∴点A2022的坐标为(()2021,0).
故答案为:(()2021,0).
三.解答题(共8小题,满分70分)
16.【解答】证明:在图①中,
∵OA=OB,
∴∠A=∠B,
又∵∠AOC=∠A+∠B,
∴∠ABC=∠AOC;
在图②中,作直径BD,
同①可得∠ABD=∠AOD,∠CBD=∠COD,
∴∠ABD+∠CBD=(∠AOD+∠COD),
则∠ABC=∠AOC;
在图③中,作直径BD.
同理∠CBD=∠COD,∠ABD=∠AOD,
∴∠ABC=∠CBD﹣∠ABD=∠COD﹣∠AOD=(∠COD﹣∠AOD)=∠AOC.
17.【解答】解:(1)如图,△A1OB1即为所求.
(2)由图可得,点A1的坐标为(2,0),点B1的坐标为(0,1).
18.【解答】解:货船能顺利通过这座拱桥,理由如下:
如图,连接ON、OA.
∵OC⊥AB,AB=7.2m,
∴AD=AB=3.6(m),
设OB=OC=ON=rm,则OD=(r﹣2.4)m,
在Rt△AOD中,根据勾股定理得:r2=(r﹣2.4)2+3.62,
解得:r=3.9.
∵CD=2.4m,船舱顶部为正方形并高出水面1.5m,
∴CH=2.4﹣1.5=0.9(m),
∴OH=3.9﹣0.9=3(m),
在Rt△OHN中,HN2=ON2﹣OH2=3.92﹣32=6.21(m2),
∴HN=(m),
∴MN=2HN=2(m)>3m,
∴货船能顺利通过这座拱桥.
19.【解答】解:(1)∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠BAD=∠BCD=32°,
∴∠ABD=90°﹣∠BAD=90°﹣32°=58°;
(2)∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠BAD=∠BCD=30°,r=4,
∴BD=AB=4.
20.【解答】解:(1)如图1,∵AC=BD,
∴=,
∴=,
∴∠A=∠B,
∵AC⊥BD,
∴∠∠AEB=90°
∴∠ABD=45°;
(2)如图2,连接OB、OC、OD,
∵OA=OB,∠OAB=20°,
∴∠AOB=180°﹣20°﹣20°=140°,
∵∠ABD=∠BAC=45°,
∴∠AOD=∠BOC=45°×2=90°,
∴∠COD=360°﹣140°﹣90°﹣90°=40°,
∴的长=.
21.【解答】(1)证明:∵AD平分∠BDF,
∴∠ADF=∠ADB,
∵∠ABC+∠ADC=180°,∠ADC+∠ADF=180°,
∴∠ADF=∠ABC,
∵∠ACB=∠ADB,
∴∠ABC=∠ACB,
∴AB=AC;
(2)解:过点A作AG⊥BD,垂足为点G.
∵AD平分∠BDF,AE⊥CF,AG⊥BD,
∴AG=AE,∠AGB=∠AEC=90°,
在Rt△AED和Rt△AGD中,
,
∴Rt△AED≌Rt△AGD,
∴GD=ED=2,
在Rt△AEC和Rt△AGB中,
,
∴Rt△AEC≌Rt△AGB(HL),
∴BG=CE,
∵BD=18,
∴BG=BD﹣GD=18﹣2=16,
∴CE=BG=16,
∴CD=CE﹣DE=16﹣2=14.
22.【解答】(1)解:连接AC,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠EBC=90°,AC2=AB2+BC2=2BC2,
∴CE2=BE2+BC2,
∵EC绕点E逆时旋转90°得到EF,
∴EF=EC,∠FEC=90°,
∴∠EFC=∠ECF=45°,CF2=EF2+CE2=2CE2=2BE2+2BC2,
∴∠EFC=∠EAC=45°,
∴∠FAE=∠FCE=45°,
∴∠FAC=90°,
∴CF2=AF2+AC2=AF2+2BC2,
∴AF2+2BC2=2BE2+2BC2,
即AF2=2BE2,
∵BE=2,
∴AF2=2×22=8,
解得AF=;
(2)证明:连接AC,延长AF,CB交于点H,
∵∠FAE=∠ABD=45°,
∴AF∥BD,
又∵AD∥BC,
∴四边形ADBH是平行四边形,
∴AD=BH=BC=AB,
∴AH=AB=CD,
∵AH∥BG,
∴CG=FG,
∴BG是△CBF的中位线,
∴HF=2BG,
∵AH=AF+FH,
∴AD=AF+2BG,
即AF+2BG=AD.
23.【解答】(1)证明:∵AE⊥BC于点E,BD⊥AC于点D,
∴∠ACB+∠EFD=180°,
∵∠AFD+∠EFD=180°,
∴∠AFD=∠ACB,
∵∠AGD=∠ACB,
∴∠AFD=∠AGD,
∴AF=AG;
(2)解:延长AE交⊙O于M,连接BM,GM,GC,MC,MO,作直径GN,作MH⊥GN于H,
∵AF=AG,AC⊥FG,
∴FD=DG,
同理,FE=EM,
∴MG=2DE=2(+),
∵∠MAG+∠MCG=180°,
∴∠MCG=180°﹣∠MAG=180°﹣105°=75°,
∴∠MOG=2∠MCG=150°,
∴∠MOH=30°,
设MH=x,
∴OM=OG=2x,OH=x,
∵MH2+GH2=GM2,
∴x2+(2+)2x2=22(+)2,
∴(8+4)x2=4(8+4),
∴x2=4,
∴x=2,
∴⊙O半径长为2x=4.
浙教版2022年九年级上册第3章 圆的基本性质 单元检测卷
一.选择题(共10小题,满分30分,每小题3分)
1.已知⊙O的半径长7cm,P为线段OA的中点,若点P在⊙O上,则OA的长是( )
A.等于7cm B.等于14cm C.小于7cm D.大于14cm
2.如图,C是圆O劣弧AB上一点,∠ACB=130°,则∠AOB的度数是( )
A.100° B.110° C.120° D.130°
3.下列说法中正确的是( )
A.平分弦的直径垂直于弦
B.三角形的外心到三角形各定点的距离相等
C.同圆中等弦所对的圆周角相等
D.圆是轴对称图形,对称轴是圆的直径
4.如图,在正方形网格中,线段AB绕点O旋转一定的角度后与线段CD重合(C、D均为格点,A的对应点是点C),若点A的坐标为(﹣1,5),点B的坐标为(3,3),则旋转中心O点的坐标为( )
A.(1,1) B.(4,4)
C.(2,1) D.(1,1)或(4,4)
5.在⊙O中,弦AB等于圆的半径,则它所对应的圆心角的度数为( )
A.120° B.75° C.60° D.30°
6.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=AP=8,则⊙O的半径为( )
A.10 B.8 C.5 D.3
7.如图,四边形ABCD内接于⊙O,DE是⊙O的直径,连接BD.若∠BCD=2∠BAD,则∠BDE的度数是( )
A.25° B.30° C.32.5° D.35°
8.如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则的长为( )
A.6π B.2π C.π D.π
9.如图,已知正六边形P1P2P3P4P5P6边长为2,在正六边形的边上距离P1最远的点到P1的距离为( )
A.3 B.4 C. D.2
10.如图,边长为4的正方形ABCD内接于⊙O,点E是上的一动点(不与A,B重合),点F是上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:①AE=BF;②△OGH是等腰三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△GBH周长的最小值为4+.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共5小题,满分20分,每小题4分)
11.如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=68°,那么∠BOD= .
12.已知一个扇形的半径为2cm,弧长是,则它的面积为 cm2.
13.如图,在⊙O中、三条劣弧AB、BC、CD的长都相等,弦AC与BD相交于点E,弦BA与CD的延长线相交于点F,且∠F=40°,则∠AED的度数为 .
14.如图,正方形ABCD的边长是4,F点是BC边的中点,点H是CD边上的一个动点,以CH为直径作⊙O,连接HF交⊙O于E点,连接DE,则线段DE的最小值为 .
15.如图,直线l为y=x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;…,按此作法进行下去,则点A2022的坐标为 .
三.解答题(共8小题,满分70分)
16.(6分)定理证明:圆周角的度数等于它所对弧上圆心角度数的一半.
已知:如图,所对的圆周角是∠ABC,圆心角是∠AOC.求证:∠ABC=∠AOC.
证明:
17.(6分)如图,在平面直角坐标系xOy中,点A,点B的坐标分别为(0,2),(﹣1,0),将△AOB绕点O顺时针旋转90°得到△A1OB1.
(1)画出△A1OB1;
(2)直接写出点A1和点B1的坐标.
18.(8分)如图所示,某地有一座圆弧形的拱桥,桥下的水面宽度AB为7.2m,拱顶高出水面(CD)2.4m,现有一艘宽EF为3m且船舱顶部为长方形并高出水面1.5m的货船要经过这里,则货船能顺利通过这座拱桥吗?请作出判断并说明理由.
19.(8分)如图,AB是⊙O的直径,CD是弦.
(1)若∠BCD=32°,求∠ABD的度数.
(2)若∠BCD=30°,⊙O的半径r=4,求BD的长.
20.(9分)如图1,在⊙O中,AC=BD,且AC⊥BD,垂足为点E.
(1)求∠ABD的度数;
(2)如图2,连接OA,当OA=2,∠OAB=20°,求的长.
21.(9分)如图,四边形ABCD是⊙O的内接四边形,点F是CD延长线上的一点,且AD平分∠BDF,AE⊥CD于点E.
(1)求证:AB=AC.
(2)若BD=18,DE=2,求CD的长.
22.(12分)如图,四边形ABCD是正方形,点E在AB的延长线上,连接EC,EC绕点E逆时针旋转90°得到EF,连接CF、AF,CF与对角线BD交于点G.
(1)若BE=2,求AF的长度;
(2)求证:AF+2BG=AD.
23.(12分)如图,△ABC内接于⊙O,AE⊥BC于点E,BD⊥AC于点D,延长BD交⊙O于点G,连接AG.
(1)求证:AF=AG;
(2)连接DE,若DE=,∠FAG=105°,求⊙O的半径.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:根据点和圆的位置关系,得OP=7cm,
再根据线段的中点的概念,得OA=2OP=14cm.
故选:B.
2.【解答】解:作劣弧AB所对的圆周角∠ACB,如图,
根据圆内接四边形的性质得∠APB=180°﹣∠ACB=180°﹣130°=50°,
∴∠AOB=2∠APB=100°.
故选:A.
3.【解答】解:A、平分弦(表示直径)的直径垂直于弦,故不符合题意;
B、三角形的外心到三角形各顶点的距离相等,故不符合题意;
C、同圆中等弦所对的圆周角相等,故符合题意;
D、圆是轴对称图形,对称轴是圆的直径所在的直线,故不符合题意;
故选:C.
4.【解答】解:作AC、BD的垂直平分线交于点E,
点E即为旋转中心,E(1,1),
故选:A.
5.【解答】解:连接OA、OB,如图,
∵OA=OB=AB,
∴△OAB为等边三角形,
∴∠AOB=60°,
即弦AB所对应的圆心角的度数为60°.
故选:C.
6.【解答】解:连接OC,
∵AB⊥CD,AB过圆心O,CD=8,
∴CP=DP=4,
设⊙O的半径为R,
∵AP=8,
∴OP=8﹣R,
在Rt△COP中,由勾股定理得:CP2+OP2=OC2,
即(8﹣R)2+42=R2,
解得:R=5,
∴⊙O的半径为5,
故选:C.
7.【解答】解:连接BE,
∵四边形ABCD内接于⊙O,
∴∠BCD+∠BAD=180°,
∵∠BCD=2∠BAD,
∴∠BAD=60°,
由圆周角定理得:∠BED=∠BAD=60°,
∵DE是⊙O的直径,
∴∠EBD=90°,
∴∠BDE=90°﹣60°=30°,
故选:B.
8.【解答】解:∵直径AB=6,
∴半径OB=3,
∵圆周角∠A=30°,
∴圆心角∠BOC=2∠A=60°,
∴的长是=π,
故选:D.
9.【解答】解:如图,连接P1P4,P2P5交于点O.
在正六边形的边上距离P1最远的点是P4,
∵△OP1P2,△OP4P5都是等边三角形,
∴OP1=OP2=P1P1=2,
∴P1P2=4,
故选:B.
10.【解答】解:如图,
∵∠AOB=∠EOF=90°,
∴∠AOE=∠BOF,
∴=,
∴AE=BF,
故①正确,
∵∠EOF+∠ABC=180°,
∴点O、G、B、H共圆,
∴∠OHG=∠ABO=45°,∠OGH=∠CBO=45°,
∴OG=OH,
故②正确;
∵OA=OB,OG=OH,∠AOG=∠BOH,
∴△AOG≌△BOH(SAS),
∴四边形OGBH的面积等于三角形AOB的面积,
故③错误,
∵△GOH是等腰直角三角形,
∴当OG最小时,△GOH的周长最小,
∴当OH⊥BC时,周长最小是:2OK+OK=4+2,
故④错误,
故选:B.
二.填空题(共5小题,满分20分,每小题4分)
11.【解答】解:∵∠A+∠BCD=180°,∠DCE+∠BCD=180°,
∴∠A=∠DCE=68°,
∴∠BOD=2∠A=136°.
故答案为:136°.
12.【解答】解:扇形的面积=××2=(cm2).
故答案为:.
13.【解答】解:连接BC,
∵弧AB、BC、CD的长相等,
∴∠BAC=∠BDC=∠BCA=∠DBC,
设∠ACD=∠ABD=x,
∵∠F=40°,
∴∠BAC=x+40°,
∴∠BDC=∠BCA=∠DBC=x+40°,
在△ABC中,x+40°+x+x+x+40°+40°=180°,
解得x=15°,
∴∠DBC=∠BCA=55°,
∴∠AED=∠BEC=70°.
故答案为:70°.
14.【解答】解:连接CE,
∵CH是⊙O的直径,
∴∠CEH=90°,
∴∠CEF=180°﹣90°=90°,
∴点E在以CF为直径的⊙M上,
连接EM、DM,
∵正方形ABCD的边长是4,F点是BC边的中点,
∴BC=CD=4,∠BCD=90°,CF=BC=2,
∴FM=MC=EM=1,
在Rt△DMC中,DM===,
∵DE≥DM﹣EM,
∴当且仅当D、E、M三点共线时,线段DE取得最小值,
∴线段DE的最小值为﹣1,
故答案为:﹣1.
15.【解答】解:∵A1(1,0)作A1B1⊥x轴,与直线y=x交于点B1,
∴OA1=1,B1(1,1),
∵以原点O为圆心,OB1长为半径画圆弧交x轴于点A2,
∴OA2=OB1=OA1=,
∵以原点O为圆心,OB2长为半径画圆弧交x轴于点A3,
∴OA3=OB2=OA2=×=()2,
同理可得OA4=()3,
∴OA2022=()2021,
∴点A2022的坐标为(()2021,0).
故答案为:(()2021,0).
三.解答题(共8小题,满分70分)
16.【解答】证明:在图①中,
∵OA=OB,
∴∠A=∠B,
又∵∠AOC=∠A+∠B,
∴∠ABC=∠AOC;
在图②中,作直径BD,
同①可得∠ABD=∠AOD,∠CBD=∠COD,
∴∠ABD+∠CBD=(∠AOD+∠COD),
则∠ABC=∠AOC;
在图③中,作直径BD.
同理∠CBD=∠COD,∠ABD=∠AOD,
∴∠ABC=∠CBD﹣∠ABD=∠COD﹣∠AOD=(∠COD﹣∠AOD)=∠AOC.
17.【解答】解:(1)如图,△A1OB1即为所求.
(2)由图可得,点A1的坐标为(2,0),点B1的坐标为(0,1).
18.【解答】解:货船能顺利通过这座拱桥,理由如下:
如图,连接ON、OA.
∵OC⊥AB,AB=7.2m,
∴AD=AB=3.6(m),
设OB=OC=ON=rm,则OD=(r﹣2.4)m,
在Rt△AOD中,根据勾股定理得:r2=(r﹣2.4)2+3.62,
解得:r=3.9.
∵CD=2.4m,船舱顶部为正方形并高出水面1.5m,
∴CH=2.4﹣1.5=0.9(m),
∴OH=3.9﹣0.9=3(m),
在Rt△OHN中,HN2=ON2﹣OH2=3.92﹣32=6.21(m2),
∴HN=(m),
∴MN=2HN=2(m)>3m,
∴货船能顺利通过这座拱桥.
19.【解答】解:(1)∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠BAD=∠BCD=32°,
∴∠ABD=90°﹣∠BAD=90°﹣32°=58°;
(2)∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠BAD=∠BCD=30°,r=4,
∴BD=AB=4.
20.【解答】解:(1)如图1,∵AC=BD,
∴=,
∴=,
∴∠A=∠B,
∵AC⊥BD,
∴∠∠AEB=90°
∴∠ABD=45°;
(2)如图2,连接OB、OC、OD,
∵OA=OB,∠OAB=20°,
∴∠AOB=180°﹣20°﹣20°=140°,
∵∠ABD=∠BAC=45°,
∴∠AOD=∠BOC=45°×2=90°,
∴∠COD=360°﹣140°﹣90°﹣90°=40°,
∴的长=.
21.【解答】(1)证明:∵AD平分∠BDF,
∴∠ADF=∠ADB,
∵∠ABC+∠ADC=180°,∠ADC+∠ADF=180°,
∴∠ADF=∠ABC,
∵∠ACB=∠ADB,
∴∠ABC=∠ACB,
∴AB=AC;
(2)解:过点A作AG⊥BD,垂足为点G.
∵AD平分∠BDF,AE⊥CF,AG⊥BD,
∴AG=AE,∠AGB=∠AEC=90°,
在Rt△AED和Rt△AGD中,
,
∴Rt△AED≌Rt△AGD,
∴GD=ED=2,
在Rt△AEC和Rt△AGB中,
,
∴Rt△AEC≌Rt△AGB(HL),
∴BG=CE,
∵BD=18,
∴BG=BD﹣GD=18﹣2=16,
∴CE=BG=16,
∴CD=CE﹣DE=16﹣2=14.
22.【解答】(1)解:连接AC,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠EBC=90°,AC2=AB2+BC2=2BC2,
∴CE2=BE2+BC2,
∵EC绕点E逆时旋转90°得到EF,
∴EF=EC,∠FEC=90°,
∴∠EFC=∠ECF=45°,CF2=EF2+CE2=2CE2=2BE2+2BC2,
∴∠EFC=∠EAC=45°,
∴∠FAE=∠FCE=45°,
∴∠FAC=90°,
∴CF2=AF2+AC2=AF2+2BC2,
∴AF2+2BC2=2BE2+2BC2,
即AF2=2BE2,
∵BE=2,
∴AF2=2×22=8,
解得AF=;
(2)证明:连接AC,延长AF,CB交于点H,
∵∠FAE=∠ABD=45°,
∴AF∥BD,
又∵AD∥BC,
∴四边形ADBH是平行四边形,
∴AD=BH=BC=AB,
∴AH=AB=CD,
∵AH∥BG,
∴CG=FG,
∴BG是△CBF的中位线,
∴HF=2BG,
∵AH=AF+FH,
∴AD=AF+2BG,
即AF+2BG=AD.
23.【解答】(1)证明:∵AE⊥BC于点E,BD⊥AC于点D,
∴∠ACB+∠EFD=180°,
∵∠AFD+∠EFD=180°,
∴∠AFD=∠ACB,
∵∠AGD=∠ACB,
∴∠AFD=∠AGD,
∴AF=AG;
(2)解:延长AE交⊙O于M,连接BM,GM,GC,MC,MO,作直径GN,作MH⊥GN于H,
∵AF=AG,AC⊥FG,
∴FD=DG,
同理,FE=EM,
∴MG=2DE=2(+),
∵∠MAG+∠MCG=180°,
∴∠MCG=180°﹣∠MAG=180°﹣105°=75°,
∴∠MOG=2∠MCG=150°,
∴∠MOH=30°,
设MH=x,
∴OM=OG=2x,OH=x,
∵MH2+GH2=GM2,
∴x2+(2+)2x2=22(+)2,
∴(8+4)x2=4(8+4),
∴x2=4,
∴x=2,
∴⊙O半径长为2x=4.
同课章节目录
