第3章 圆的基本性质 复习课件(28张ppt)
文档属性
| 名称 | 第3章 圆的基本性质 复习课件(28张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 21:03:29 | ||
图片预览




文档简介
(共28张PPT)
第3章 圆的基本性质 复习
浙教版九年级上册
考点梳理
与圆有关
的性质
圆
与圆有关
的位置
与圆有关
的计算
圆与三角形、
四边形综合
隐圆(最值、
轨迹等)
考点梳理
1、圆的有关概念
★注意“弦”与“弧”之间的区别.
1.圆:在同一平面内,线段OP绕它固定的一个端点O旋转
一周,另一端点P所经过的封闭曲线叫做圆,定点O叫做
圆心,线段OP叫做圆的半径.
★圆心确定圆的位置,半径确定圆的大小.
2.弦、直径:连结圆上任意两点的线段叫做弦,
经过圆心的弦叫做直径.
★直经是同圆 中最长的弦,直径等于半径的2倍.
3.弧、半圆:圆上任意两点间的部分叫做圆弧,简称弧,
圆的任意一条直径的两个端点分圆成两条弧,每一条
弧都叫做半圆.
考点梳理
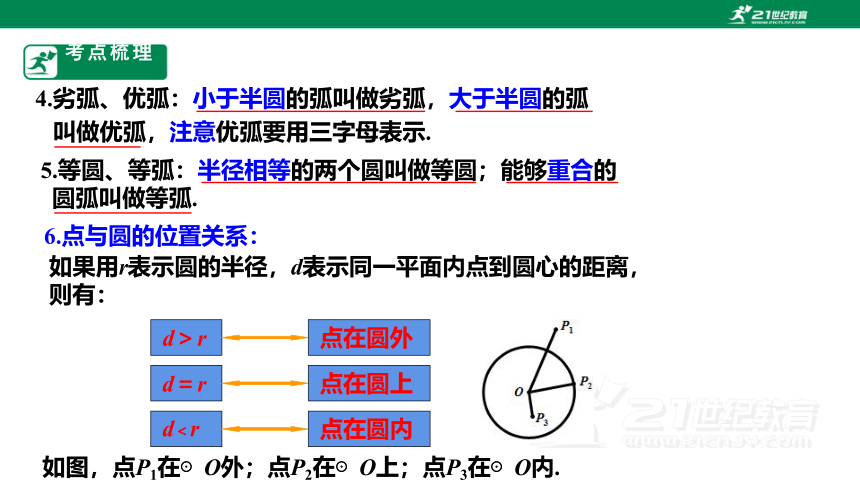
6.点与圆的位置关系:
如果用r表示圆的半径,d表示同一平面内点到圆心的距离,
则有:
d>r
点在圆外
d=r
点在圆上
d<r
点在圆内
如图,点P1在⊙O外;点P2在⊙O上;点P3在⊙O内.
4.劣弧、优弧:小于半圆的弧叫做劣弧,大于半圆的弧
叫做优弧,注意优弧要用三字母表示.
5.等圆、等弧:半径相等的两个圆叫做等圆;能够重合的
圆弧叫做等弧.
考点梳理
8.三角形与圆的位置关系:
(2)三角形的外心是三角形三条边的垂直平分线的交点.
△ABC是⊙O的内接三角形;
如图:
⊙O是△ABC的外接圆;
点O是△ABC的外心.
7.圆的确定:不在同一条直线上的三点确定一个圆.
(1)经过三角形各个顶点的圆叫做三角形的外接圆,这个
外接圆的圆心叫做三角形的外心,三角形叫做圆的内
接三角形.
基础过关
1、在一个圆中任意引圆的两条直径,顺次连接它们的四个端点,组成一个四边形,则这个四边形一定是( )
A.菱形 B.等腰梯形 C.正方形 D.矩形
D
2、如图,在半径为5cm的圆中,圆心O到弦AB的距离为4cm,则弦AB的长为( )
A.4cm B.6cm C.8cm D.10cm
B
基础过关
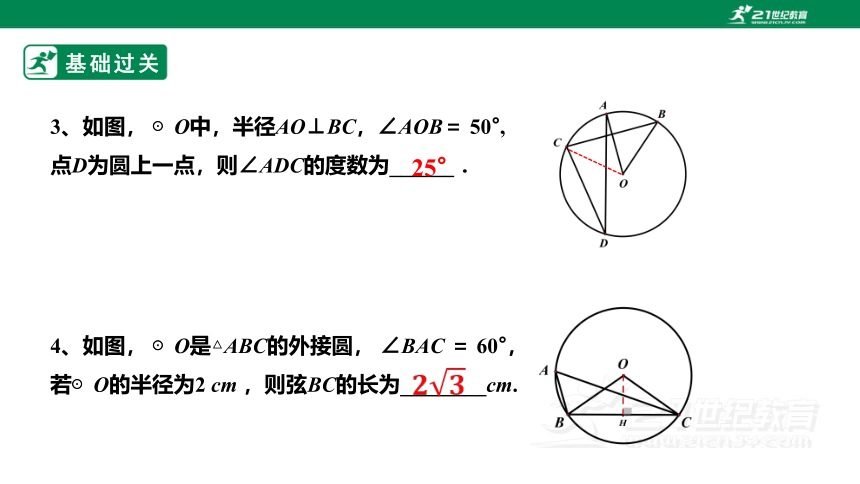
4、如图, ⊙O是△ABC的外接圆, ∠BAC = 60°,
若⊙O的半径为2 cm ,则弦BC的长为________cm.
3、如图, ⊙O中,半径AO⊥BC,∠AOB= 50°,
点D为圆上一点,则∠ADC的度数为______ .
25°
考点梳理
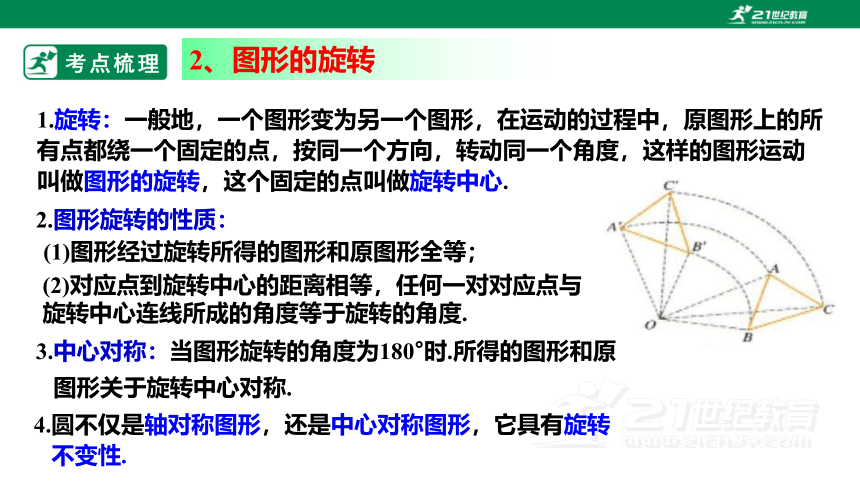
2、图形的旋转
1.旋转:一般地,一个图形变为另一个图形,在运动的过程中,原图形上的所 有点都绕一个固定的点,按同一个方向,转动同一个角度,这样的图形运动叫做图形的旋转,这个固定的点叫做旋转中心.
(1)图形经过旋转所得的图形和原图形全等;
2.图形旋转的性质:
(2)对应点到旋转中心的距离相等,任何一对对应点与旋转中心连线所成的角度等于旋转的角度.
3.中心对称:当图形旋转的角度为180°时.所得的图形和原
图形关于旋转中心对称.
4.圆不仅是轴对称图形,还是中心对称图形,它具有旋转
不变性.
基础过关
5.下列图形中,旋转120°后能与原图形重合的是( )
A.等边三角形 B.正方形 C.正五边形 D.正八边形
A
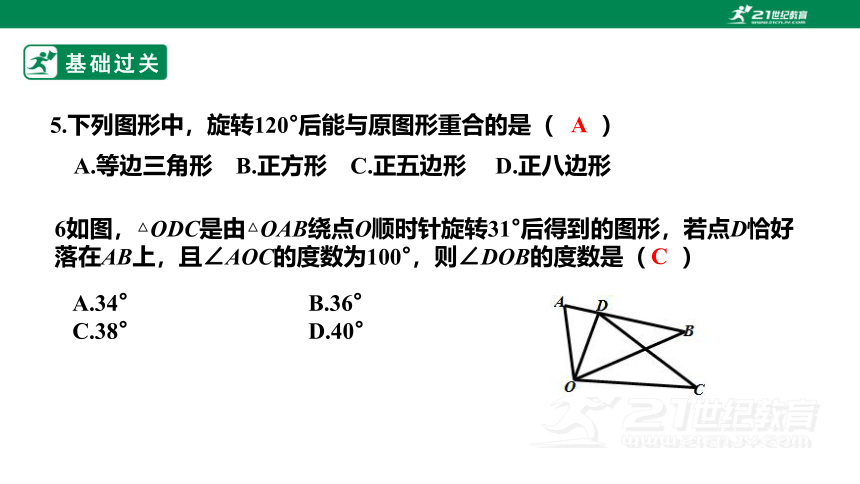
6如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )
A.34° B.36°
C.38° D.40°
C
基础过关
7.下列说法中错误的是( )
A.成中心对称的两个图形全等
B.成中心对称的两个图形中,对称点的连线被对称轴平分
C.中心对称图形的对称中心是对称点连线的中心
D.中心对称图形绕对称中心旋转180°后,都能与自身重合
B
8.下列图形中既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
A
考点梳理
3、垂径定理
1.垂径定理:垂直于弦的直径平分这条弦所对的弧.
2.推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所
对的弧.
推论2:平分弧的直径垂直平分弧所对的弦.
3.弧的中点:分一条弧成相等的两条弧的点.
4.弦心距:圆心到圆的一条弦的距离.
基础过关
9.如图,已知∠ACD=30°,BD是直径,则 ∠AOB=____
120°
10.已知AB 是直径,C,P,F 是⊙O 上的点,则∠1+∠2=____
转化思想
90°
考点梳理
4、圆心角
1.圆心角:顶点在圆心的角叫做圆心角.
2.圆心角定理:在同圆或等圆中,相等的圆心角所对的弧
相等,所对的弦也相等.
3.推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一对量相等,那么它们所对应的其余各对量都相等.
基础过关
11.在同圆或等圆中,下列说法错误的是( )
C.相等的圆心角所对的弧相等
B.相等的弦所对的圆心角相等
A.相等的弦所对的弧相等
D.相等的圆心角所对的弦相等
A.54° B.60°
C.64° D.68°
12.如图,AB,CD是⊙O的直径, ,
若∠AOE=32°,则∠COE的度数是( )
A
C
考点梳理
5、圆周角
1.圆周角:顶点在圆上,两边都与圆相交的角叫做圆周角.
2.圆周角定理:圆周角的度数等于它
所对弧上的圆心角度数的一半.
3.推论1:半圆(或直径)所对的圆周角是直角;90°的圆
周角所对的弦是直径.
推论2:在同圆或等圆中,同弧或等弧所对的圆周角
相等;相等的圆周角所对的弧也相等.
基础过关
13.下列命题中,正确的命题个数是( )
14.如图,在⊙O中,弦AC∥半径OB,
∠BOC=50°,则∠OAB的度数为( )
A.25° B.50°
C.60° D.30°
A.1个 B.2个 C.3个 D.4个
①顶点在圆周上的角是圆周角;
②圆周角度数等于圆心角度数的一半;
③90°的圆周角所对的弦是直径;
④圆周角相等,则它们所对的弧也相等.
A
A
考点梳理
1.圆内接四边形:如果一个四边形的各个顶点在同一个圆上,那么这个四边形叫做圆的内接四边形,这个圆叫做四边形的外接圆.
2.圆内接四边形的性质定理:圆内接四边形的对角互补.
6、圆内接四边形
四边形ABCD是⊙O的内接四边形
⊙O是四边形ABCD的外接圆
3.推论:圆内接四边形的一个外角等于它的内对角.
∠EAD=∠C
基础过关
15.如图,四边形ABCD内接于⊙O,已知
∠ADC=140°,则∠AOC的大小是( )
A.80° B.100°
C.60° D.40°
16.如图,MN是⊙O的直径,若∠E=25°,
∠PMQ=35°,则∠MQP的度数为( )
A.30° B.35°
C.40° D.50°
A
C
考点梳理
1.正多边形:各边都相等、各内角也相等的多边形.
2.正多边形与圆的位置关系
7、正多边形
经过一个正多边形的各个顶点的圆叫做这个正多边形
的外接圆,这个正多边形叫做圆内接正多边形,任何正
多边形都有一个外接圆.
基础过关
17.顺次连结正六边形的三个不相邻的顶点,得到如图
的图形,下列说法错误的是( )
△ACE是等边三角形
此图既是轴对称图形也是中心对称图形
连结AD,则AD分别平分∠EAC与∠EDC
图中一共能画出3条对称轴
18.如图,正六边形ABCDEF内接于⊙O,半径为
4,则这个正六边形的边心距OM和 的长分别为( )
B
D
考点梳理
8、 弧长及扇形的面积
1.弧长计算公式
如果扇形的半径为R,圆心角为n°,扇形的弧长为l,
那么扇形面积S的计算公式为:
2.扇形面积的计算公式
在半径为R的圆中,n°圆心角所对的弧长l的计算公式为:
基础过关
19.如图,四边形ABCD是⊙O的内接四边形,
⊙O的半径为2,∠B=135°则 的长( )
B
20.如图,⊙O的半径为2,AB、CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A、B、C、D不重合),经过P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,点Q走过的路径长为( )
A
基础过关
23.如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD= ,
则阴影部分图形的面积为( )
D
24.如图,等腰直角△ABC中,
AB=AC=8,以AB为直径的半圆O交斜
边BC于D,则阴影部分面积为(结果
保留 )( )
A
典例讲解
1.如图,⊙O 是△ABC的外接圆,弦CD平分∠ACB交⊙O于D,连AD,BD,若直径 AB=10 ,弦 AC=6 .
1
2
(1)你能求出哪些线段的长度?
(2)求 的值.
∠ACB=90°
m
n
思考:若直径 AB=m ,弦 AC=n .
则 的值会发生变化吗?
典例讲解
1.如图,⊙O 是△ABC的外接圆,弦CD平分∠ACB交⊙O于D,连AD,BD,若直径AB=10,弦AC=6.
思考:求 的值.
变1:
若弦AB=m ,弦AC=n,∠ACB=60°.
变2:
若弦AB=m ,弦AC=n ,∠ACB=2α.
1
2
求 的值.
求 的值.
小结提高
与圆有关
的性质
圆
与圆有关
的位置
与圆有关
的计算
圆与三角形、
四边形综合
隐圆(最值、
轨迹等)
……
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第3章 圆的基本性质 复习
浙教版九年级上册
考点梳理
与圆有关
的性质
圆
与圆有关
的位置
与圆有关
的计算
圆与三角形、
四边形综合
隐圆(最值、
轨迹等)
考点梳理
1、圆的有关概念
★注意“弦”与“弧”之间的区别.
1.圆:在同一平面内,线段OP绕它固定的一个端点O旋转
一周,另一端点P所经过的封闭曲线叫做圆,定点O叫做
圆心,线段OP叫做圆的半径.
★圆心确定圆的位置,半径确定圆的大小.
2.弦、直径:连结圆上任意两点的线段叫做弦,
经过圆心的弦叫做直径.
★直经是同圆 中最长的弦,直径等于半径的2倍.
3.弧、半圆:圆上任意两点间的部分叫做圆弧,简称弧,
圆的任意一条直径的两个端点分圆成两条弧,每一条
弧都叫做半圆.
考点梳理
6.点与圆的位置关系:
如果用r表示圆的半径,d表示同一平面内点到圆心的距离,
则有:
d>r
点在圆外
d=r
点在圆上
d<r
点在圆内
如图,点P1在⊙O外;点P2在⊙O上;点P3在⊙O内.
4.劣弧、优弧:小于半圆的弧叫做劣弧,大于半圆的弧
叫做优弧,注意优弧要用三字母表示.
5.等圆、等弧:半径相等的两个圆叫做等圆;能够重合的
圆弧叫做等弧.
考点梳理
8.三角形与圆的位置关系:
(2)三角形的外心是三角形三条边的垂直平分线的交点.
△ABC是⊙O的内接三角形;
如图:
⊙O是△ABC的外接圆;
点O是△ABC的外心.
7.圆的确定:不在同一条直线上的三点确定一个圆.
(1)经过三角形各个顶点的圆叫做三角形的外接圆,这个
外接圆的圆心叫做三角形的外心,三角形叫做圆的内
接三角形.
基础过关
1、在一个圆中任意引圆的两条直径,顺次连接它们的四个端点,组成一个四边形,则这个四边形一定是( )
A.菱形 B.等腰梯形 C.正方形 D.矩形
D
2、如图,在半径为5cm的圆中,圆心O到弦AB的距离为4cm,则弦AB的长为( )
A.4cm B.6cm C.8cm D.10cm
B
基础过关
4、如图, ⊙O是△ABC的外接圆, ∠BAC = 60°,
若⊙O的半径为2 cm ,则弦BC的长为________cm.
3、如图, ⊙O中,半径AO⊥BC,∠AOB= 50°,
点D为圆上一点,则∠ADC的度数为______ .
25°
考点梳理
2、图形的旋转
1.旋转:一般地,一个图形变为另一个图形,在运动的过程中,原图形上的所 有点都绕一个固定的点,按同一个方向,转动同一个角度,这样的图形运动叫做图形的旋转,这个固定的点叫做旋转中心.
(1)图形经过旋转所得的图形和原图形全等;
2.图形旋转的性质:
(2)对应点到旋转中心的距离相等,任何一对对应点与旋转中心连线所成的角度等于旋转的角度.
3.中心对称:当图形旋转的角度为180°时.所得的图形和原
图形关于旋转中心对称.
4.圆不仅是轴对称图形,还是中心对称图形,它具有旋转
不变性.
基础过关
5.下列图形中,旋转120°后能与原图形重合的是( )
A.等边三角形 B.正方形 C.正五边形 D.正八边形
A
6如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )
A.34° B.36°
C.38° D.40°
C
基础过关
7.下列说法中错误的是( )
A.成中心对称的两个图形全等
B.成中心对称的两个图形中,对称点的连线被对称轴平分
C.中心对称图形的对称中心是对称点连线的中心
D.中心对称图形绕对称中心旋转180°后,都能与自身重合
B
8.下列图形中既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
A
考点梳理
3、垂径定理
1.垂径定理:垂直于弦的直径平分这条弦所对的弧.
2.推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所
对的弧.
推论2:平分弧的直径垂直平分弧所对的弦.
3.弧的中点:分一条弧成相等的两条弧的点.
4.弦心距:圆心到圆的一条弦的距离.
基础过关
9.如图,已知∠ACD=30°,BD是直径,则 ∠AOB=____
120°
10.已知AB 是直径,C,P,F 是⊙O 上的点,则∠1+∠2=____
转化思想
90°
考点梳理
4、圆心角
1.圆心角:顶点在圆心的角叫做圆心角.
2.圆心角定理:在同圆或等圆中,相等的圆心角所对的弧
相等,所对的弦也相等.
3.推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一对量相等,那么它们所对应的其余各对量都相等.
基础过关
11.在同圆或等圆中,下列说法错误的是( )
C.相等的圆心角所对的弧相等
B.相等的弦所对的圆心角相等
A.相等的弦所对的弧相等
D.相等的圆心角所对的弦相等
A.54° B.60°
C.64° D.68°
12.如图,AB,CD是⊙O的直径, ,
若∠AOE=32°,则∠COE的度数是( )
A
C
考点梳理
5、圆周角
1.圆周角:顶点在圆上,两边都与圆相交的角叫做圆周角.
2.圆周角定理:圆周角的度数等于它
所对弧上的圆心角度数的一半.
3.推论1:半圆(或直径)所对的圆周角是直角;90°的圆
周角所对的弦是直径.
推论2:在同圆或等圆中,同弧或等弧所对的圆周角
相等;相等的圆周角所对的弧也相等.
基础过关
13.下列命题中,正确的命题个数是( )
14.如图,在⊙O中,弦AC∥半径OB,
∠BOC=50°,则∠OAB的度数为( )
A.25° B.50°
C.60° D.30°
A.1个 B.2个 C.3个 D.4个
①顶点在圆周上的角是圆周角;
②圆周角度数等于圆心角度数的一半;
③90°的圆周角所对的弦是直径;
④圆周角相等,则它们所对的弧也相等.
A
A
考点梳理
1.圆内接四边形:如果一个四边形的各个顶点在同一个圆上,那么这个四边形叫做圆的内接四边形,这个圆叫做四边形的外接圆.
2.圆内接四边形的性质定理:圆内接四边形的对角互补.
6、圆内接四边形
四边形ABCD是⊙O的内接四边形
⊙O是四边形ABCD的外接圆
3.推论:圆内接四边形的一个外角等于它的内对角.
∠EAD=∠C
基础过关
15.如图,四边形ABCD内接于⊙O,已知
∠ADC=140°,则∠AOC的大小是( )
A.80° B.100°
C.60° D.40°
16.如图,MN是⊙O的直径,若∠E=25°,
∠PMQ=35°,则∠MQP的度数为( )
A.30° B.35°
C.40° D.50°
A
C
考点梳理
1.正多边形:各边都相等、各内角也相等的多边形.
2.正多边形与圆的位置关系
7、正多边形
经过一个正多边形的各个顶点的圆叫做这个正多边形
的外接圆,这个正多边形叫做圆内接正多边形,任何正
多边形都有一个外接圆.
基础过关
17.顺次连结正六边形的三个不相邻的顶点,得到如图
的图形,下列说法错误的是( )
△ACE是等边三角形
此图既是轴对称图形也是中心对称图形
连结AD,则AD分别平分∠EAC与∠EDC
图中一共能画出3条对称轴
18.如图,正六边形ABCDEF内接于⊙O,半径为
4,则这个正六边形的边心距OM和 的长分别为( )
B
D
考点梳理
8、 弧长及扇形的面积
1.弧长计算公式
如果扇形的半径为R,圆心角为n°,扇形的弧长为l,
那么扇形面积S的计算公式为:
2.扇形面积的计算公式
在半径为R的圆中,n°圆心角所对的弧长l的计算公式为:
基础过关
19.如图,四边形ABCD是⊙O的内接四边形,
⊙O的半径为2,∠B=135°则 的长( )
B
20.如图,⊙O的半径为2,AB、CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A、B、C、D不重合),经过P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,点Q走过的路径长为( )
A
基础过关
23.如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD= ,
则阴影部分图形的面积为( )
D
24.如图,等腰直角△ABC中,
AB=AC=8,以AB为直径的半圆O交斜
边BC于D,则阴影部分面积为(结果
保留 )( )
A
典例讲解
1.如图,⊙O 是△ABC的外接圆,弦CD平分∠ACB交⊙O于D,连AD,BD,若直径 AB=10 ,弦 AC=6 .
1
2
(1)你能求出哪些线段的长度?
(2)求 的值.
∠ACB=90°
m
n
思考:若直径 AB=m ,弦 AC=n .
则 的值会发生变化吗?
典例讲解
1.如图,⊙O 是△ABC的外接圆,弦CD平分∠ACB交⊙O于D,连AD,BD,若直径AB=10,弦AC=6.
思考:求 的值.
变1:
若弦AB=m ,弦AC=n,∠ACB=60°.
变2:
若弦AB=m ,弦AC=n ,∠ACB=2α.
1
2
求 的值.
求 的值.
小结提高
与圆有关
的性质
圆
与圆有关
的位置
与圆有关
的计算
圆与三角形、
四边形综合
隐圆(最值、
轨迹等)
……
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
