第1-2章 三角形的初步知识+特殊三角形 综合复习-----识别模型,描出模型 课件(19张ppt)
文档属性
| 名称 | 第1-2章 三角形的初步知识+特殊三角形 综合复习-----识别模型,描出模型 课件(19张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 309.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 00:00:00 | ||
图片预览


文档简介
(共19张PPT)
任何几何难题的解决,最终必回到基本图形,基本规律,基本知识
浙教版八上数学
第1-2章 三角形的初步知识+特殊三角形 综合复习
--------------识别模型,描出模型
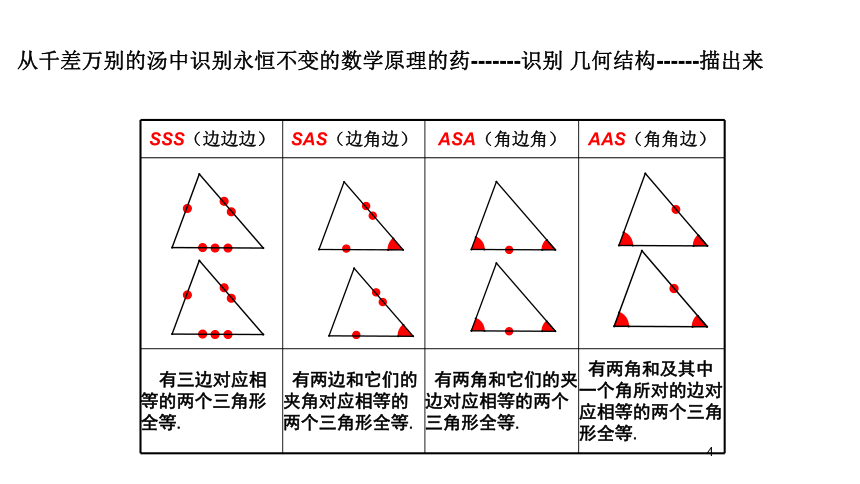
从千差万别的汤中识别永恒不变的数学原理的药-------识别 几何结构------描出来
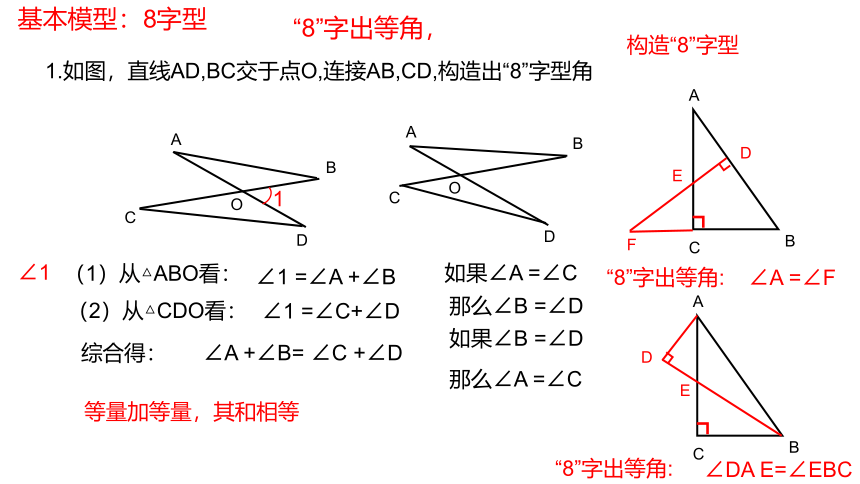
1.如图,直线AD,BC交于点O,连接AB,CD,构造出“8”字型角
“8”字出等角,
O
A
D
B
C
1
(1)从△ABO看:
∠1
∠1 =∠A +∠B
(2)从△CDO看:
∠1 =∠C+∠D
综合得: ∠A +∠B= ∠C +∠D
O
A
D
B
C
如果∠A =∠C
那么∠B =∠D
那么∠A =∠C
如果∠B =∠D
等量加等量,其和相等
A
B
C
┗
┗
D
E
F
“8”字出等角:
∠A =∠F
A
B
C
┗
┛
D
E
“8”字出等角:
∠DA E=∠EBC
基本模型:8字型
构造“8”字型
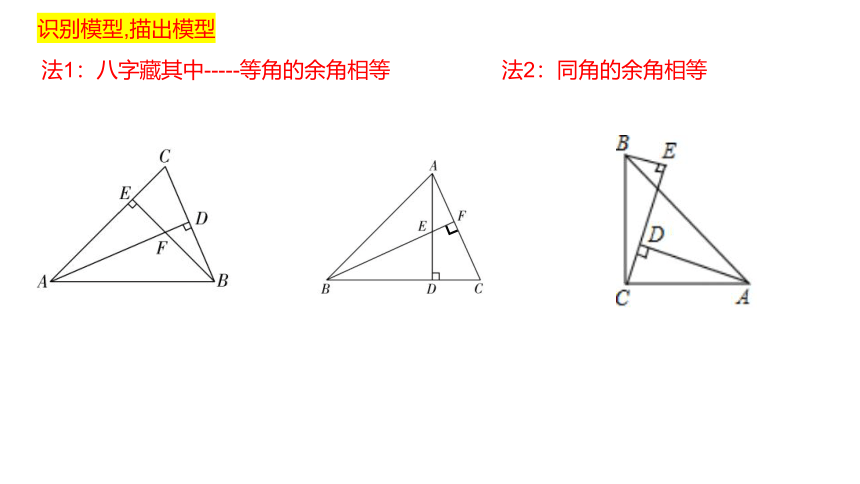
法1:八字藏其中-----等角的余角相等
┓
法2:同角的余角相等
识别模型,描出模型
从千差万别的汤中识别永恒不变的数学原理的药-------识别几何结构------描出来SSS(边边边)SAS(边角边)ASA(角边角)AAS(角角边)有三边对应相等的两个三角形全等.有两边和它们的夹角对应相等的两个三角形全等.有两角和它们的夹边对应相等的两个三角形全等.有两角和及其中一个角所对的边对应相等的两个三角形全等.文字语言:
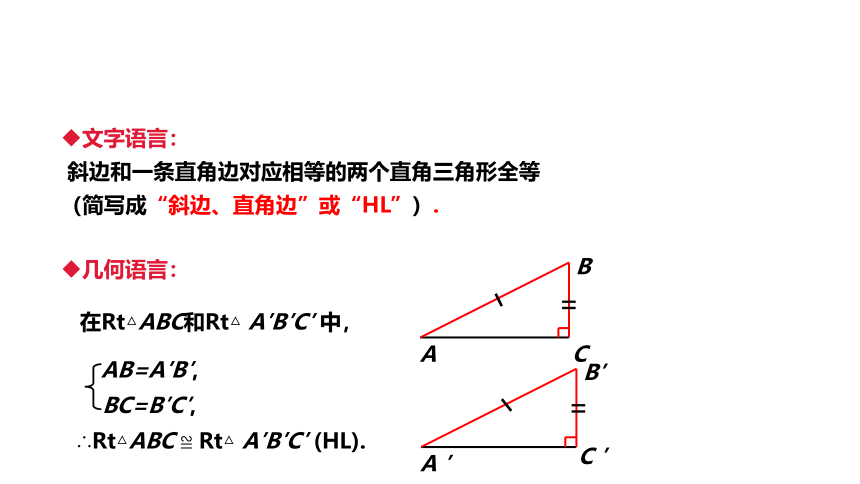
斜边和一条直角边对应相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”).
几何语言:
在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
AB=A′B′,
BC=B′C′,
A
B
C
A ′
B′
C ′
=
=
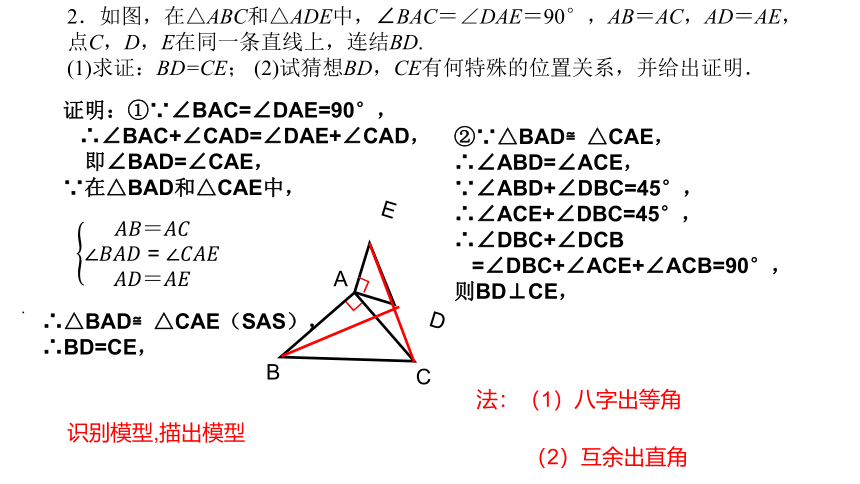
2.如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,
点C,D,E在同一条直线上,连结BD.
(1)求证:BD=CE; (2)试猜想BD,CE有何特殊的位置关系,并给出证明.
D
E
A
B
C
证明:①∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
∵在△BAD和△CAE中,
②∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵∠ABD+∠DBC=45°,
∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB
=∠DBC+∠ACE+∠ACB=90°,
则BD⊥CE,
.
∴△BAD≌△CAE(SAS),∴BD=CE,
法:(1)八字出等角
(2)互余出直角
识别模型,描出模型
3:如图,△BEF的一个顶点E落在△ABD的边AD上,AB与 EF相交于点P. 若∠1=∠2=∠3,AB=BF,求证:AD=EF.
证明:∠1=∠3
.
∠F=1800-∠1-∠BPF
∠A=1800-∠3-∠APE
∠BPF=∠APE
.
八字藏其中
∠1=∠2
.
.
即:∠FBE=∠ABD
等量加等量,其和相等
.
(ASA)
≌
.
D
B
2
A
E
F
P
1
3
识别模型,描出模型
A
C
D
E
B
∠CBA+ ∠DBA = ∠EBD+ ∠DBA=1200
∠CBA= ∠EBD= 60°
CB= AB
DB = EB
∠CBD= ∠ABE
4、如图,已知:点C、B、E在同一条直线上,ΔABC和ΔBDE是等边三角形。求证: ∠EAB= ∠DCB
∠EAB= ∠DCB
ΔCBD ≌ ΔABE
识别模型,描出模型
问题:再找一个600
八字出等角
A
C
D
E
B
G
H
变式1: 如图,已知△ABC和△DEB等边三角形 。
C,B,E在一条直线上。 求证: BG = BH。
识别全等,描出全等:
法1:ΔEBG ≌ ΔDBH(ASA)
法2:ΔBGA ≌ ΔBHC(ASA)
D
E
变式2:如图,△ABC和△CDE都是等边三角形,
A
B
C
识别模型,描出模型
5.如图,在 △ABC中,∠BAC=90°,AB=AC,∠ABC的平分线交AC于点D,过点C作BD的垂线交BD的延长线于点E,交BA的延长线于点F.求证:BD=2CE.
3个基本模型: (1) 8字型------∠ABD=∠ECD
(2) 二线合一-----等腰三角形------三线合一-----CF=2CE
(3)全等模型---------ΔABD ≌ ΔACF(ASA)---------BD=CF
任何几何难题的解决,最终必回到基本图形,基本规律,基本知识
识别模型,描出模型
6.将两个全等的直角三角形按如图所示叠放,AD与BC交于点E. 若AC=6,BC=10,求BE的长.
A
B
C
D
E
识别模型,描出模型:
全等模型:ΔABC≌ ΔBAD
∠1=∠2
1
2
BD=AC=6
AE=BE
AD=BC=10
AD-AE=BC-BE,即CE=ED= x
x
10-x
6
x
10-x
6
x2+62=(10-x)2
x=3.2
BE=10-3.2=6.8
等腰三角形模型
直角三角形模型
7.如图,D、E分别是等边三角形ABC的两边AB、AC上的点,且AD=CE,BE,DC相交于点P,求∠BPD的度数
从千差万别的汤中识别永恒不变的数学原理的药
全等藏其中
ΔACD≌ ΔCBE (SAS)
ΔBCD≌ ΔABE (SAS)
∠BPD=x+(60-x)=600
X
X
60-X
全等出等角、等边
描出基本图形,并写出相应的结论
8.如图,△ABC中,∠ABC,∠ACB的平分线相交于O,MN过点O且与BC平行,△ABC的周长为20,△AMN的周长为12,求BC的长
角平分线+平行=等腰三角形
BM=OM
CN=ON
C△AMN=AM+MN+AN=(AM+BM)+(CN+AN)=AB+BC=12
MN=OM+ON=BM+CN
BC=C△ABC - (AB+BC)=C△AMN - C△ABC=20-12=8
BC的长-----周长差
描出基本图形,并写出相应的结论
9.如图,在锐角三角形ABC中,AB=4,△ABC的面积为10,BD平分 ∠ABC,若M、N分别是BD、BC上的动点,求CM+MN的最小值
基本模型:将军饮马+斜大于直
┗
F
AB边上的高线CF就是CM+MN的最小值
N
'
CM+MN最小值=CF=10×2÷4=5
画出最小值
10.如图,E是等边三角形ABC中AC边上的点,∠1=∠2,BE=CD,则△ADE的形状是( )
A.一般等腰三角形 B.等边三角形
C.不等边三角形 D.不能确定形状
【解】 ∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°.
又∵∠1=∠2,BE=CD, ∴△ABE≌△ACD(SAS)..
∴AE=AD,∠CAD=∠BAE=60°.
∴△ADE是等边三角形.
B
关键点-------描出全等三角形
11. 如图,在△ABC中,AC=5,AB=7,AD平分∠BAC,DE⊥AC,DE=2,求△ABC的面积
角平分线模型-------图中有角平分线,可向两边作垂线
┗
F
DF=DE=2
S△ABC=S△ABD+S△ACD
=5+7=12
=
.
12.如图,CD是等腰三角形 △ABC底边上的中线,BE平分∠ABC,交CD于点E,AC=8,DE=2,求△ BCE的面积
┗
F
┗
基本模型:等腰三角形模型 + 角平分线模型
S△BCE=8×2÷2=8
BC=AC=8
EF=DE=2
图中有角平分线,可向两边作垂线
13.如图,△ABC 中,∠BAC=1300 ,AB ,AC 的垂直平分线分别交 BC于点E,F,与 AB ,AC 分别交于点D,G,求∠EAF 的度数
垂直平分线--------等腰三角形
∠B+∠C=1800-∠BAC
=1800-1300=500
AE=BE
AF=CF
∠B=∠EAB
∠C=∠FAG
∠EAB+∠FAG=∠B+∠C=500
∠EAF= ∠BAC - (∠EAB+∠FAG)
=1300-500=800
任何几何难题的解决,最终必回到基本图形,基本规律,基本知识
浙教版八上数学
第1-2章 三角形的初步知识+特殊三角形 综合复习
--------------识别模型,描出模型
从千差万别的汤中识别永恒不变的数学原理的药-------识别 几何结构------描出来
1.如图,直线AD,BC交于点O,连接AB,CD,构造出“8”字型角
“8”字出等角,
O
A
D
B
C
1
(1)从△ABO看:
∠1
∠1 =∠A +∠B
(2)从△CDO看:
∠1 =∠C+∠D
综合得: ∠A +∠B= ∠C +∠D
O
A
D
B
C
如果∠A =∠C
那么∠B =∠D
那么∠A =∠C
如果∠B =∠D
等量加等量,其和相等
A
B
C
┗
┗
D
E
F
“8”字出等角:
∠A =∠F
A
B
C
┗
┛
D
E
“8”字出等角:
∠DA E=∠EBC
基本模型:8字型
构造“8”字型
法1:八字藏其中-----等角的余角相等
┓
法2:同角的余角相等
识别模型,描出模型
从千差万别的汤中识别永恒不变的数学原理的药-------识别几何结构------描出来SSS(边边边)SAS(边角边)ASA(角边角)AAS(角角边)有三边对应相等的两个三角形全等.有两边和它们的夹角对应相等的两个三角形全等.有两角和它们的夹边对应相等的两个三角形全等.有两角和及其中一个角所对的边对应相等的两个三角形全等.文字语言:
斜边和一条直角边对应相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”).
几何语言:
在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
AB=A′B′,
BC=B′C′,
A
B
C
A ′
B′
C ′
=
=
2.如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,
点C,D,E在同一条直线上,连结BD.
(1)求证:BD=CE; (2)试猜想BD,CE有何特殊的位置关系,并给出证明.
D
E
A
B
C
证明:①∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
∵在△BAD和△CAE中,
②∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵∠ABD+∠DBC=45°,
∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB
=∠DBC+∠ACE+∠ACB=90°,
则BD⊥CE,
.
∴△BAD≌△CAE(SAS),∴BD=CE,
法:(1)八字出等角
(2)互余出直角
识别模型,描出模型
3:如图,△BEF的一个顶点E落在△ABD的边AD上,AB与 EF相交于点P. 若∠1=∠2=∠3,AB=BF,求证:AD=EF.
证明:∠1=∠3
.
∠F=1800-∠1-∠BPF
∠A=1800-∠3-∠APE
∠BPF=∠APE
.
八字藏其中
∠1=∠2
.
.
即:∠FBE=∠ABD
等量加等量,其和相等
.
(ASA)
≌
.
D
B
2
A
E
F
P
1
3
识别模型,描出模型
A
C
D
E
B
∠CBA+ ∠DBA = ∠EBD+ ∠DBA=1200
∠CBA= ∠EBD= 60°
CB= AB
DB = EB
∠CBD= ∠ABE
4、如图,已知:点C、B、E在同一条直线上,ΔABC和ΔBDE是等边三角形。求证: ∠EAB= ∠DCB
∠EAB= ∠DCB
ΔCBD ≌ ΔABE
识别模型,描出模型
问题:再找一个600
八字出等角
A
C
D
E
B
G
H
变式1: 如图,已知△ABC和△DEB等边三角形 。
C,B,E在一条直线上。 求证: BG = BH。
识别全等,描出全等:
法1:ΔEBG ≌ ΔDBH(ASA)
法2:ΔBGA ≌ ΔBHC(ASA)
D
E
变式2:如图,△ABC和△CDE都是等边三角形,
A
B
C
识别模型,描出模型
5.如图,在 △ABC中,∠BAC=90°,AB=AC,∠ABC的平分线交AC于点D,过点C作BD的垂线交BD的延长线于点E,交BA的延长线于点F.求证:BD=2CE.
3个基本模型: (1) 8字型------∠ABD=∠ECD
(2) 二线合一-----等腰三角形------三线合一-----CF=2CE
(3)全等模型---------ΔABD ≌ ΔACF(ASA)---------BD=CF
任何几何难题的解决,最终必回到基本图形,基本规律,基本知识
识别模型,描出模型
6.将两个全等的直角三角形按如图所示叠放,AD与BC交于点E. 若AC=6,BC=10,求BE的长.
A
B
C
D
E
识别模型,描出模型:
全等模型:ΔABC≌ ΔBAD
∠1=∠2
1
2
BD=AC=6
AE=BE
AD=BC=10
AD-AE=BC-BE,即CE=ED= x
x
10-x
6
x
10-x
6
x2+62=(10-x)2
x=3.2
BE=10-3.2=6.8
等腰三角形模型
直角三角形模型
7.如图,D、E分别是等边三角形ABC的两边AB、AC上的点,且AD=CE,BE,DC相交于点P,求∠BPD的度数
从千差万别的汤中识别永恒不变的数学原理的药
全等藏其中
ΔACD≌ ΔCBE (SAS)
ΔBCD≌ ΔABE (SAS)
∠BPD=x+(60-x)=600
X
X
60-X
全等出等角、等边
描出基本图形,并写出相应的结论
8.如图,△ABC中,∠ABC,∠ACB的平分线相交于O,MN过点O且与BC平行,△ABC的周长为20,△AMN的周长为12,求BC的长
角平分线+平行=等腰三角形
BM=OM
CN=ON
C△AMN=AM+MN+AN=(AM+BM)+(CN+AN)=AB+BC=12
MN=OM+ON=BM+CN
BC=C△ABC - (AB+BC)=C△AMN - C△ABC=20-12=8
BC的长-----周长差
描出基本图形,并写出相应的结论
9.如图,在锐角三角形ABC中,AB=4,△ABC的面积为10,BD平分 ∠ABC,若M、N分别是BD、BC上的动点,求CM+MN的最小值
基本模型:将军饮马+斜大于直
┗
F
AB边上的高线CF就是CM+MN的最小值
N
'
CM+MN最小值=CF=10×2÷4=5
画出最小值
10.如图,E是等边三角形ABC中AC边上的点,∠1=∠2,BE=CD,则△ADE的形状是( )
A.一般等腰三角形 B.等边三角形
C.不等边三角形 D.不能确定形状
【解】 ∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°.
又∵∠1=∠2,BE=CD, ∴△ABE≌△ACD(SAS)..
∴AE=AD,∠CAD=∠BAE=60°.
∴△ADE是等边三角形.
B
关键点-------描出全等三角形
11. 如图,在△ABC中,AC=5,AB=7,AD平分∠BAC,DE⊥AC,DE=2,求△ABC的面积
角平分线模型-------图中有角平分线,可向两边作垂线
┗
F
DF=DE=2
S△ABC=S△ABD+S△ACD
=5+7=12
=
.
12.如图,CD是等腰三角形 △ABC底边上的中线,BE平分∠ABC,交CD于点E,AC=8,DE=2,求△ BCE的面积
┗
F
┗
基本模型:等腰三角形模型 + 角平分线模型
S△BCE=8×2÷2=8
BC=AC=8
EF=DE=2
图中有角平分线,可向两边作垂线
13.如图,△ABC 中,∠BAC=1300 ,AB ,AC 的垂直平分线分别交 BC于点E,F,与 AB ,AC 分别交于点D,G,求∠EAF 的度数
垂直平分线--------等腰三角形
∠B+∠C=1800-∠BAC
=1800-1300=500
AE=BE
AF=CF
∠B=∠EAB
∠C=∠FAG
∠EAB+∠FAG=∠B+∠C=500
∠EAF= ∠BAC - (∠EAB+∠FAG)
=1300-500=800
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
