浙教版九年级上册3.1 圆 课件(18张PPT)
文档属性
| 名称 | 浙教版九年级上册3.1 圆 课件(18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-25 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
3.1 圆(1)
以旧友
会新知
回首旧友
相关概念
定义:由不在同一条直线上的三条线段
首尾顺次相接所组成的图形叫做三角形.
△ABC
点
边
角
三角形的三要素
相关的线
角平分线
中线
高线
A
B
C
操作探索
画一个半径为2cm的圆.
任务1:学校举办秋季运动会,需要在平坦的操场上画一个半径为3m的圆,你有什么办法
新知探求
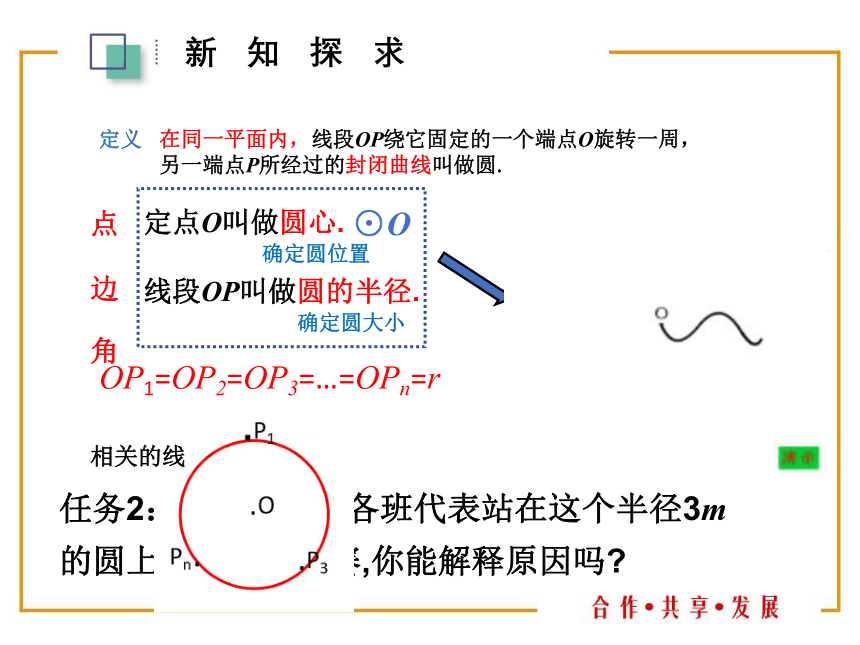
定义
线段OP绕它固定的一个端点O旋转一周,
另一端点P所经过的封闭曲线叫做圆.
在同一平面内,
点
边
角
定点O叫做圆心.
线段OP叫做圆的半径.
⊙O
确定圆位置
确定圆大小
任务2:运动会上,各班代表站在这个半径3m的圆上进行套圈比赛,你能解释原因吗
OP1=OP2=OP3=…=OPn=r
相关的线
新知探求
相
关
的
线
直线型
曲线型
弦:连结圆上任意
两点的线段叫做弦.
经过圆心的弦BD叫做直径.
圆弧
圆上任意两点间的部分叫做圆弧,简称弧.
半圆
劣弧
优弧
新知探求
A
B
C
D
E
F
A
B
C
能够重合的两个三角形叫做全等三角形.
O1
r
O2
r
能够重合的两个圆叫做全等圆.
问题1:为什么能重合?
问题2:大小相同意味着什么?
圆的大小相同
圆的半径相等
半径相等的两个圆叫做等圆.
新知探求
A
B
C
D
E
F
A
B
C
能够重合的两个三角形叫做全等三角形.
O1
r
O2
r
能够重合的两个圆叫做全等圆.
问题1:为什么能重合?
问题2:大小相同意味着什么?
圆的大小相同
圆的半径相等
半径相等的两个圆叫做等圆.
能够重合的圆弧称为相等的弧.
新知巩固
1、下列命题中,哪些是真命题?哪些是假命题?
(1)弦是直径;
(2)圆上的任意两点都能将圆分成一条劣弧和一条优弧;
(4)半径相等的圆一定能重合.
(3)圆中优弧所对的弦一定比劣弧所对的弦长;
假命题
假命题
假命题
真命题
它的逆命题呢?
特性运用
2.已知⊙O的面积为25π.
①若PO=5.5,则点P在圆_____________;
②若PO=4,则点P在圆_______________;
③若PO=_____________ ,则点P在圆上.
外
内
5
特性运用
例:如图,点A处有一空投,在A处正北方向60米的B处有一玩家,正西80米
的C处也有一玩家,在BC的中点D也有一玩家.假设他们移动速度相等,
请问谁先抢到空投?
特性拓展
变式1:如图,点A处是一房区,那附近有一敌方队伍,在房区A处正北方向
60米的B处有一己方队友,正西80米的C处也有一队友,在BC的中点D也有
一队友.现使用无人机对房区进行轰炸,以打击敌方队伍,请问怎么控制
爆炸范围才能不误伤队友?
特性生长
变式2:如图,点A处是一房区,那附近有一敌方队伍,在房区A处正北方向
60米的B处有一己方队友,正西80米的C处也有一队友,队友D
在BC线段上进行往返奔跑勘察,现使用无人机对房区进行轰炸,
以打击敌方队伍,请问怎么控制爆炸范围才能不误伤队友?
特性生长
变式2:如图,点A处是一房区,那附近有一敌方队伍,在房区A处正北方向
60米的B处有一己方队友,正西80米的C处也有一队友,队友D
在BC线段上进行往返奔跑勘察,现使用无人机对房区进行轰炸,
以打击敌方队伍,请问怎么控制爆炸范围才能不误伤队友?
生
长
数
学
学
生
命
成
长
3.1 圆(1)
以旧友
会新知
回首旧友
相关概念
定义:由不在同一条直线上的三条线段
首尾顺次相接所组成的图形叫做三角形.
△ABC
点
边
角
三角形的三要素
相关的线
角平分线
中线
高线
A
B
C
操作探索
画一个半径为2cm的圆.
任务1:学校举办秋季运动会,需要在平坦的操场上画一个半径为3m的圆,你有什么办法
新知探求
定义
线段OP绕它固定的一个端点O旋转一周,
另一端点P所经过的封闭曲线叫做圆.
在同一平面内,
点
边
角
定点O叫做圆心.
线段OP叫做圆的半径.
⊙O
确定圆位置
确定圆大小
任务2:运动会上,各班代表站在这个半径3m的圆上进行套圈比赛,你能解释原因吗
OP1=OP2=OP3=…=OPn=r
相关的线
新知探求
相
关
的
线
直线型
曲线型
弦:连结圆上任意
两点的线段叫做弦.
经过圆心的弦BD叫做直径.
圆弧
圆上任意两点间的部分叫做圆弧,简称弧.
半圆
劣弧
优弧
新知探求
A
B
C
D
E
F
A
B
C
能够重合的两个三角形叫做全等三角形.
O1
r
O2
r
能够重合的两个圆叫做全等圆.
问题1:为什么能重合?
问题2:大小相同意味着什么?
圆的大小相同
圆的半径相等
半径相等的两个圆叫做等圆.
新知探求
A
B
C
D
E
F
A
B
C
能够重合的两个三角形叫做全等三角形.
O1
r
O2
r
能够重合的两个圆叫做全等圆.
问题1:为什么能重合?
问题2:大小相同意味着什么?
圆的大小相同
圆的半径相等
半径相等的两个圆叫做等圆.
能够重合的圆弧称为相等的弧.
新知巩固
1、下列命题中,哪些是真命题?哪些是假命题?
(1)弦是直径;
(2)圆上的任意两点都能将圆分成一条劣弧和一条优弧;
(4)半径相等的圆一定能重合.
(3)圆中优弧所对的弦一定比劣弧所对的弦长;
假命题
假命题
假命题
真命题
它的逆命题呢?
特性运用
2.已知⊙O的面积为25π.
①若PO=5.5,则点P在圆_____________;
②若PO=4,则点P在圆_______________;
③若PO=_____________ ,则点P在圆上.
外
内
5
特性运用
例:如图,点A处有一空投,在A处正北方向60米的B处有一玩家,正西80米
的C处也有一玩家,在BC的中点D也有一玩家.假设他们移动速度相等,
请问谁先抢到空投?
特性拓展
变式1:如图,点A处是一房区,那附近有一敌方队伍,在房区A处正北方向
60米的B处有一己方队友,正西80米的C处也有一队友,在BC的中点D也有
一队友.现使用无人机对房区进行轰炸,以打击敌方队伍,请问怎么控制
爆炸范围才能不误伤队友?
特性生长
变式2:如图,点A处是一房区,那附近有一敌方队伍,在房区A处正北方向
60米的B处有一己方队友,正西80米的C处也有一队友,队友D
在BC线段上进行往返奔跑勘察,现使用无人机对房区进行轰炸,
以打击敌方队伍,请问怎么控制爆炸范围才能不误伤队友?
特性生长
变式2:如图,点A处是一房区,那附近有一敌方队伍,在房区A处正北方向
60米的B处有一己方队友,正西80米的C处也有一队友,队友D
在BC线段上进行往返奔跑勘察,现使用无人机对房区进行轰炸,
以打击敌方队伍,请问怎么控制爆炸范围才能不误伤队友?
生
长
数
学
学
生
命
成
长
同课章节目录
