含字母系数一元一次不等式的复习

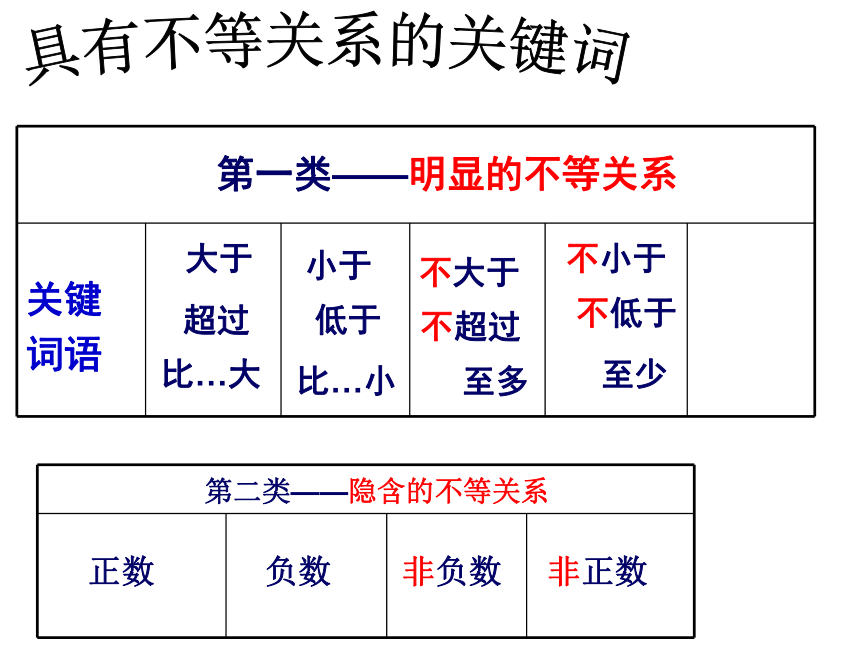
课件11张PPT。第三章：一元一次不等式第一类——明显的不等关系比…大大于小于 至多不大于不超过不小于不低于 至少超过低于比…小具有不等关系的关键词基础巩固画数轴的方法：1、大于向右，小于向左2、有等号取实心，无等号取空心找数轴上公共部分的口诀：大大取大，小小取小，大小小大取中间，大大小小则无解引入字母系数一、解集对照法例1. 关于x的不等式组的解集是，则=______________ -3m-2例2.如果不等式组的取值范围是（ ）
C变式练习 B例3.若不等式组1方法总结：
解集对照法中，最关键的在于“对”，即在含字母系数的代数式与给出的解集之间建立对应关系，从而确定字母系数的值或取值范围.二、借助数轴法例4.已知不等式组 ⑴要使不等式组有解，k的取值范围是____________
⑵要使不等式组无解，k的取值范围是____________变式练习例5. 如图是表示某个不等式组的解集,
则该不等式组的整数解的个数是（ ）
A. 4 B. 5
C. 6 D. 7C变式练习方法总结:
把已知或能算出的解表示在数轴上, 让带字母系数的解在数轴上移动,观察何时满足题目要求,尤其注意界点能否取到.某电影院，为了吸引学生观众，增加票房收入，决定在六月份向中，小学生预售七，八两个月的“学生电影（优惠）兑换券”，每张优惠券定价为1元，可随时兑换当日某一电影票一张。 如果七，八月期间，每天放映5场次，电影票每张3元，平均每场次能卖出25张，为了保证每场次的票房收入平均不低于1000元，至少应预售这两个月的“优惠券”多少张？应用范例不等关系是什么？本节课你有什么收获？