抛物线的图形变换

课件14张PPT。二次函数复习——让我们学会
以“不变”
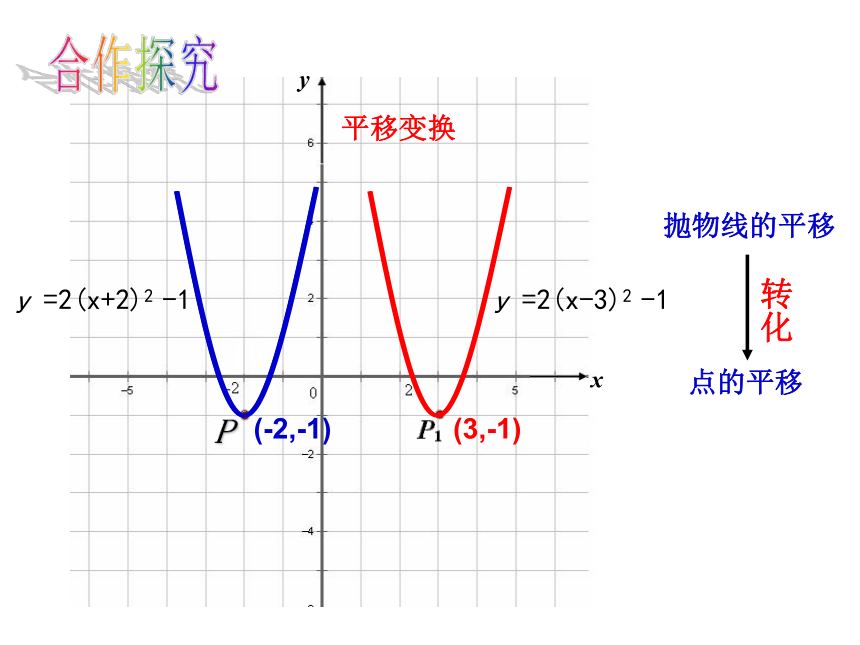
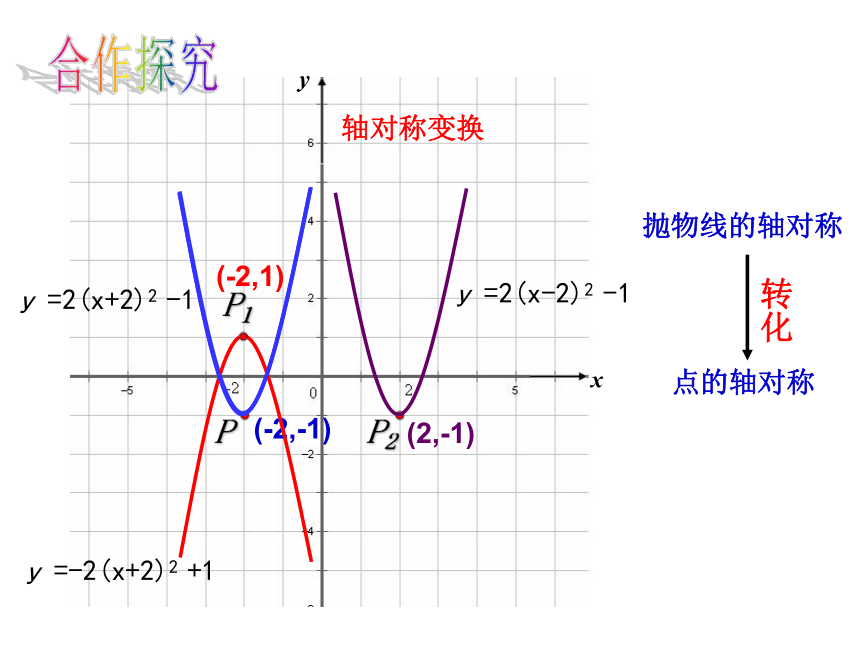
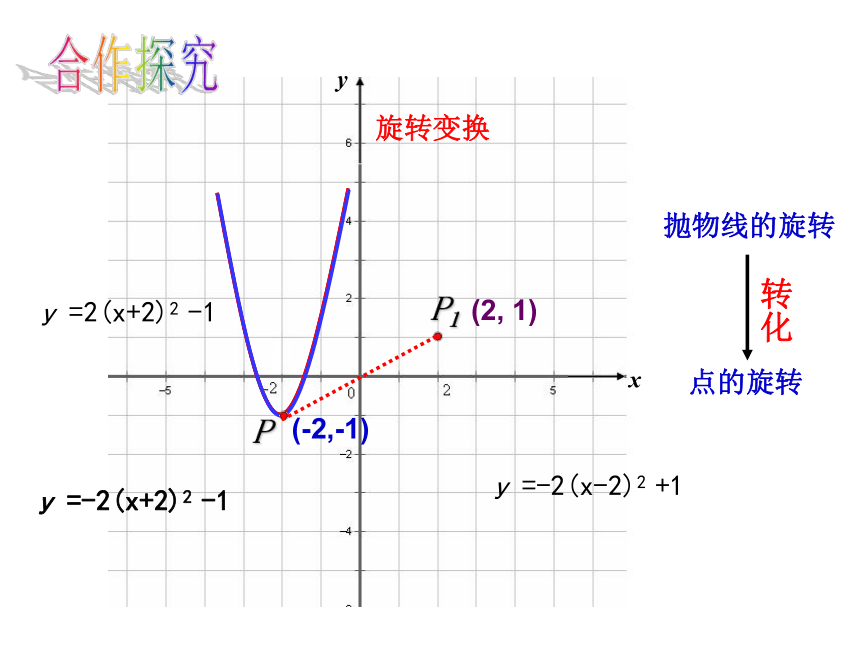
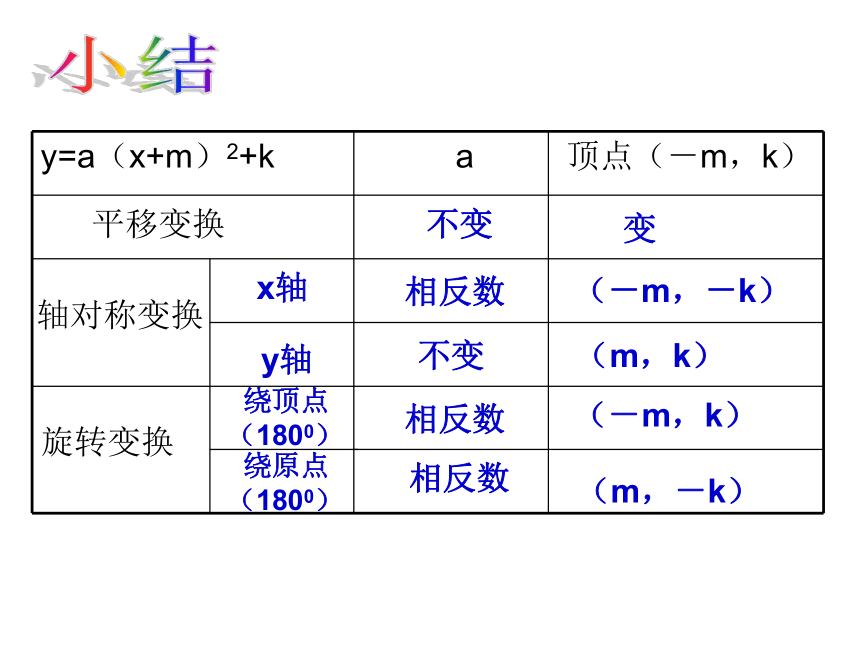
应“万变”变换中的抛物线平移变换点的平移xy抛物线的平移(-2,-1)(3,-1)合作探究P y =2(x+2)2 -1 y =2(x-3)2 -1转化轴对称变换xy(-2,-1)P y =2(x+2)2 -1P2(2,-1)点的轴对称抛物线的轴对称转化P1(-2,1) y =-2(x+2)2 +1 y =2(x-2)2 -1合作探究旋转变换xy(-2,-1)P y =2(x+2)2 -1点的旋转抛物线的旋转转化P1(2, 1) y =-2(x+2)2 -1 y =-2(x-2)2 +1合作探究平移变换不变变轴对称变换旋转变换（－m，k）（－m，－k）（m，k）（m，－k）x轴y轴相反数不变 绕顶点（1800）相反数相反数 绕原点（1800）小结1.抛物线 可由抛物线 向 平移 个单位得到 左3向左平移2个单位再向上平移1个单位2.将抛物线y=x2-4x+3
则平移后的抛物线
顶点为原点
练习体验__________________________________________________________变式:顶点为原点改为经过原点3.已知二次函数 .
D练习体验(0,3)(0,-3) 4.已知二次函数 .练习体验将图象绕原点旋转180°后得到的函数图象的解析式为______________.
y=2（x+3）2－1变式：将图象绕点（0,1）旋转180°后得到的函数图象的解析式为______________.
y=－2（x-3）2+1xyPAy=2（x+3）2－1y=-2（x-3）2+3(-3,-1)(3,3)HH 将抛物线y=x2向下平移若干个单位，平移后交x轴于A、B两点，交y轴于点C,若△ABC是等边三角形.
（1）求出平移后的抛物线的解析式.ABCxyy=x2o应用拓展·（2）点Q是x轴正半轴上一点,将抛物线绕Q旋转180°后得到新抛物线，顶点为N，与x轴相交于E、F两点（点E在点F的左边），当以点C、N、F为顶点的三角形是直角三角形时，求点Q的坐标．OxyC应用拓展AB在研究过程中有何体会?学习梳理今天我们收获是什么?“做一题，知一类，会一片”xyo（3）将平移后抛物线的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当直线y=x+b与此图象有两个公共点时，求b的取值范围.
CAB课外拓展y=x+b