与圆及圆锥有关的计算
图片预览



文档简介
与圆的弧长及圆锥有关的计算
【知识要点】
1. 圆的周长为 ,1°的圆心角所对的弧长为 ,n°的圆心角所对的弧长为 ,弧长公式为 .
2. 圆的面积为 ,1°的圆心角所在的扇形面积为 ,n°的圆心角所在的扇形面积为S= = = .
3. 圆柱的侧面积公式:S=.(其中为 的半径,为 的高)
4. 圆锥的侧面积公式:S=.(其中为 的半径,为 的长)
圆锥的全面积公式为: .
圆锥的侧面展开图是 ,这个扇形的半径等于 弧长等于圆锥的
例1:写出扇形弧长公式和面积公式,并证明。
即时训练:(2013兰州)圆锥底面圆的半径为3m,其侧面展开图是半圆,则圆锥母线长为( )
A.3cm B.6cm C.9cm D.12cm
即时训练:(2013湖州)在学校组织的实践活动中,小新同学用纸板制作了一个圆锥模型,它的底面半径为1,高为,则这个圆锥的侧面积为( )
A.4π B.3π C.π D.2π
即时训练:(2013杭州)四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=2,AB=3,把梯形ABCD分别绕直线AB,CD旋转一周,所得几何体的表面积分别为S1,S2,则|S1﹣S2|= (平方单位)
例2:扇形的圆心角为,半径为,,是的三等分点,则图中阴影部分的面积和是。
即时训练:(2013山西)如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )
- B.- C.π- D.π-
即时训练:(2013广东省)如图,三个小正方形的边长都为1,则图中阴影部分面积的和是 .(结果保留)
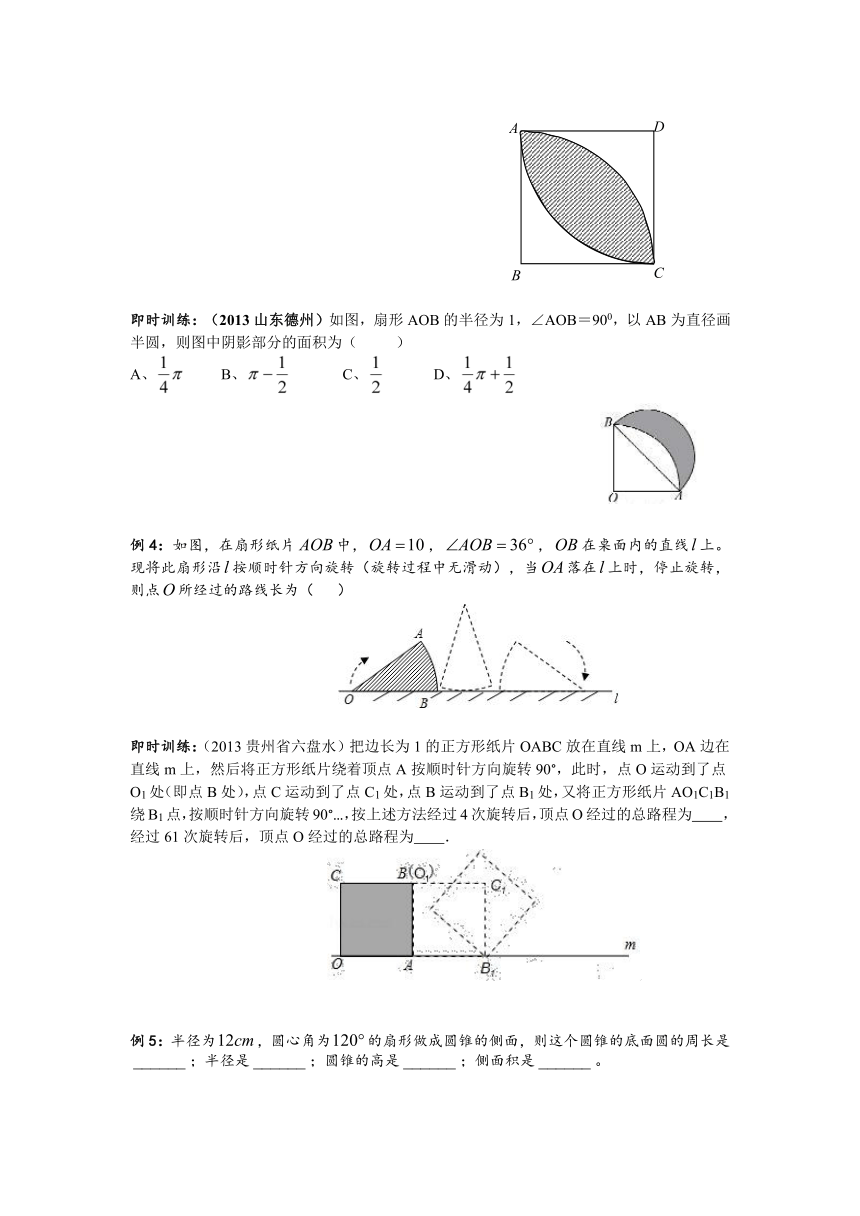
例3:已知的边长为,以各边为直径在正方形内画圆周,则所围成的阴影部分的面积是多少?
即时训练:(2013 东营)如图,正方形ABCD中,分别以B、D为圆心,以正方形
的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )
B. C. D.
即时训练:(2013山东德州)如图,扇形AOB的半径为1,∠AOB=900,以AB为直径画半圆,则图中阴影部分的面积为( )
B、 C、 D、
例4:如图,在扇形纸片中,,,在桌面内的直线上。现将此扇形沿按顺时针方向旋转(旋转过程中无滑动),当落在上时,停止旋转,则点所经过的路线长为( )
即时训练:(2013贵州省六盘水)把边长为1的正方形纸片OABC放在直线m上,OA边在直线m上,然后将正方形纸片绕着顶点A按顺时针方向旋转90°,此时,点O运动到了点O1处(即点B处),点C运动到了点C1处,点B运动到了点B1处,又将正方形纸片AO1C1B1绕B1点,按顺时针方向旋转90°…,按上述方法经过4次旋转后,顶点O经过的总路程为 ,经过61次旋转后,顶点O经过的总路程为 .
例5:半径为,圆心角为的扇形做成圆锥的侧面,则这个圆锥的底面圆的周长是;半径是;圆锥的高是;侧面积是。
即时训练:(2013湖北孝感)用半径为10cm,圆心角为216°的扇形做成一个圆锥的侧面,则这个圆锥的高为 cm.
即时训练:(2013湖南郴州)圆锥的侧面积为6πcm2,底面圆的半径为2cm,则这个圆锥的母线长为 cm.
即时训练:(2013·聊城)已知一个扇形的半径为60cm,圆心角为150°,用它围成一个圆锥的侧面,那么圆锥的底面半径为 cm.
例6:在中,,,,将三角形以为轴旋转一周,求所得的圆锥的表面积和体积。
即时训练:如图,若圆的直径与弦的夹角为,切线与的延长线交于点,且圆的半径为,将三角形以为轴旋转一周,求所得的圆锥的表面积和体积。
例7:如图,圆锥的轴截面是边长为的正三角形,是母线的中点,
求:(1)在圆锥的侧面上从点到点的最短路线的长;(2)在圆锥的侧面上从点回到点的最短路线的长;(3)在圆锥的侧面上从点爬到母线中点的最段路线的长。
即时训练:交圆于点、,交圆于点、,如弧,弧,则的度数为。
思考:如图中,弦与直径的夹角为,交点为点。若,则圆的半径为。
练习
1、如图,、是上的两个点,是直径,若,则的度数是( )
2、如图,、、、四点在上,四边形的一个外角,则等于( )
A、35° B、70° C、110° D、140°
3、已知如图、是的两条直径,弦//,求证:。
4、已知:如图所示,点是外的一点,与相交于点、,与 相交于、,。
求证:(1)平分;
(2);
(3)。
5、已知、为圆的两直径,弦平行,弧的度数为,求的度数。
6、如图,,,的大小关系。
7、如图,正方形内接于,为的中点,直线交于点,如果 的半径为,则点到的距离( )
A、 B、 C、 D、
8、内接于圆,,弦//,
求证:①平分;
②。
9、如图,已知、两点的坐标分别为、,是外接圆上的一点,且,则点的坐标为。
10、用三种方法证明:如图,已知在中,半径,是延长线上一点, 交于,求证:弧的度数是的倍。
11、如图,已知的两条半径与互相垂直,为上的一点,且,求的度数。
12、如图,为半圆的直径,,,…,是半圆上的个点,满足
,对于线段,,…,,,,…,,当时,有对互相平行的线段;当取任意大于的整数时,试探索这条线段中有多少对互相平行的线段,写出你的结论。
13、如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,点P是直径MN上一个动点,则PA+PB的最小值为( )
A、2 B、 C、1 D、2
14、如图,为半圆的直径,半径, 为的中点,过点作//,
求证:(1)四边形为菱形;(2)。
15、已知的半径,扇形的面积等于,则弧所对的圆周角的度数是( )
A、120° B、90° C、60° D、30°
16、如图,把直角三角形的斜边放在定直线上,按顺时针方向在上转动两次,使它转到的位置。若,,则顶点运动到点的位置时,点两次运动所经过的路程是______。(计算结果不取近似值)
17、在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若扇形的半径为,圆心角为,则圆的半径为________。
18、圆锥的轴截面是一个等边三角形,则这个圆锥的底面积、侧面积、表面积的比是______。
19、如图,有一直径为的圆形铁皮,要从中剪出一个最大的圆心角是的扇形。
(1)求剪掉部分即阴影部分的面积(结果保留π);
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面半径是多少?
20、如图,在正方形铁皮上剪下圆形和扇形,使之恰好围成如图所示的圆锥模型,设圆的半径为,扇形的半径为,则圆半径与扇形半径之间的关系是( )
A、 B、 C、 D、
21、如图,扇形OAB的圆心角为90°,分别以OA,OB为直径在扇形内作半圆,P和Q分别表示两个阴影部分的面积。
(1)P和Q的面积之和;
(2)猜想P和Q的面积大小关系?并说明理由。
6、经过一个带盖的圆锥形容器的轴的剖面是一个等腰三角形(如图a),它的腰长等于圆锥的
母线长,底边长等于圆锥底面的直径,其尺寸如图a所示(单位:)。
(1)求圆锥形容器的侧面积和它的侧面展开图的圆心角α;
(2)图b是一个直径等于的半圆形铁皮,如何把它裁剪,可以做成这个带盖的圆锥形容器(不考虑缝接处的用料,在图b中用虚线画出裁剪线,注明必要的角度、线段长;画图工具不限,不要求写画法)。
A
B
C
D
【知识要点】
1. 圆的周长为 ,1°的圆心角所对的弧长为 ,n°的圆心角所对的弧长为 ,弧长公式为 .
2. 圆的面积为 ,1°的圆心角所在的扇形面积为 ,n°的圆心角所在的扇形面积为S= = = .
3. 圆柱的侧面积公式:S=.(其中为 的半径,为 的高)
4. 圆锥的侧面积公式:S=.(其中为 的半径,为 的长)
圆锥的全面积公式为: .
圆锥的侧面展开图是 ,这个扇形的半径等于 弧长等于圆锥的
例1:写出扇形弧长公式和面积公式,并证明。
即时训练:(2013兰州)圆锥底面圆的半径为3m,其侧面展开图是半圆,则圆锥母线长为( )
A.3cm B.6cm C.9cm D.12cm
即时训练:(2013湖州)在学校组织的实践活动中,小新同学用纸板制作了一个圆锥模型,它的底面半径为1,高为,则这个圆锥的侧面积为( )
A.4π B.3π C.π D.2π
即时训练:(2013杭州)四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=2,AB=3,把梯形ABCD分别绕直线AB,CD旋转一周,所得几何体的表面积分别为S1,S2,则|S1﹣S2|= (平方单位)
例2:扇形的圆心角为,半径为,,是的三等分点,则图中阴影部分的面积和是。
即时训练:(2013山西)如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )
- B.- C.π- D.π-
即时训练:(2013广东省)如图,三个小正方形的边长都为1,则图中阴影部分面积的和是 .(结果保留)
例3:已知的边长为,以各边为直径在正方形内画圆周,则所围成的阴影部分的面积是多少?
即时训练:(2013 东营)如图,正方形ABCD中,分别以B、D为圆心,以正方形
的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )
B. C. D.
即时训练:(2013山东德州)如图,扇形AOB的半径为1,∠AOB=900,以AB为直径画半圆,则图中阴影部分的面积为( )
B、 C、 D、
例4:如图,在扇形纸片中,,,在桌面内的直线上。现将此扇形沿按顺时针方向旋转(旋转过程中无滑动),当落在上时,停止旋转,则点所经过的路线长为( )
即时训练:(2013贵州省六盘水)把边长为1的正方形纸片OABC放在直线m上,OA边在直线m上,然后将正方形纸片绕着顶点A按顺时针方向旋转90°,此时,点O运动到了点O1处(即点B处),点C运动到了点C1处,点B运动到了点B1处,又将正方形纸片AO1C1B1绕B1点,按顺时针方向旋转90°…,按上述方法经过4次旋转后,顶点O经过的总路程为 ,经过61次旋转后,顶点O经过的总路程为 .
例5:半径为,圆心角为的扇形做成圆锥的侧面,则这个圆锥的底面圆的周长是;半径是;圆锥的高是;侧面积是。
即时训练:(2013湖北孝感)用半径为10cm,圆心角为216°的扇形做成一个圆锥的侧面,则这个圆锥的高为 cm.
即时训练:(2013湖南郴州)圆锥的侧面积为6πcm2,底面圆的半径为2cm,则这个圆锥的母线长为 cm.
即时训练:(2013·聊城)已知一个扇形的半径为60cm,圆心角为150°,用它围成一个圆锥的侧面,那么圆锥的底面半径为 cm.
例6:在中,,,,将三角形以为轴旋转一周,求所得的圆锥的表面积和体积。
即时训练:如图,若圆的直径与弦的夹角为,切线与的延长线交于点,且圆的半径为,将三角形以为轴旋转一周,求所得的圆锥的表面积和体积。
例7:如图,圆锥的轴截面是边长为的正三角形,是母线的中点,
求:(1)在圆锥的侧面上从点到点的最短路线的长;(2)在圆锥的侧面上从点回到点的最短路线的长;(3)在圆锥的侧面上从点爬到母线中点的最段路线的长。
即时训练:交圆于点、,交圆于点、,如弧,弧,则的度数为。
思考:如图中,弦与直径的夹角为,交点为点。若,则圆的半径为。
练习
1、如图,、是上的两个点,是直径,若,则的度数是( )
2、如图,、、、四点在上,四边形的一个外角,则等于( )
A、35° B、70° C、110° D、140°
3、已知如图、是的两条直径,弦//,求证:。
4、已知:如图所示,点是外的一点,与相交于点、,与 相交于、,。
求证:(1)平分;
(2);
(3)。
5、已知、为圆的两直径,弦平行,弧的度数为,求的度数。
6、如图,,,的大小关系。
7、如图,正方形内接于,为的中点,直线交于点,如果 的半径为,则点到的距离( )
A、 B、 C、 D、
8、内接于圆,,弦//,
求证:①平分;
②。
9、如图,已知、两点的坐标分别为、,是外接圆上的一点,且,则点的坐标为。
10、用三种方法证明:如图,已知在中,半径,是延长线上一点, 交于,求证:弧的度数是的倍。
11、如图,已知的两条半径与互相垂直,为上的一点,且,求的度数。
12、如图,为半圆的直径,,,…,是半圆上的个点,满足
,对于线段,,…,,,,…,,当时,有对互相平行的线段;当取任意大于的整数时,试探索这条线段中有多少对互相平行的线段,写出你的结论。
13、如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,点P是直径MN上一个动点,则PA+PB的最小值为( )
A、2 B、 C、1 D、2
14、如图,为半圆的直径,半径, 为的中点,过点作//,
求证:(1)四边形为菱形;(2)。
15、已知的半径,扇形的面积等于,则弧所对的圆周角的度数是( )
A、120° B、90° C、60° D、30°
16、如图,把直角三角形的斜边放在定直线上,按顺时针方向在上转动两次,使它转到的位置。若,,则顶点运动到点的位置时,点两次运动所经过的路程是______。(计算结果不取近似值)
17、在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若扇形的半径为,圆心角为,则圆的半径为________。
18、圆锥的轴截面是一个等边三角形,则这个圆锥的底面积、侧面积、表面积的比是______。
19、如图,有一直径为的圆形铁皮,要从中剪出一个最大的圆心角是的扇形。
(1)求剪掉部分即阴影部分的面积(结果保留π);
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面半径是多少?
20、如图,在正方形铁皮上剪下圆形和扇形,使之恰好围成如图所示的圆锥模型,设圆的半径为,扇形的半径为,则圆半径与扇形半径之间的关系是( )
A、 B、 C、 D、
21、如图,扇形OAB的圆心角为90°,分别以OA,OB为直径在扇形内作半圆,P和Q分别表示两个阴影部分的面积。
(1)P和Q的面积之和;
(2)猜想P和Q的面积大小关系?并说明理由。
6、经过一个带盖的圆锥形容器的轴的剖面是一个等腰三角形(如图a),它的腰长等于圆锥的
母线长,底边长等于圆锥底面的直径,其尺寸如图a所示(单位:)。
(1)求圆锥形容器的侧面积和它的侧面展开图的圆心角α;
(2)图b是一个直径等于的半圆形铁皮,如何把它裁剪,可以做成这个带盖的圆锥形容器(不考虑缝接处的用料,在图b中用虚线画出裁剪线,注明必要的角度、线段长;画图工具不限,不要求写画法)。
A
B
C
D
同课章节目录
