圆的基本性质(一)——垂径定理、弦、圆心角和圆周角
文档属性
| 名称 | 圆的基本性质(一)——垂径定理、弦、圆心角和圆周角 |  | |
| 格式 | zip | ||
| 文件大小 | 70.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-23 09:28:49 | ||
图片预览


文档简介
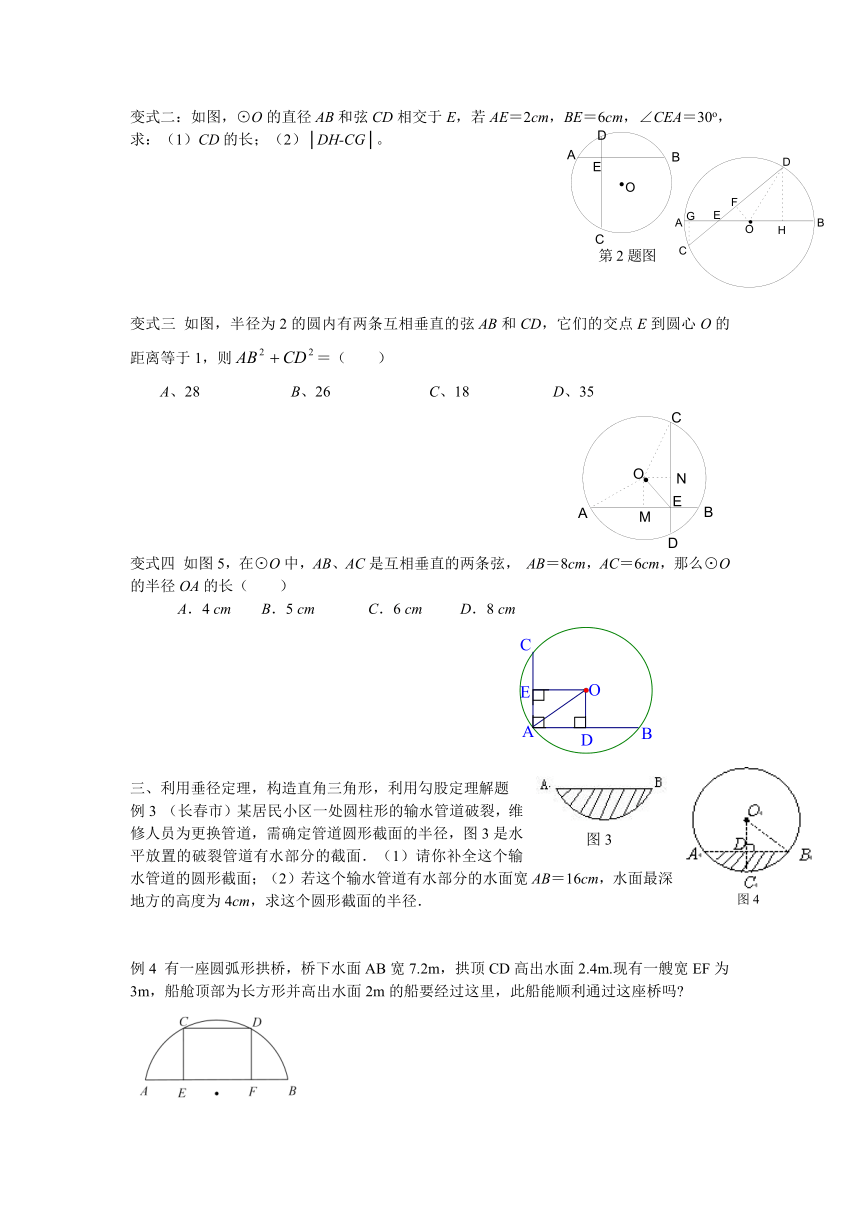
圆的基本性质(一)——垂径定理、弦、圆心角和圆周角
垂径定理及推论:对于一个圆和一条直线来说,如果具备下列四个条件中的任何两个,那么也具有其它三个:①垂直于弦,②过圆心,③平分弦,④平分弦所对的弧(当以①、③为题设时,“弦”不能是直径)。
典型例题
一、利用垂径平分弦所对的弧,来处理角的关系
例1 如图1,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于( )
A.80° B. 50° C. 40° D. 20°
二、利用垂径垂直平分弦,证相有关线段相等
例2如图,AB为⊙O的直径,CD为弦,过C、D分别作CN⊥CD、DM⊥CD,分别交AB于N、M,请问图中的AN与BM是否相等,说明理由.
变式一:变式二:
例3 如图2,矩形ABCD与圆心在AB上的⊙O交于点G、B、F、E, GB=8cm,AG=1cm,DE=2cm,则EF= cm .
变式一:圆内两条互相平行的弦AB、CD,其中AB=16cm,CD=12cm,圆的半径为10,求AB、CD间的距离。
变式二:如图,⊙O的直径AB和弦CD相交于E,若AE=2cm,BE=6cm,∠CEA=30o,求:(1)CD的长;(2)│DH-CG│。
变式三 如图,半径为2的圆内有两条互相垂直的弦AB和CD,它们的交点E到圆心O的距离等于1,则=( )
A、28 B、26 C、18 D、35
变式四 如图5,在⊙O中,AB、AC是互相垂直的两条弦, AB=8cm,AC=6cm,那么⊙O的半径OA的长( )
A.4 cm B.5 cm C.6 cm D.8 cm
三、利用垂径定理,构造直角三角形,利用勾股定理解题
例3 (长春市)某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,图3是水平放置的破裂管道有水部分的截面.(1)请你补全这个输水管道的圆形截面;(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.
例4 有一座圆弧形拱桥,桥下水面AB宽7.2m,拱顶CD高出水面2.4m.现有一艘宽EF为3m,船舱顶部为长方形并高出水面2m的船要经过这里,此船能顺利通过这座桥吗
同步练习
1、在半径为5cm的⊙O中,有一点P满足OP=3 cm,则过P的整数弦有 条。
2、如图,⊙O中弦AB⊥CD于E,AE=2,EB=6,ED=3,则⊙O的半径为 。
3、等腰△ABC中,AB=AC,∠A=120o,BC=10 cm,则△ABC的外接圆半径为 。
4、圆内一弦与直径相交成30o的角,且分直径为1 cm和5 cm两段,则此弦长为 。
二、解答题:
1、如图,Rt△ABC中,∠C=90o,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB、BC分别交于点D、E,求AB、AD的长。
2、如图,⊙O的半径为10cm,G是直径AB上一点,弦CD经过点G,CD=16cm,AE⊥CD于E,BF⊥CD于F,求AE-BF的值。
3、如图,AB、AC为⊙O的两条弦,D、E分别为、中点,求证:AM=AN.
本资料由《七彩教育网》www. 提供!
课下练习
1. 已知:AB交圆O于C、D,且AC=BD.你认为OA=OB吗?为什么?
2. 如图所示,是一个直径为650mm的圆柱形输油管的横截面,若油面宽AB=600mm,求油面的最大深度。
3. 如图所示,AB是圆O的直径,以OA为直径的圆C与圆O的弦AD相交于点E。你认为图中有哪些相等的线段?为什么?
4. 如图所示,OA是圆O的半径,弦CD⊥OA于点P,已知OC=5,OP=3,则弦CD=________________。
5. 如图所示,在圆O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为D、E,若AC=2cm,则圆O的半径为____________cm。
6. 如图所示,AB是圆O的直径,弦CD⊥AB,E为垂足,若AB=9,BE=1,则CD=______________。
7. 如图所示,在△ABC中,∠C=90°,AB=10,AC=8,以AC为直径作圆与斜边交于点P,则BP的长为____________。
8. 如图所示,四边形ABCD内接于圆O,∠BCD=120°,则∠BOD=____________度。
9. 如图所示,圆O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是( ) A. 3≤OM≤5 B. 4≤OM≤5 C. 3<OM<5 D. 4<OM<5
10. 下列说法中,正确的是( )
A. 到圆心的距离大于半径的点在圆内 B. 圆的半径垂直于圆的切线
C. 圆周角等于圆心角的一半 D. 等弧所对的圆心角相等
11. 若圆的一条弦把圆分成度数的比为1:3的两条弧,则劣弧所对的圆周角等于( )
A. 45° B. 90° C. 135° D. 270°
12. 如图所示,A、B、C三点在圆O上,∠AOC=100°,则∠ABC等于( )
A. 140° B. 110° C. 120° D. 130°
13. △ABC中,∠C=90°,AB=,BC=,以点A为圆心,以长为半径画圆,则点C在圆A___________,点B在圆A_________;
14. 圆的半径等于,圆内一条弦长2,则弦的中点与弦所对弧的中点的距离等于_____________;
15. 如图所示,已知AB为圆O的直径,AC为弦,OD∥BC交AC于D,OD=,求BC的长;
16. 如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D。已知:AB,CD。(1)求作此残片所在的圆(不写作法,保留作图痕迹);(2)求(1)中所作圆的半径。
在△ABC中,∠C=90°,AC=BC=4cm,D是AB边的中点,以点C为圆心,4cm为半径作圆。则A、B、C、D四点在圆内有_____________。
如图所示,圆O的直径AB和弦CD交于E,已知AE=6cm,EB=2cm,∠CEA=30°,求CD。
第18题 第19题
19. 如图所示,已知O是∠EPF的平分线上的一点,以O为圆心的圆心角的两边分别交于点A、B、C、D求证:PB=PD,若角的顶点P在圆上或圆内,上述还成立吗?请说明。
参考答案1. 过点O作于E
2. 175mm 3. 略 4. 8 5. 6. 7. 3.6 8. 120 9. B
10. D 11. A 12. D13. 内部、外部 14. 15. BC=4cm 16. (2)
17. C、D 18. 19. (1)证明:过O作
(2)上述结论仍成立:
如图所示
图4
图3
垂径定理及推论:对于一个圆和一条直线来说,如果具备下列四个条件中的任何两个,那么也具有其它三个:①垂直于弦,②过圆心,③平分弦,④平分弦所对的弧(当以①、③为题设时,“弦”不能是直径)。
典型例题
一、利用垂径平分弦所对的弧,来处理角的关系
例1 如图1,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于( )
A.80° B. 50° C. 40° D. 20°
二、利用垂径垂直平分弦,证相有关线段相等
例2如图,AB为⊙O的直径,CD为弦,过C、D分别作CN⊥CD、DM⊥CD,分别交AB于N、M,请问图中的AN与BM是否相等,说明理由.
变式一:变式二:
例3 如图2,矩形ABCD与圆心在AB上的⊙O交于点G、B、F、E, GB=8cm,AG=1cm,DE=2cm,则EF= cm .
变式一:圆内两条互相平行的弦AB、CD,其中AB=16cm,CD=12cm,圆的半径为10,求AB、CD间的距离。
变式二:如图,⊙O的直径AB和弦CD相交于E,若AE=2cm,BE=6cm,∠CEA=30o,求:(1)CD的长;(2)│DH-CG│。
变式三 如图,半径为2的圆内有两条互相垂直的弦AB和CD,它们的交点E到圆心O的距离等于1,则=( )
A、28 B、26 C、18 D、35
变式四 如图5,在⊙O中,AB、AC是互相垂直的两条弦, AB=8cm,AC=6cm,那么⊙O的半径OA的长( )
A.4 cm B.5 cm C.6 cm D.8 cm
三、利用垂径定理,构造直角三角形,利用勾股定理解题
例3 (长春市)某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,图3是水平放置的破裂管道有水部分的截面.(1)请你补全这个输水管道的圆形截面;(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.
例4 有一座圆弧形拱桥,桥下水面AB宽7.2m,拱顶CD高出水面2.4m.现有一艘宽EF为3m,船舱顶部为长方形并高出水面2m的船要经过这里,此船能顺利通过这座桥吗
同步练习
1、在半径为5cm的⊙O中,有一点P满足OP=3 cm,则过P的整数弦有 条。
2、如图,⊙O中弦AB⊥CD于E,AE=2,EB=6,ED=3,则⊙O的半径为 。
3、等腰△ABC中,AB=AC,∠A=120o,BC=10 cm,则△ABC的外接圆半径为 。
4、圆内一弦与直径相交成30o的角,且分直径为1 cm和5 cm两段,则此弦长为 。
二、解答题:
1、如图,Rt△ABC中,∠C=90o,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB、BC分别交于点D、E,求AB、AD的长。
2、如图,⊙O的半径为10cm,G是直径AB上一点,弦CD经过点G,CD=16cm,AE⊥CD于E,BF⊥CD于F,求AE-BF的值。
3、如图,AB、AC为⊙O的两条弦,D、E分别为、中点,求证:AM=AN.
本资料由《七彩教育网》www. 提供!
课下练习
1. 已知:AB交圆O于C、D,且AC=BD.你认为OA=OB吗?为什么?
2. 如图所示,是一个直径为650mm的圆柱形输油管的横截面,若油面宽AB=600mm,求油面的最大深度。
3. 如图所示,AB是圆O的直径,以OA为直径的圆C与圆O的弦AD相交于点E。你认为图中有哪些相等的线段?为什么?
4. 如图所示,OA是圆O的半径,弦CD⊥OA于点P,已知OC=5,OP=3,则弦CD=________________。
5. 如图所示,在圆O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为D、E,若AC=2cm,则圆O的半径为____________cm。
6. 如图所示,AB是圆O的直径,弦CD⊥AB,E为垂足,若AB=9,BE=1,则CD=______________。
7. 如图所示,在△ABC中,∠C=90°,AB=10,AC=8,以AC为直径作圆与斜边交于点P,则BP的长为____________。
8. 如图所示,四边形ABCD内接于圆O,∠BCD=120°,则∠BOD=____________度。
9. 如图所示,圆O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是( ) A. 3≤OM≤5 B. 4≤OM≤5 C. 3<OM<5 D. 4<OM<5
10. 下列说法中,正确的是( )
A. 到圆心的距离大于半径的点在圆内 B. 圆的半径垂直于圆的切线
C. 圆周角等于圆心角的一半 D. 等弧所对的圆心角相等
11. 若圆的一条弦把圆分成度数的比为1:3的两条弧,则劣弧所对的圆周角等于( )
A. 45° B. 90° C. 135° D. 270°
12. 如图所示,A、B、C三点在圆O上,∠AOC=100°,则∠ABC等于( )
A. 140° B. 110° C. 120° D. 130°
13. △ABC中,∠C=90°,AB=,BC=,以点A为圆心,以长为半径画圆,则点C在圆A___________,点B在圆A_________;
14. 圆的半径等于,圆内一条弦长2,则弦的中点与弦所对弧的中点的距离等于_____________;
15. 如图所示,已知AB为圆O的直径,AC为弦,OD∥BC交AC于D,OD=,求BC的长;
16. 如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D。已知:AB,CD。(1)求作此残片所在的圆(不写作法,保留作图痕迹);(2)求(1)中所作圆的半径。
在△ABC中,∠C=90°,AC=BC=4cm,D是AB边的中点,以点C为圆心,4cm为半径作圆。则A、B、C、D四点在圆内有_____________。
如图所示,圆O的直径AB和弦CD交于E,已知AE=6cm,EB=2cm,∠CEA=30°,求CD。
第18题 第19题
19. 如图所示,已知O是∠EPF的平分线上的一点,以O为圆心的圆心角的两边分别交于点A、B、C、D求证:PB=PD,若角的顶点P在圆上或圆内,上述还成立吗?请说明。
参考答案1. 过点O作于E
2. 175mm 3. 略 4. 8 5. 6. 7. 3.6 8. 120 9. B
10. D 11. A 12. D13. 内部、外部 14. 15. BC=4cm 16. (2)
17. C、D 18. 19. (1)证明:过O作
(2)上述结论仍成立:
如图所示
图4
图3
同课章节目录
