5.5 一次函数的简单应用（2）

课件25张PPT。义务教育教科书　
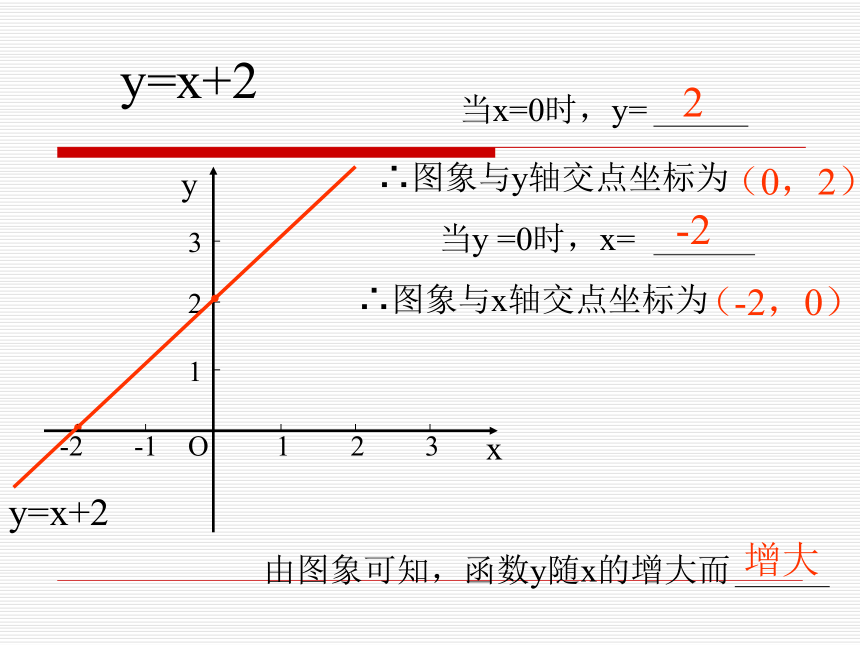
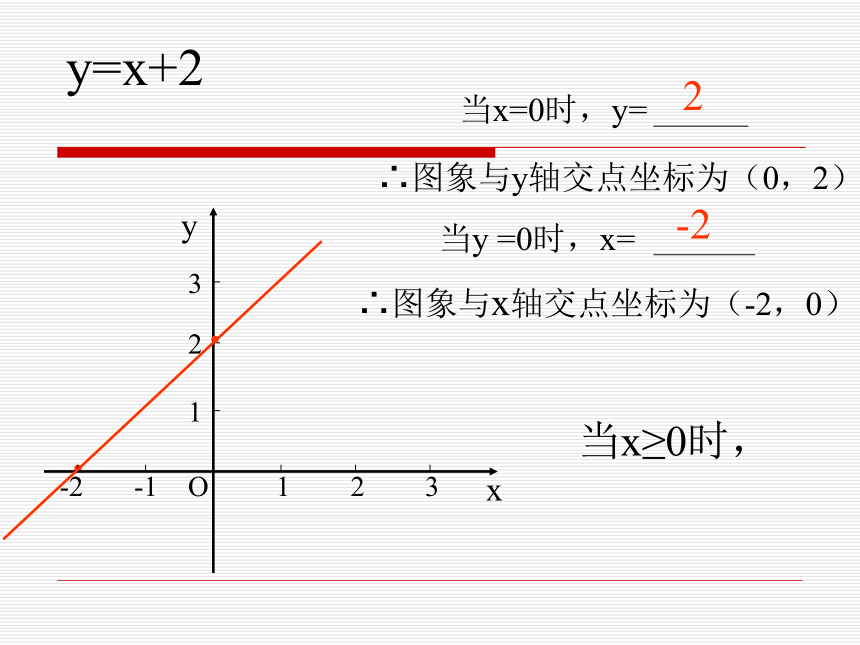
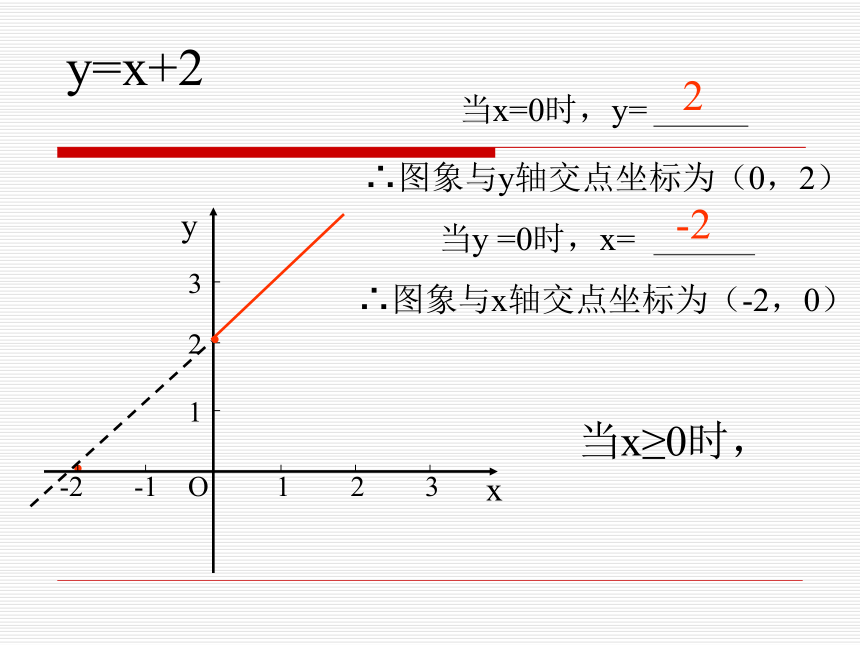
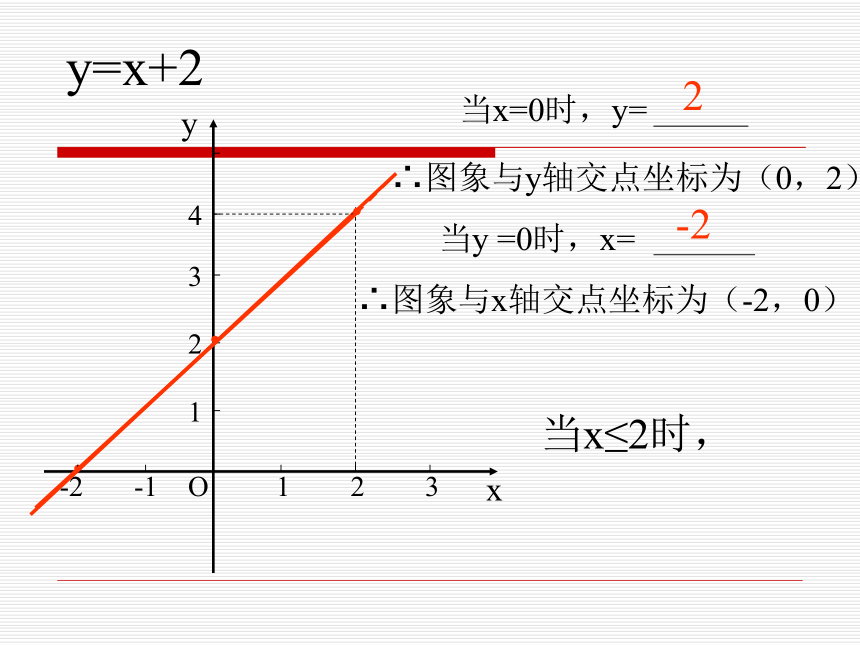
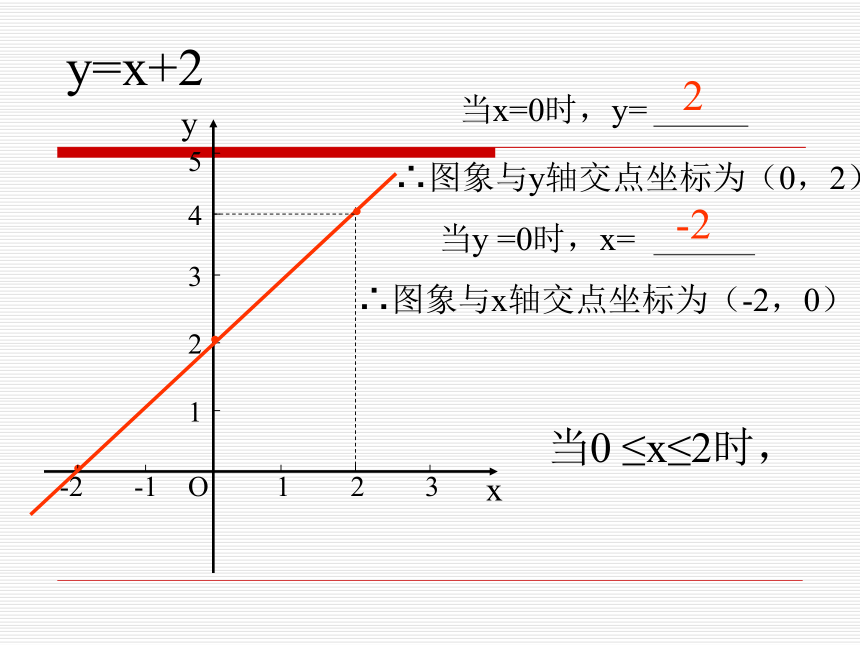
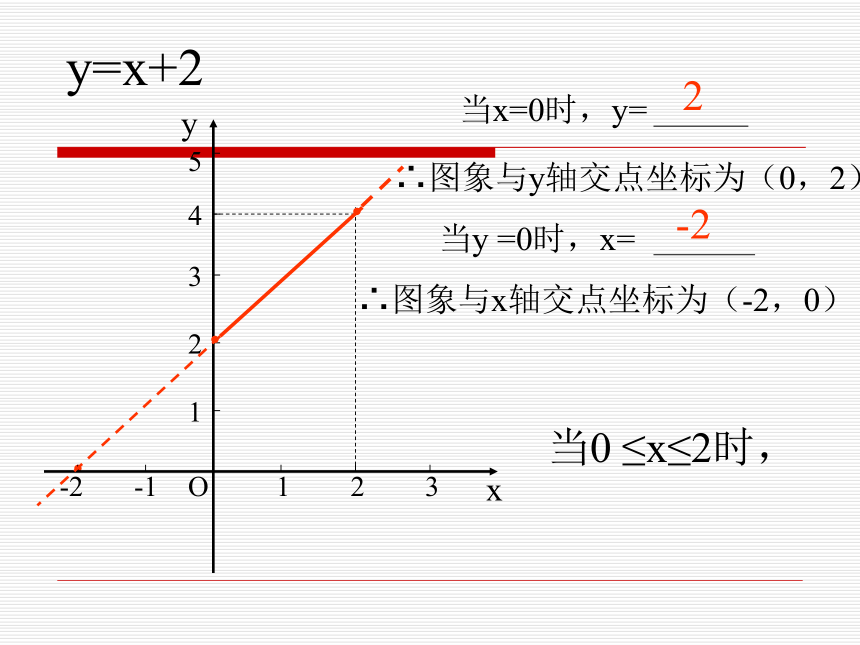
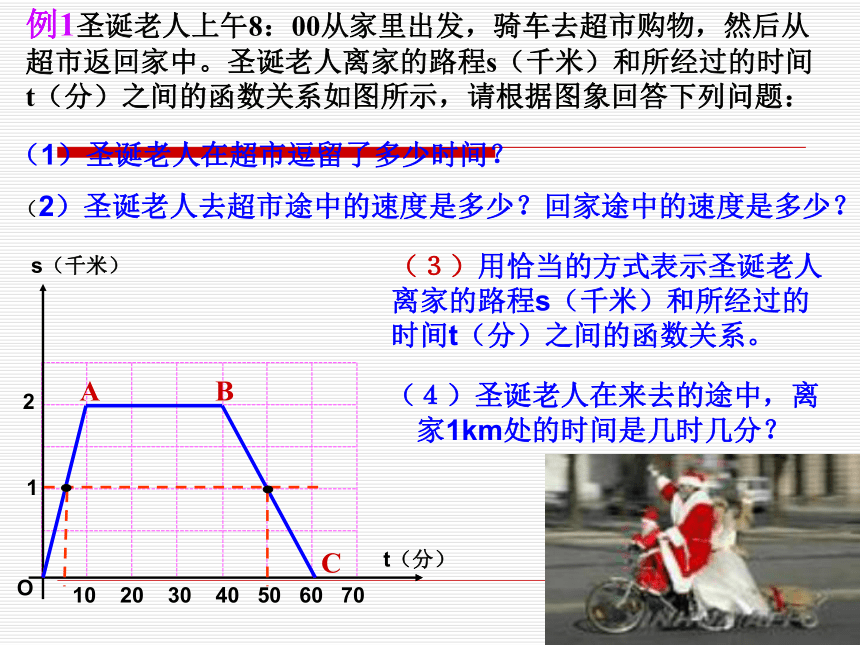
浙教版《数学》八年级上册 5.5 一次函数的简单应用（2）y=x+2··∴图象与y轴交点坐标为∴图象与x轴交点坐标为2-2增大（0，2）（-2，0）y=x+2··∴图象与y轴交点坐标为（0，2）∴图象与x轴交点坐标为（-2，0）当x≥0时，2-2y=x+2··∴图象与y轴交点坐标为（0，2）∴图象与x轴交点坐标为（-2，0）当x≥0时，2-2y=x+2·xyO123123-1-2·∴图象与y轴交点坐标为（0，2）∴图象与x轴交点坐标为（-2，0）当x≤2时，2-24·y=x+2·xyO123123-1-2·∴图象与y轴交点坐标为（0，2）∴图象与x轴交点坐标为（-2，0）当0 ≤x≤2时，2-245·y=x+2·xyO123123-1-2·∴图象与y轴交点坐标为（0，2）∴图象与x轴交点坐标为（-2，0）当0 ≤x≤2时，2-245·（2）圣诞老人去超市途中的速度是多少？回家途中的速度是多少？（1）圣诞老人在超市逗留了多少时间？
（４）圣诞老人在来去的途中，离家1km处的时间是几时几分？（３）用恰当的方式表示圣诞老人离家的路程s（千米）和所经过的时间t（分）之间的函数关系。例1圣诞老人上午8：00从家里出发，骑车去超市购物，然后从超市返回家中。圣诞老人离家的路程s（千米）和所经过的时间t（分）之间的函数关系如图所示，请根据图象回答下列问题：如图，L 反映了某商场圣诞礼品的销售收入与销售量的关系，L 反映了该商场圣诞礼品的销售成本与销售量的关系，根据图意填空：
（1）当销售量为200份时，销售收入＝　　　　元，
　　　销售成本＝　　　　元；20003000（2）当销售量为600份时，销售收入＝　　　　元，
　　　销售成本＝　　　　元；60005000（3）当销售量为　　 时，销售收入等于销售成本；400份（L 1反映销售收入与销售量的关系，L2 反映了销售成本与销售量的关系）（4）当销售量　　　　 时，该商场赢利（收入大于成本）
　　当销售量　　　　 时，该商场亏损（收入小于成本）X＞400X＜400（5） L1对应的函数表达式是　　　　　　　　，
　　 L2对应的函数表达式是　　　　　　　　。y1=10xy2=5x+2000L 1 反映销售收入
与销售量的关系 L 2 反映了销售成本
与销售量的关系 东阳市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若居民应交水费y(元)与用水量x(吨)的函数关系如图所示.(1):分别写出0≤x≤15和x>15时,y与x的函数关系式;
(2):若某用户该月用水21吨,则应交水费多少元?典型例题分析解题思路：关键是识别自变量在不同的取值范围内所对应函数的类型用待定系数法分别求出不同范围内的函数解析式分段函数例2、清华大学登山队某队员在攀登念青唐古拉中央峰时，其距离地面的海拔高度s（米）与时间t（小时）之间的函数关系如图所示。(假设往返均为匀速运动)
（1）你能分别求出0≤t≤12和t＞12时s与t的函数关系式吗?
（2）一般情况下，人到达海拔3000米左右地区时,就开始出现呼吸频率和心率加快、疲乏、头痛等不良症状，那么运动员在这次登山运动中出现这种症状大约会持续多久?S (米)t (小时)0121648002400BA84 S1＝400t（ 0≤ t≤12）
S2＝－600t+12000（t＞12） OA所在的直线是什么函数? AB呢?请解答!C如图所示，某地区对某种药品的需求量y1(万件)，供应量y2(万件)与价格x(元／件)分别近似满足下列函数关系式：y1=-x+70，y2=2x－38，需求量为0时，即停止供应．当y1=y2时，该药品的价格称为稳定价格，需求量称为稳定需求量．
(1)求该药品的稳定价格与稳定需求量．
(2)价格在什么范围内，该药品的需求量低于供应量?
(3)由于该地区突发疫情，政府部门决定对药品供应方提供价格补贴来提高供货价格，以利提高供应量．根据调查统计，需将稳定需求量增加6万件，政府应对每件药品提供多少元补贴，才能使供应量等于需求量?链接体会分享学会反思是学习的一种好习惯你学会了什么知识或方法?你
有什么感想?在本节课中（2）用恰当的方式表示费用y与路程s之间的关系。练习：某市出租车计费方法如图所示，请根据图象回答下面的问题：（1）出租车的起步价是多少元？在多少路程内只收起步价？（3）起步价里程走完之后，每行驶1km需多少车费？（4）某外地客人坐出租车游览本市，车费为31元，试求出他乘车的里程。2.一农民带上若干千克自产的土豆进城出售, 为了方便, 他带了一些零钱备用,按市场价售出一些后, 又降价出售, 售出的土豆千克数x与他手中持有的钱数(含备用零钱)y的关系, 如图所示, 结合图象回答下列问题：
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式.
(3)由表达式你能求出降价前每
千克的土豆价格是多少?
(4)降价后他按每千克0.4元将
剩余土豆售完, 这时他手中的钱
(含备用零钱)是26元, 试问
他一共带了多少千克土豆? (1)农民自带的零钱是5元；（2）设降价前的函数解析式为：y=kx+b,经过（30，20）
（0，5）代入解方程组得：
y=0.5x+5(0＜x≤30)(3)降价前每千克的土豆价格是0.5元。（4）∵0.4(a-30)=6, ∴a=45。答：他一共带了45千克土豆我们应当很好地掌握好充分利用图象信息，正确把握好函数类型，从而达到正确解决函数问题的目的。3、某医药研究所开发了一种新药，在试验药效时发现，如果成人按规定剂量服用后，那么服药后2小时血液中含药量最高，达每毫升6微克，（1微克=10-3毫克），接着逐步衰减，10小时时血液中含药量为每毫升3微克，每毫升血液中含药量y（微克）随时间x（小时）的变化如图所示。当成人按规定剂量服用后：
（1）分别求0≤x≤2和x≥2时，y与x之间的函数解析式；
（2）如果每毫升血液中含药量为4微克以 上时，在治疗疾病时是有效的，那么这个有效的时间是多长？S (米)t (小时)0121648002400解:由图象信息可得:

当S1＝3000时,t＝7.5
当S2＝3000时,t＝15
所以运动员出现这种症状大约会持续15-7.5＝7.5个小时。BA843000S1＝400t（ 0≤ t≤12）
S2＝－600t+12000（t＞12）C 4、 如图,在边长为2的正方形ABCD的一边BC上有一点P 从B点开始运动到C点,设BP=x,四边形APDC的面积为y.(1):求y关于x的函数关系式,并写出自变量x的取值范围;(2):当x为何值时,四边形APCD的面积等于3?(3):当P点由B向C运动时,四边形APCD的面积是越来越大,还是越来越小?(4):你能说出函数y的最大值和最小值吗?ABCDP2x2-x5、如图，矩形OABC中，O为直角坐标系的原点，A、C两点的坐标分别为（3，0）、（0，5）。
（1）直接写出B点坐标；
（2）若过点C的直线CD交AB边于点D，且把矩形OABC的周长分为1∶3两部分，求直线CD的解析式；(1).B(3,5)D(2)设D（3，y)
∴3(3+5-y)=8+y ∴y=4 ∴D(3,4)
设直线CD的解析式为：y=kx+b把C（0，5）D（3，4）代入解方程组得：对与实际问题进行:
收集数据；
画出函数的图象；
判断函数的类型；
求出解析式.就是一个建立数学模型的过程.小结：两个重要的知识块：二:建立数学模型解决实际问题一:利用函数图象解决实际问题