3.4.2圆心角 课件(共24张PPT)
文档属性
| 名称 | 3.4.2圆心角 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-01 11:56:37 | ||
图片预览





文档简介
(共24张PPT)
3.4.2圆心角
浙教版 九年级上册
教学目标
教学目标:
掌握”在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个圆心距中有一对量相等,那么它们所对应的其余各对量都相等”这个圆的性质.
重点:关于圆心角,弧,弦,弦心距之间相互关系的性质
难点:圆心角定理的应用
复习回顾
在⊙O中,当圆心角∠AOB ∠A'OB'时,它们所对的弧
和 ,弦AB和A'B'相等.
O
A
B
A'
B'
(A')
(B')
AB=A'B'
点A与点A'重合;
点B与点B'重合;
AB与A'B'重合;
与 重合.
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
新知讲解
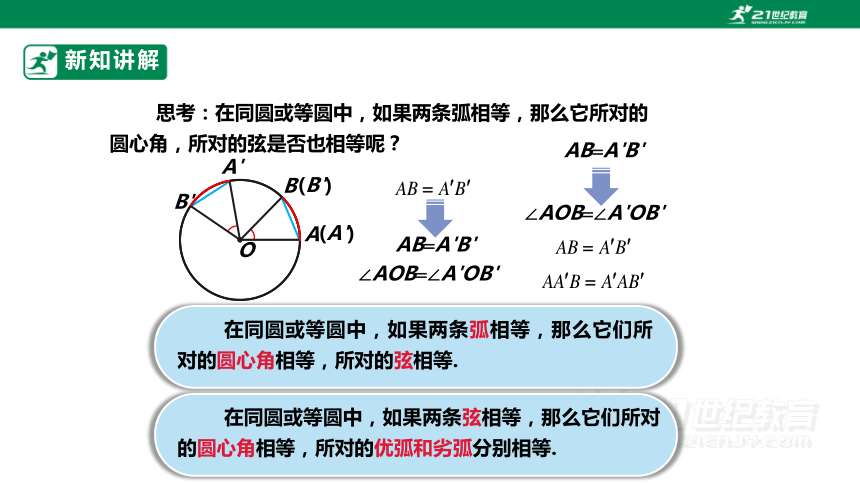
思考:在同圆或等圆中,如果两条弧相等,那么它所对的圆心角,所对的弦是否也相等呢?
O
A
B
A'
B'
(A')
(B')
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等.
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等.
AB A'B'
∠AOB ∠A'OB'
AB A'B'
∠AOB ∠A'OB'
新知讲解
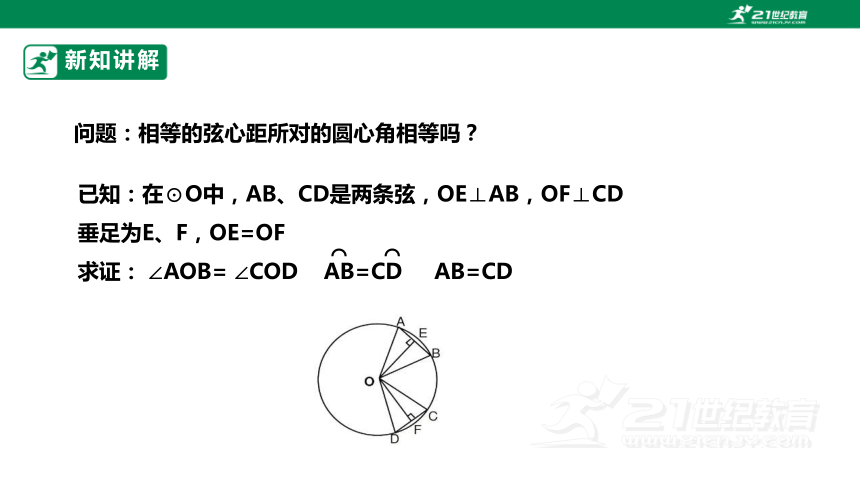
问题:相等的弦心距所对的圆心角相等吗?
已知:在⊙O中,AB、CD是两条弦,OE⊥AB,OF⊥CD
垂足为E、F,OE=OF
求证: ∠AOB= ∠COD AB=CD AB=CD
⌒ ⌒
新知讲解
证明:∵OE⊥AB,OF⊥CD
在Rt △AOE和Rt △COF中
∴ Rt △AOE ≌ Rt △COF
∴ ∠AOE= ∠COF
∵OA=OB OC=OD OE⊥AB,OF⊥CD
∴ ∠ AOB=2∠AOE ∠COD=2∠COF
∴∠AOB= ∠COD
⌒ ⌒
∴AB=CD AB=CD
新知讲解
一般地,圆有下面的性质:
在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等,那么它们所对应的其余的各组量都相等.
B
E
D
A
F
C
O
∠AOB=∠COD
AB=CD
OE=OF
AB=CD
⌒
⌒
⑴ ∠AOB=∠COD
⑵ AB=CD
⑶ OE=OF
⑷ AB=CD
新知讲解
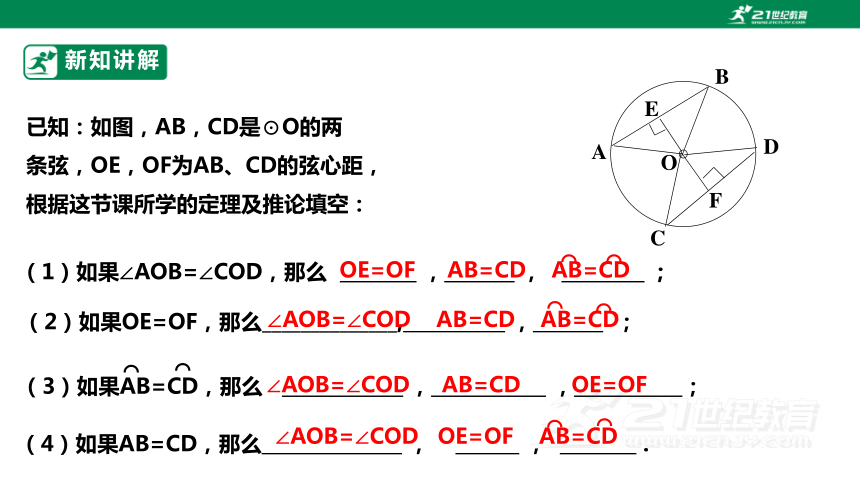
已知:如图,AB,CD是⊙O的两
条弦,OE,OF为AB、CD的弦心距,
根据这节课所学的定理及推论填空:
(2)如果OE=OF,那么______________, , ;
⌒
⌒
(3)如果AB=CD,那么 , , ;
(1)如果∠AOB=∠COD,那么 , , ;
OE=OF AB=CD AB=CD
⌒
⌒
∠AOB=∠COD AB=CD AB=CD
⌒
⌒
∠AOB=∠COD AB=CD OE=OF
∠AOB=∠COD OE=OF AB=CD
⌒
⌒
A
B
C
F
D
E
O
(4)如果AB=CD,那么 , , .
新知讲解
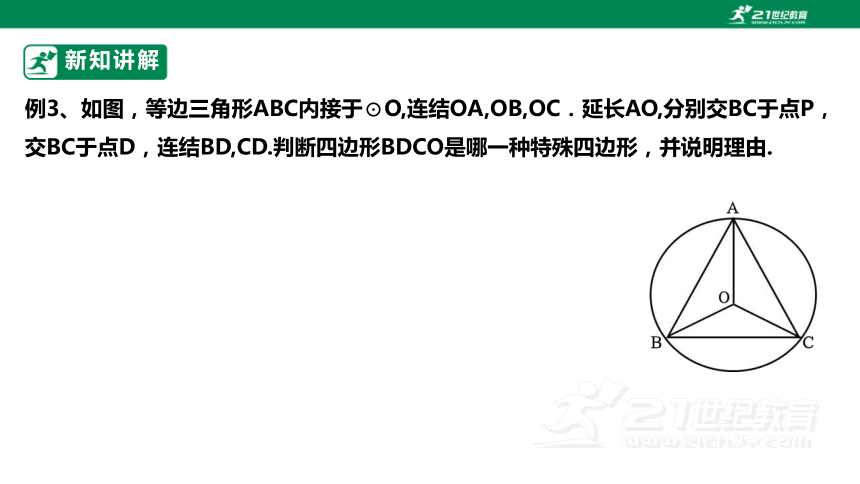
例3、如图,等边三角形ABC内接于⊙O,连结OA,OB,OC.延长AO,分别交BC于点P,交BC于点D,连结BD,CD.判断四边形BDCO是哪一种特殊四边形,并说明理由.
新知讲解
O
C
B
A
D
P
解:四边形BDCO是菱形,理由如下:
∵AB=BC=CA
∴∠AOB=∠BOC=∠COA=120°
∴∠BOD=180°-∠AOB=60°
同理:∠COD=60°
又∵OB=OD
∴OB=OD=BD
同理:OC=CD
∴OB=OC=BD=CD
∴四边形BDCO是菱形
新知讲解
例4、已知:如图, △ABC为等边三角形,以AB为直径的圆O分别交AC,BC于点D,E. 求证:
解: 连结OD,OE
在等边三角形ABC中,∠A=60°
∵OA=OD
∴△AOD为等边三角形
∴∠AOD=60°
同理∠BOE=60°
∴∠DOE= 180°-∠AOD-∠BOE=60°
∴∠DOE= ∠AOD=∠BOE
∴
课堂练习
1. 如图,在⊙O中:
(1)若∠AOC=∠BOC,BC=5,则AC= .
(2)若AC=BC,∠BOC=70°,则∠AOC= .
C
O
A
B
·
5
70°
课堂练习
2.如图,在⊙O中,已知弦AB=DE,OC⊥AB,OF⊥DE,垂足分别为C,F,则下列说法中正确的有( )
①∠DOE=∠AOB;②AB=DE;③OF=OC;④AC=EF
A.1个 B.2个 C.3个 D.4个
(
(
D
课堂练习
3.如图,在⊙O中,已知弦AB=DE,OC⊥AB,OF⊥DE,垂足分别为C,F,则下列说法中正确的有( )
①∠DOE=∠AOB;②AB=DE;③OF=OC;④AC=EF
A.1个 B.2个 C.3个 D.4个
(
(
D
课堂练习
解:
∵BC=CD=DE
4.如图,AB是⊙O 的直径,BC=CD=DE.∠COD=35°,求∠AOE 的度数.
·
A
O
B
C
D
E
⌒
⌒
⌒
⌒
⌒
⌒
课堂练习
5.如图,已知AB、CD为⊙O的两条弦,AD=BC
求证:AB=CD.
.
C
A
B
D
O
(
(
∵AD=BC
(
(
课堂练习
6. 如图,在⊙O中,弦AC,BD相交于点P,且AB CD,
求证:AC BD.
解:∵AB CD,
∴
又∵ ,
∴
∴ AC BD
A
O
B
C
·
D
P
课堂练习
7.如图,已知BD,CE是☉O的两条弦,OA平分∠DAE.求证:AB=AC.
分析:作OM⊥BD于M,ON⊥CE于N,根据角平分线的性质得到OM=ON,根据圆心角、弧、弦之间的关系得到BD=CE,证明△AMO≌△ANO,得到AM=AN,得到答案.
课堂练习
证明:作OM⊥BD于M,ON⊥CE于N,
∵OA平分∠DAE,∴OM=ON,∴BD=CE.
∵OM⊥BD,ON⊥CE,
∴△AMO≌△ANO,∴AM=AN,∴AB=AC.
课堂练习
8.如图,已知点O是∠EPF 的平分线上一点,P点在圆外,以O为圆心的圆与∠EPF 的两边分别相交于A、B和C、D.
求证:AB=CD
分析: 联想到“角平分线的性质”,作弦心距OM、ON,
要证AB=CD ,只需证OM=ON.
.
P
A
B
E
C
D
F
O
课堂练习
.
M
N
P
A
B
E
C
D
F
O
课堂小结
在同圆或等圆中,如果 ①两个圆心角,②两条弧,③两条弦,
④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.4.2圆心角
浙教版 九年级上册
教学目标
教学目标:
掌握”在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个圆心距中有一对量相等,那么它们所对应的其余各对量都相等”这个圆的性质.
重点:关于圆心角,弧,弦,弦心距之间相互关系的性质
难点:圆心角定理的应用
复习回顾
在⊙O中,当圆心角∠AOB ∠A'OB'时,它们所对的弧
和 ,弦AB和A'B'相等.
O
A
B
A'
B'
(A')
(B')
AB=A'B'
点A与点A'重合;
点B与点B'重合;
AB与A'B'重合;
与 重合.
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
新知讲解
思考:在同圆或等圆中,如果两条弧相等,那么它所对的圆心角,所对的弦是否也相等呢?
O
A
B
A'
B'
(A')
(B')
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等.
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等.
AB A'B'
∠AOB ∠A'OB'
AB A'B'
∠AOB ∠A'OB'
新知讲解
问题:相等的弦心距所对的圆心角相等吗?
已知:在⊙O中,AB、CD是两条弦,OE⊥AB,OF⊥CD
垂足为E、F,OE=OF
求证: ∠AOB= ∠COD AB=CD AB=CD
⌒ ⌒
新知讲解
证明:∵OE⊥AB,OF⊥CD
在Rt △AOE和Rt △COF中
∴ Rt △AOE ≌ Rt △COF
∴ ∠AOE= ∠COF
∵OA=OB OC=OD OE⊥AB,OF⊥CD
∴ ∠ AOB=2∠AOE ∠COD=2∠COF
∴∠AOB= ∠COD
⌒ ⌒
∴AB=CD AB=CD
新知讲解
一般地,圆有下面的性质:
在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等,那么它们所对应的其余的各组量都相等.
B
E
D
A
F
C
O
∠AOB=∠COD
AB=CD
OE=OF
AB=CD
⌒
⌒
⑴ ∠AOB=∠COD
⑵ AB=CD
⑶ OE=OF
⑷ AB=CD
新知讲解
已知:如图,AB,CD是⊙O的两
条弦,OE,OF为AB、CD的弦心距,
根据这节课所学的定理及推论填空:
(2)如果OE=OF,那么______________, , ;
⌒
⌒
(3)如果AB=CD,那么 , , ;
(1)如果∠AOB=∠COD,那么 , , ;
OE=OF AB=CD AB=CD
⌒
⌒
∠AOB=∠COD AB=CD AB=CD
⌒
⌒
∠AOB=∠COD AB=CD OE=OF
∠AOB=∠COD OE=OF AB=CD
⌒
⌒
A
B
C
F
D
E
O
(4)如果AB=CD,那么 , , .
新知讲解
例3、如图,等边三角形ABC内接于⊙O,连结OA,OB,OC.延长AO,分别交BC于点P,交BC于点D,连结BD,CD.判断四边形BDCO是哪一种特殊四边形,并说明理由.
新知讲解
O
C
B
A
D
P
解:四边形BDCO是菱形,理由如下:
∵AB=BC=CA
∴∠AOB=∠BOC=∠COA=120°
∴∠BOD=180°-∠AOB=60°
同理:∠COD=60°
又∵OB=OD
∴OB=OD=BD
同理:OC=CD
∴OB=OC=BD=CD
∴四边形BDCO是菱形
新知讲解
例4、已知:如图, △ABC为等边三角形,以AB为直径的圆O分别交AC,BC于点D,E. 求证:
解: 连结OD,OE
在等边三角形ABC中,∠A=60°
∵OA=OD
∴△AOD为等边三角形
∴∠AOD=60°
同理∠BOE=60°
∴∠DOE= 180°-∠AOD-∠BOE=60°
∴∠DOE= ∠AOD=∠BOE
∴
课堂练习
1. 如图,在⊙O中:
(1)若∠AOC=∠BOC,BC=5,则AC= .
(2)若AC=BC,∠BOC=70°,则∠AOC= .
C
O
A
B
·
5
70°
课堂练习
2.如图,在⊙O中,已知弦AB=DE,OC⊥AB,OF⊥DE,垂足分别为C,F,则下列说法中正确的有( )
①∠DOE=∠AOB;②AB=DE;③OF=OC;④AC=EF
A.1个 B.2个 C.3个 D.4个
(
(
D
课堂练习
3.如图,在⊙O中,已知弦AB=DE,OC⊥AB,OF⊥DE,垂足分别为C,F,则下列说法中正确的有( )
①∠DOE=∠AOB;②AB=DE;③OF=OC;④AC=EF
A.1个 B.2个 C.3个 D.4个
(
(
D
课堂练习
解:
∵BC=CD=DE
4.如图,AB是⊙O 的直径,BC=CD=DE.∠COD=35°,求∠AOE 的度数.
·
A
O
B
C
D
E
⌒
⌒
⌒
⌒
⌒
⌒
课堂练习
5.如图,已知AB、CD为⊙O的两条弦,AD=BC
求证:AB=CD.
.
C
A
B
D
O
(
(
∵AD=BC
(
(
课堂练习
6. 如图,在⊙O中,弦AC,BD相交于点P,且AB CD,
求证:AC BD.
解:∵AB CD,
∴
又∵ ,
∴
∴ AC BD
A
O
B
C
·
D
P
课堂练习
7.如图,已知BD,CE是☉O的两条弦,OA平分∠DAE.求证:AB=AC.
分析:作OM⊥BD于M,ON⊥CE于N,根据角平分线的性质得到OM=ON,根据圆心角、弧、弦之间的关系得到BD=CE,证明△AMO≌△ANO,得到AM=AN,得到答案.
课堂练习
证明:作OM⊥BD于M,ON⊥CE于N,
∵OA平分∠DAE,∴OM=ON,∴BD=CE.
∵OM⊥BD,ON⊥CE,
∴△AMO≌△ANO,∴AM=AN,∴AB=AC.
课堂练习
8.如图,已知点O是∠EPF 的平分线上一点,P点在圆外,以O为圆心的圆与∠EPF 的两边分别相交于A、B和C、D.
求证:AB=CD
分析: 联想到“角平分线的性质”,作弦心距OM、ON,
要证AB=CD ,只需证OM=ON.
.
P
A
B
E
C
D
F
O
课堂练习
.
M
N
P
A
B
E
C
D
F
O
课堂小结
在同圆或等圆中,如果 ①两个圆心角,②两条弧,③两条弦,
④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
