4.2由平行线截得的比例线段 课件(共24张PPT)
文档属性
| 名称 | 4.2由平行线截得的比例线段 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 17:41:47 | ||
图片预览






文档简介
(共24张PPT)
4.2由平行线截得的比例线段
浙教版 九年级上册
教学目标
教学目标:
1.了解平行线分线段成比例定理.
2.会用平行线分线段成比例定理解决实际问题.
重点:平行线分线段成比例定理及其推论.
难点:灵活运用平行线分线段成比例定理及其推论解决有关问题.
情景导入
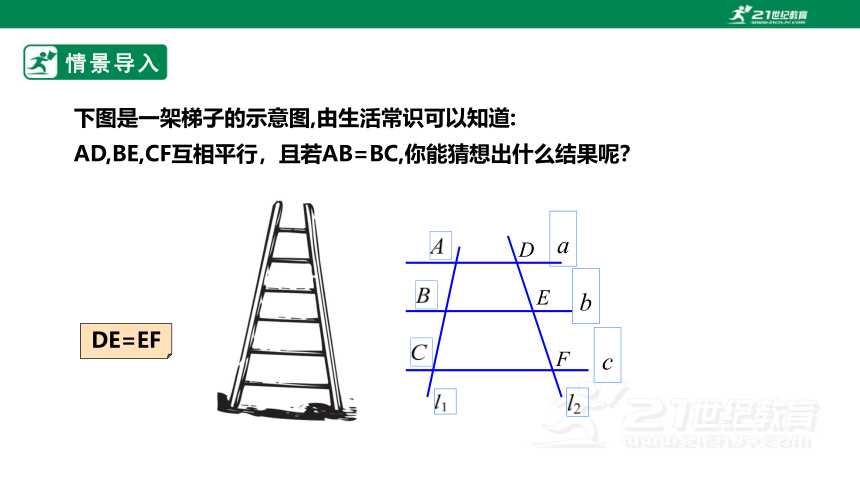
下图是一架梯子的示意图,由生活常识可以知道:
AD,BE,CF互相平行,且若AB=BC,你能猜想出什么结果呢?
a
b
c
DE=EF
D
F
E
合作探究
1.观察有横格线的练习簿页(如图),这些横格线有什么特征 在图中任意画几条直线,使之与横格线相交.这些横格线在每一条所画的直线上截得的线段有什么规律
合作探究
2.观察下图. l1,l2,l3, l4,l5是一组等距离的平行线.
AE与A'E'是任意画的两条直线,分别与这组平行线依次相交于点A,B,C,D,E和A',B',C',D',E'.
比例式=成立吗 = 呢? = 呢?
为什么?你还能再找出两组比例线段吗
新知讲解
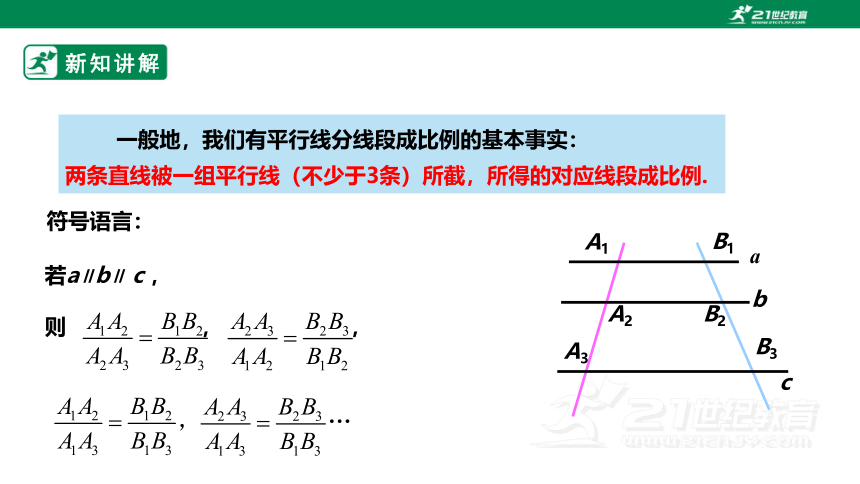
一般地,我们有平行线分线段成比例的基本事实:
两条直线被一组平行线(不少于3条)所截,所得的对应线段成比例.
符号语言:
若a∥b∥ c ,则 , ,
A1
A2
A3
B1
B2
B3
b
c
a
新知讲解
平行线分线段成比例定理的推论
思考:如图,直线a∥b∥ c,由平行线分线段成比例的基本事实,我们可以得出图中对应成比例的线段,
A1
A2
A3
B1
B2
B3
b
c
m
n
a
把直线 n 向左或向右任意平移,这些线段依然成比例.
新知讲解
A1
A2
A3
b
c
m
B1
B2
B3
n
a
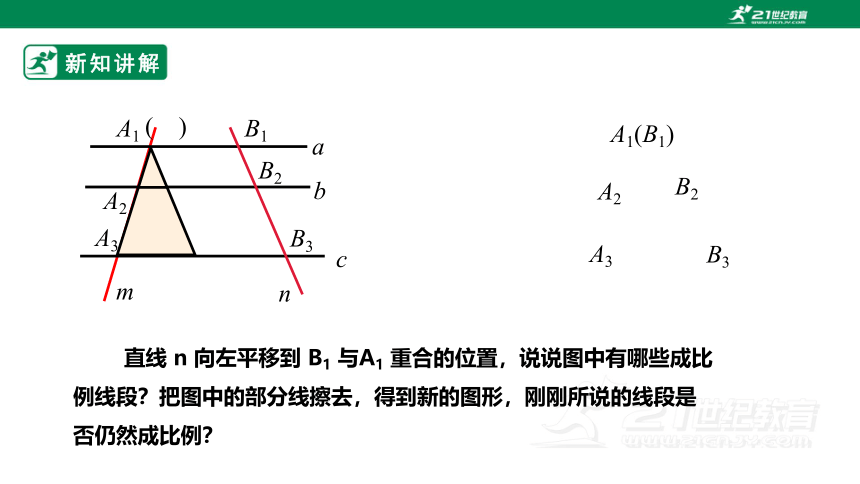
直线 n 向左平移到 B1 与A1 重合的位置,说说图中有哪些成比例线段?把图中的部分线擦去,得到新的图形,刚刚所说的线段是否仍然成比例?
A1(B1)
A2
A3
B2
B3
( )
新知讲解
直线 n 向左平移到 B2 与A2 重合的位置,说说图中有哪些成比例线段?把图中的部分线擦去,得到新的图形,刚刚所说的线段是否仍然成比例?
A1
A2
A3
b
c
m
B1
B2
B3
n
a
A2(B2)
A1
A3
B1
B3
( )
新知讲解
A1(B1)
A2
A3
B2
B3
A2(B2)
A1
A3
B1
B3
归纳
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
新知讲解
例1 如图,直线l1 // l2 // l3 ,直线AC分别交l1, l2, l3 于点A,B,C;直线DF分别交l1, l2, l3 于点D,E,F;已知DE=3,EF=6,AB=4,求AC的长.
A
B
C
D
E
F
l1
l2
l3
解:////
∴(两条直线被一组平行线所截, 所得的对应线段成比例)
∴
∴AC=12
新知讲解
例2、已知线段AB,把线段AB五等分.
作法 :如图:
1.以A为端点作一条射线,并在射线上依次截取线段AA1=A1A2=A2A3=A3A4=A4A5.
2. 连结 A5B,并过点A1, A2, A3, A4 分别作 A5B的平行线,依次交AB于点B1, B2, B3, B4. 点B1, B2, B3, B4 就是所求作的把线段AB五等分的点.
新知讲解
事实上,我们只要过点A作一条与A5B平行的直线l(如图),就可以根据“两条直线被一组平行线所截,所得的对应线段成比例”的基本事实,得到:
= = = = .
而AA1=A1A2=A2A3=A3A4=A4A5,
∴AB1=B1B2=B2B3=B3B4=B4B,
这就证明了点B1,B2,B3,B4是所求作的分点.
课堂练习
1.如图,已知l1∥l2∥l3,下列比例式中错误的是 ( )
A. B.
C. D.
D
A
C
E
B
D
F
l2
l1
l3
课堂练习
2.已知:如图,直线l1∥l2∥l3,AB=4,BC=6,DE=3,则EF为( )
A.2 B.4.5 C.6 D.8
B
课堂练习
3.如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若 ,DE=4,则EF的长是( )
C
课堂练习
4.如图,AD是△ABC的中线,AE=EF=FC,BE交AD于G,
则 _____
5.如图,AB∥DC,AC交BD于点O,已知 ,BO=6,则DO=________.
10
课堂练习
6.如图,在△ABC中,点D,E分别是AB和AC上的点,且DE//BC.若AE=1,AD=CE=2,则BD= ,AB= .
4
6
课堂练习
7. 如图,已知菱形 ABCD 内接于△AEF,AE=5cm,AF = 4 cm,求菱形的边长.
解:∵ 四边形 ABCD 为菱形,
B
C
A
D
E
F
∴CD∥AB,
∴
设菱形的边长为 x cm,则CD = AD = x cm,DF = (4-x) cm,
∴ 解得 x = ∴菱形的边长为 cm.
课堂练习
8.如图,AB=AC,AD⊥BC于点D,M是AD的中点, CM交AB于点P,DN ∥CP.
(1)若AB=6cm,求AP的长;
(2)若PM=1cm,求PC的长.
解:(1)∵ AB = AC,AD⊥BC于点D,M是AD的中点,
∴ DB = DC,AM = MD.
∵ DN ∥CP,
又∵AB = 6cm,
∴ AP = 2cm.
课堂练习
(2)若PM = 1cm,求PC的长.
∵DN ∥CP ,
又∵ PM = 1cm,
∴ PC = 2ND = 4PM = 4cm.
解:由(1)知 AP = PN = NB ,
课堂小结
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例
平行线分线段成比例
基本事实
推论
两条直线被一组平行线所截,所得的对应线段成比例
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
4.2由平行线截得的比例线段
浙教版 九年级上册
教学目标
教学目标:
1.了解平行线分线段成比例定理.
2.会用平行线分线段成比例定理解决实际问题.
重点:平行线分线段成比例定理及其推论.
难点:灵活运用平行线分线段成比例定理及其推论解决有关问题.
情景导入
下图是一架梯子的示意图,由生活常识可以知道:
AD,BE,CF互相平行,且若AB=BC,你能猜想出什么结果呢?
a
b
c
DE=EF
D
F
E
合作探究
1.观察有横格线的练习簿页(如图),这些横格线有什么特征 在图中任意画几条直线,使之与横格线相交.这些横格线在每一条所画的直线上截得的线段有什么规律
合作探究
2.观察下图. l1,l2,l3, l4,l5是一组等距离的平行线.
AE与A'E'是任意画的两条直线,分别与这组平行线依次相交于点A,B,C,D,E和A',B',C',D',E'.
比例式=成立吗 = 呢? = 呢?
为什么?你还能再找出两组比例线段吗
新知讲解
一般地,我们有平行线分线段成比例的基本事实:
两条直线被一组平行线(不少于3条)所截,所得的对应线段成比例.
符号语言:
若a∥b∥ c ,则 , ,
A1
A2
A3
B1
B2
B3
b
c
a
新知讲解
平行线分线段成比例定理的推论
思考:如图,直线a∥b∥ c,由平行线分线段成比例的基本事实,我们可以得出图中对应成比例的线段,
A1
A2
A3
B1
B2
B3
b
c
m
n
a
把直线 n 向左或向右任意平移,这些线段依然成比例.
新知讲解
A1
A2
A3
b
c
m
B1
B2
B3
n
a
直线 n 向左平移到 B1 与A1 重合的位置,说说图中有哪些成比例线段?把图中的部分线擦去,得到新的图形,刚刚所说的线段是否仍然成比例?
A1(B1)
A2
A3
B2
B3
( )
新知讲解
直线 n 向左平移到 B2 与A2 重合的位置,说说图中有哪些成比例线段?把图中的部分线擦去,得到新的图形,刚刚所说的线段是否仍然成比例?
A1
A2
A3
b
c
m
B1
B2
B3
n
a
A2(B2)
A1
A3
B1
B3
( )
新知讲解
A1(B1)
A2
A3
B2
B3
A2(B2)
A1
A3
B1
B3
归纳
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
新知讲解
例1 如图,直线l1 // l2 // l3 ,直线AC分别交l1, l2, l3 于点A,B,C;直线DF分别交l1, l2, l3 于点D,E,F;已知DE=3,EF=6,AB=4,求AC的长.
A
B
C
D
E
F
l1
l2
l3
解:////
∴(两条直线被一组平行线所截, 所得的对应线段成比例)
∴
∴AC=12
新知讲解
例2、已知线段AB,把线段AB五等分.
作法 :如图:
1.以A为端点作一条射线,并在射线上依次截取线段AA1=A1A2=A2A3=A3A4=A4A5.
2. 连结 A5B,并过点A1, A2, A3, A4 分别作 A5B的平行线,依次交AB于点B1, B2, B3, B4. 点B1, B2, B3, B4 就是所求作的把线段AB五等分的点.
新知讲解
事实上,我们只要过点A作一条与A5B平行的直线l(如图),就可以根据“两条直线被一组平行线所截,所得的对应线段成比例”的基本事实,得到:
= = = = .
而AA1=A1A2=A2A3=A3A4=A4A5,
∴AB1=B1B2=B2B3=B3B4=B4B,
这就证明了点B1,B2,B3,B4是所求作的分点.
课堂练习
1.如图,已知l1∥l2∥l3,下列比例式中错误的是 ( )
A. B.
C. D.
D
A
C
E
B
D
F
l2
l1
l3
课堂练习
2.已知:如图,直线l1∥l2∥l3,AB=4,BC=6,DE=3,则EF为( )
A.2 B.4.5 C.6 D.8
B
课堂练习
3.如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若 ,DE=4,则EF的长是( )
C
课堂练习
4.如图,AD是△ABC的中线,AE=EF=FC,BE交AD于G,
则 _____
5.如图,AB∥DC,AC交BD于点O,已知 ,BO=6,则DO=________.
10
课堂练习
6.如图,在△ABC中,点D,E分别是AB和AC上的点,且DE//BC.若AE=1,AD=CE=2,则BD= ,AB= .
4
6
课堂练习
7. 如图,已知菱形 ABCD 内接于△AEF,AE=5cm,AF = 4 cm,求菱形的边长.
解:∵ 四边形 ABCD 为菱形,
B
C
A
D
E
F
∴CD∥AB,
∴
设菱形的边长为 x cm,则CD = AD = x cm,DF = (4-x) cm,
∴ 解得 x = ∴菱形的边长为 cm.
课堂练习
8.如图,AB=AC,AD⊥BC于点D,M是AD的中点, CM交AB于点P,DN ∥CP.
(1)若AB=6cm,求AP的长;
(2)若PM=1cm,求PC的长.
解:(1)∵ AB = AC,AD⊥BC于点D,M是AD的中点,
∴ DB = DC,AM = MD.
∵ DN ∥CP,
又∵AB = 6cm,
∴ AP = 2cm.
课堂练习
(2)若PM = 1cm,求PC的长.
∵DN ∥CP ,
又∵ PM = 1cm,
∴ PC = 2ND = 4PM = 4cm.
解:由(1)知 AP = PN = NB ,
课堂小结
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例
平行线分线段成比例
基本事实
推论
两条直线被一组平行线所截,所得的对应线段成比例
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
