浙教版数学八年级上册2.3等腰三角形的性质定理 第1课时 课件(共18张PPT)
文档属性
| 名称 | 浙教版数学八年级上册2.3等腰三角形的性质定理 第1课时 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 188.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
2.3 等腰三角形的性质定理(一)
浙教版《数学》八年级上册
教学目标
1.经历等腰三角形性质的推导过程,加深轴对称变换的认识;
2.掌握等腰三角形的性质,并能进行简单的推理、判断、计算、和作图.
经历探索新知的过程,体验数学推理的必要性.
通过观察、归纳等活动,培养学生的逻辑推理能力.
知识目标
能力目标
情感目标
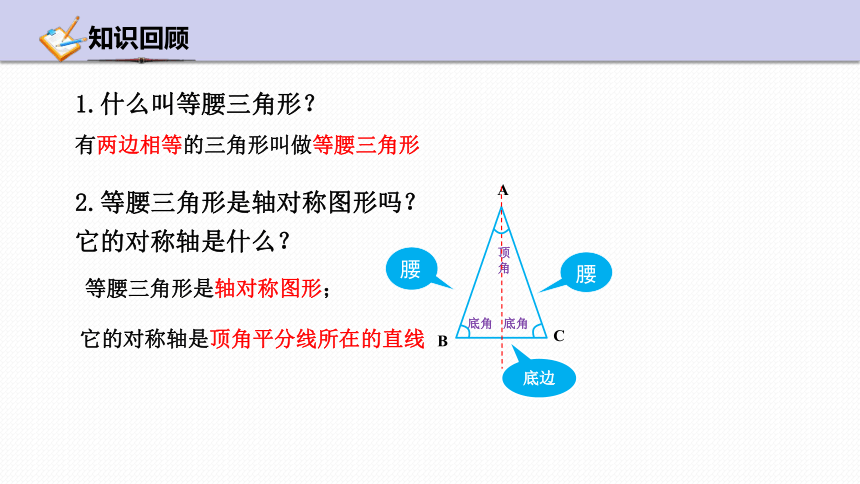
1.什么叫等腰三角形?
2.等腰三角形是轴对称图形吗?
它的对称轴是什么?
腰
腰
底边
A
C
B
顶
角
底角 底角
有两边相等的三角形叫做等腰三角形
等腰三角形是轴对称图形;
它的对称轴是顶角平分线所在的直线
知识回顾
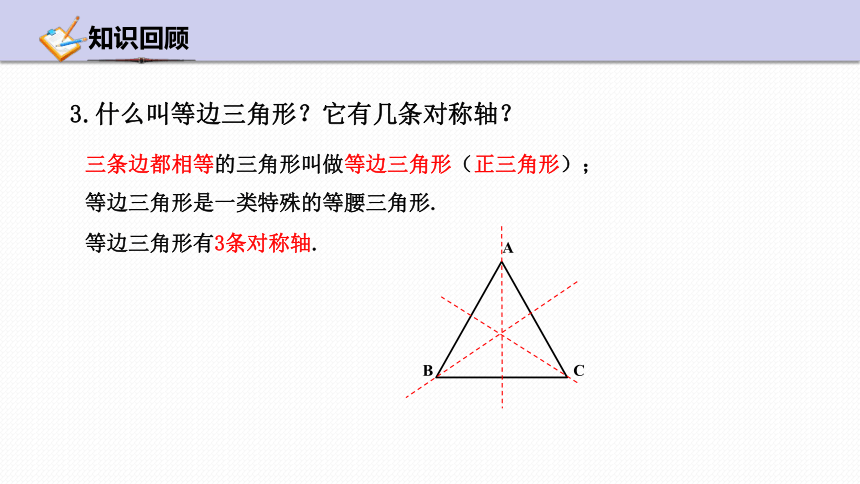
3.什么叫等边三角形?它有几条对称轴?
A
C
B
三条边都相等的三角形叫做等边三角形(正三角形);
等边三角形是一类特殊的等腰三角形.
等边三角形有3条对称轴.
知识回顾
请任意画一个等腰三角形,通过折叠、测量等方式,探索它的内角之间有什么关系?
你发现了什么
B
A
C
(B)
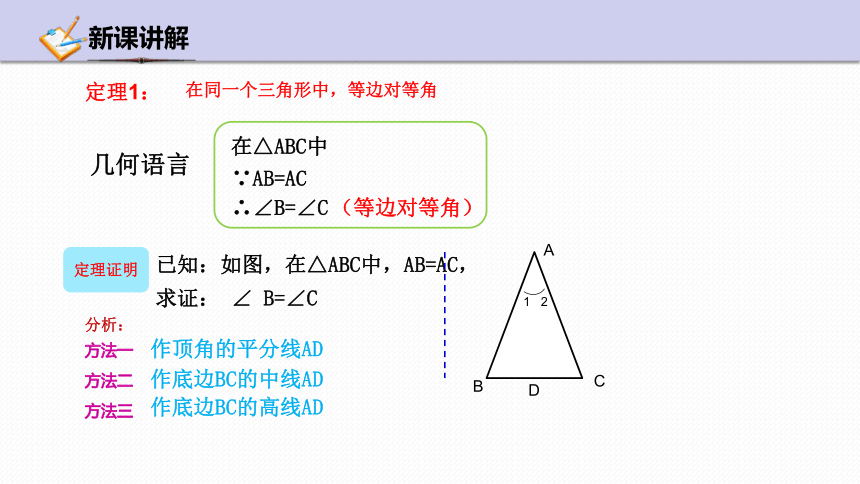
等腰三角形的性质定理1:
等腰三角形的两个底角相等.
在同一个三角形中,
等边对等角
这个定理也可以说成
等边对等角
简写成
B
新课引入
已知:如图,在△ABC中,AB=AC,
求证: ∠ B=∠C
在同一个三角形中,等边对等角
方法一
分析:
作顶角的平分线AD
方法二
作底边BC的中线AD
方法三
作底边BC的高线AD
A
B
C
D
1 2
∵AB=AC
∴∠B=∠C
(等边对等角)
在△ABC中
定理1:
定理证明
新课讲解
几何语言
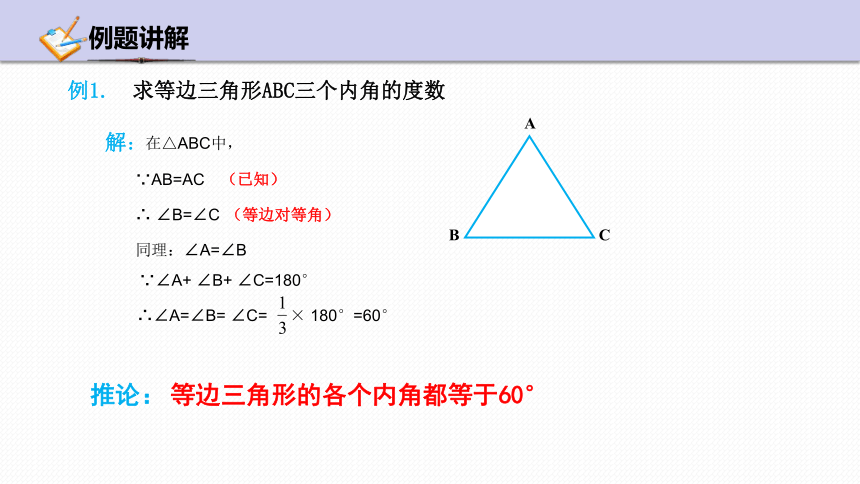
例1. 求等边三角形ABC三个内角的度数
A
C
B
等边三角形的各个内角都等于60°
解:
在△ABC中,
∵AB=AC
(已知)
∴ ∠B=∠C
(等边对等角)
同理:∠A=∠B
∵∠A+ ∠B+ ∠C=180°
∴∠A=∠B= ∠C= × 180°=60°
推论:
例题讲解
例2 求证:等腰三角形两底角的平分线相等.
已知:如图,在△ABC中,AB=AC,BD与CE
是△ABC的两条角平分线.
A
B
C
D
E
分析思路:
BD=CE
△BCE≌△CBD
BC=CB(已知)
BD,CE是△ABC的角平分线(已知)
AB=AC(已知)
∠ABC=∠ACB
∠BCE=∠CBD
求证:BD=CE
分析法
例题讲解
分析法又叫逆推法,是从分析每一个结论的必要条件开始,步步倒推,直至说明题目给出的条件恰好符合要求为止.
实际是把证明反过来了,但又并不完全一样.
拓展延伸
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
等腰三角形两腰上的中线相等.
等腰三角形两腰上的高线相等.
等腰三角形两底角的角平分线相等.
合作学习
1.如图,在△ABC中,AB=AC,∠A=50°,
求∠B ,∠C的度数.
解:
∵AB=AC
∴ ∠B =∠C
(等边对等角)
∵∠A+∠B+∠C=180°
∠A=50°
∴∠B+∠C=130°
∴∠B=∠C=65°
做一做
A
B
C
已知:在等腰△ABC中, ∠ B =80°,
求:∠C和∠A的度数
∠B所在位置可能有几种?
底角或顶角
分析:
(1)当∠B为底角时,
(2)当∠B为顶角时,
或∠A为80°,∠C为20°.
∠C为80°, ∠A为20°
∠C为50°, ∠A为50°.
思考:
A
B
C
A
B
C
A
B
C
温馨提示
等腰三角形中的内角,若没指出是底角还是顶角,应该分成两种情况讨论,然后运用三角形的内角和为180°求解.
做一做
1.等腰三角形的一个底角为70°,它的顶角为 .
2.等腰三角形的一个角为70°,它的顶角为 .
3.等腰三角形的一个角为70°,它的另外两个角为 .
4.等腰三角形的一个内角的外角为100°,它的顶角为 .
40°
40°或70°
40°,70°或55°,55°
80°或20°
练一练
5.等腰三角形的一个内角的外角为80°,它的顶角为 .
6.等腰三角形一腰上的高与底边的夹角为40°,则顶角为 .
7.等腰三角形一腰上的高与另一腰的夹角为40°,则顶角为 .
80°
50°或130°
100°
练一练
8.如图,在△ABC中,D在AC上,且BD=BC=AD,求△ABC各内角的度数?
练一练
A
B
C
D
9.如图,在△ABC中,点D、E在△ABC的边BC上,且AB=AC,AD=AE,此时BD与CE有什么关系?请说明理由.(至少两种方法证明)
一展身手
A
B
C
D
E
10.已知,如图,AB=BC=CD=ED=EF. ∠A=15°,试求∠FEM的度数?
一展身手
M
N
A
B
C
D
E
F
11.如图,钢架中A=16°,焊上等长的钢条BC,CD,DE…来加固钢架,若AB=BC,则这样的钢条至多需要多少根?
一展身手
A
B
C
D
E
再见
2.3 等腰三角形的性质定理(一)
浙教版《数学》八年级上册
教学目标
1.经历等腰三角形性质的推导过程,加深轴对称变换的认识;
2.掌握等腰三角形的性质,并能进行简单的推理、判断、计算、和作图.
经历探索新知的过程,体验数学推理的必要性.
通过观察、归纳等活动,培养学生的逻辑推理能力.
知识目标
能力目标
情感目标
1.什么叫等腰三角形?
2.等腰三角形是轴对称图形吗?
它的对称轴是什么?
腰
腰
底边
A
C
B
顶
角
底角 底角
有两边相等的三角形叫做等腰三角形
等腰三角形是轴对称图形;
它的对称轴是顶角平分线所在的直线
知识回顾
3.什么叫等边三角形?它有几条对称轴?
A
C
B
三条边都相等的三角形叫做等边三角形(正三角形);
等边三角形是一类特殊的等腰三角形.
等边三角形有3条对称轴.
知识回顾
请任意画一个等腰三角形,通过折叠、测量等方式,探索它的内角之间有什么关系?
你发现了什么
B
A
C
(B)
等腰三角形的性质定理1:
等腰三角形的两个底角相等.
在同一个三角形中,
等边对等角
这个定理也可以说成
等边对等角
简写成
B
新课引入
已知:如图,在△ABC中,AB=AC,
求证: ∠ B=∠C
在同一个三角形中,等边对等角
方法一
分析:
作顶角的平分线AD
方法二
作底边BC的中线AD
方法三
作底边BC的高线AD
A
B
C
D
1 2
∵AB=AC
∴∠B=∠C
(等边对等角)
在△ABC中
定理1:
定理证明
新课讲解
几何语言
例1. 求等边三角形ABC三个内角的度数
A
C
B
等边三角形的各个内角都等于60°
解:
在△ABC中,
∵AB=AC
(已知)
∴ ∠B=∠C
(等边对等角)
同理:∠A=∠B
∵∠A+ ∠B+ ∠C=180°
∴∠A=∠B= ∠C= × 180°=60°
推论:
例题讲解
例2 求证:等腰三角形两底角的平分线相等.
已知:如图,在△ABC中,AB=AC,BD与CE
是△ABC的两条角平分线.
A
B
C
D
E
分析思路:
BD=CE
△BCE≌△CBD
BC=CB(已知)
BD,CE是△ABC的角平分线(已知)
AB=AC(已知)
∠ABC=∠ACB
∠BCE=∠CBD
求证:BD=CE
分析法
例题讲解
分析法又叫逆推法,是从分析每一个结论的必要条件开始,步步倒推,直至说明题目给出的条件恰好符合要求为止.
实际是把证明反过来了,但又并不完全一样.
拓展延伸
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
等腰三角形两腰上的中线相等.
等腰三角形两腰上的高线相等.
等腰三角形两底角的角平分线相等.
合作学习
1.如图,在△ABC中,AB=AC,∠A=50°,
求∠B ,∠C的度数.
解:
∵AB=AC
∴ ∠B =∠C
(等边对等角)
∵∠A+∠B+∠C=180°
∠A=50°
∴∠B+∠C=130°
∴∠B=∠C=65°
做一做
A
B
C
已知:在等腰△ABC中, ∠ B =80°,
求:∠C和∠A的度数
∠B所在位置可能有几种?
底角或顶角
分析:
(1)当∠B为底角时,
(2)当∠B为顶角时,
或∠A为80°,∠C为20°.
∠C为80°, ∠A为20°
∠C为50°, ∠A为50°.
思考:
A
B
C
A
B
C
A
B
C
温馨提示
等腰三角形中的内角,若没指出是底角还是顶角,应该分成两种情况讨论,然后运用三角形的内角和为180°求解.
做一做
1.等腰三角形的一个底角为70°,它的顶角为 .
2.等腰三角形的一个角为70°,它的顶角为 .
3.等腰三角形的一个角为70°,它的另外两个角为 .
4.等腰三角形的一个内角的外角为100°,它的顶角为 .
40°
40°或70°
40°,70°或55°,55°
80°或20°
练一练
5.等腰三角形的一个内角的外角为80°,它的顶角为 .
6.等腰三角形一腰上的高与底边的夹角为40°,则顶角为 .
7.等腰三角形一腰上的高与另一腰的夹角为40°,则顶角为 .
80°
50°或130°
100°
练一练
8.如图,在△ABC中,D在AC上,且BD=BC=AD,求△ABC各内角的度数?
练一练
A
B
C
D
9.如图,在△ABC中,点D、E在△ABC的边BC上,且AB=AC,AD=AE,此时BD与CE有什么关系?请说明理由.(至少两种方法证明)
一展身手
A
B
C
D
E
10.已知,如图,AB=BC=CD=ED=EF. ∠A=15°,试求∠FEM的度数?
一展身手
M
N
A
B
C
D
E
F
11.如图,钢架中A=16°,焊上等长的钢条BC,CD,DE…来加固钢架,若AB=BC,则这样的钢条至多需要多少根?
一展身手
A
B
C
D
E
再见
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
