浙教版>八年级上册2.7探索勾股定理(第1课时)(共27张PPT)
文档属性
| 名称 | 浙教版>八年级上册2.7探索勾股定理(第1课时)(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 615.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 11:49:59 | ||
图片预览



文档简介
(共27张PPT)
2.7 探索勾股定理(一)
浙教版《数学》八年级上册
教学目标
1.体验勾股定理的探索过程,掌握勾股定理;
2.会用勾股定理解决简单的几何问题.
1.创设情景,体会数学所蕴含的美;
2.通过追溯勾股定理的历史,增强学生的爱国情感.
通过合作学习和拼图验证勾股定理,培养学生合作意识,体会数形结合的思想.
知识目标
能力目标
情感目标
新课引入
假如我们一旦和外星人见面,该使用什么语言呢?
使用“符号语言”与外星人联系是最经济最有效的,外星人也最肯能使用这种语言,并且最可能是数学语言.
中国数学家华罗庚认为,我们可以用两个图形作为与外星人交谈的媒介,一个是“数”,另一个是“数形关系”(勾股定理).因为这种自然图形所具备的“数形关系”在整个宇宙中最普遍.
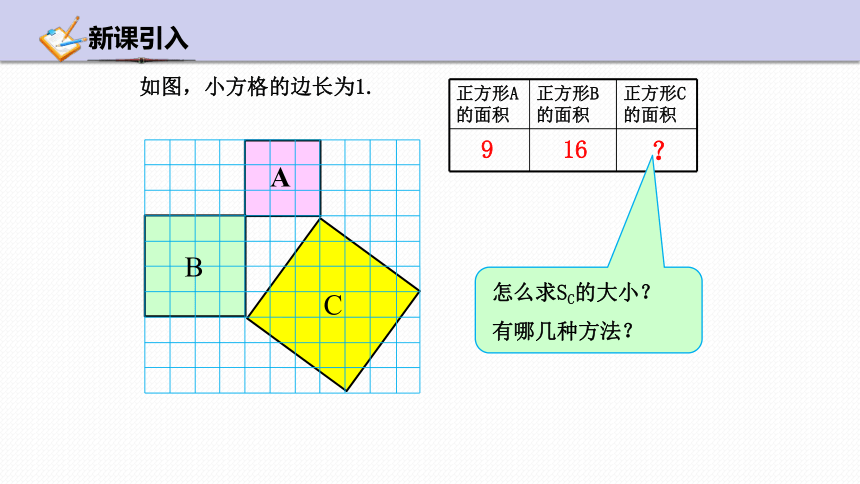
正方形A的面积 正方形B的面积 正方形C的面积
9
16
?
如图,小方格的边长为1.
A
B
C
新课引入
怎么求SC的大小?
有哪几种方法?
如图,小方格的边长为1.
A
B
C
新课引入
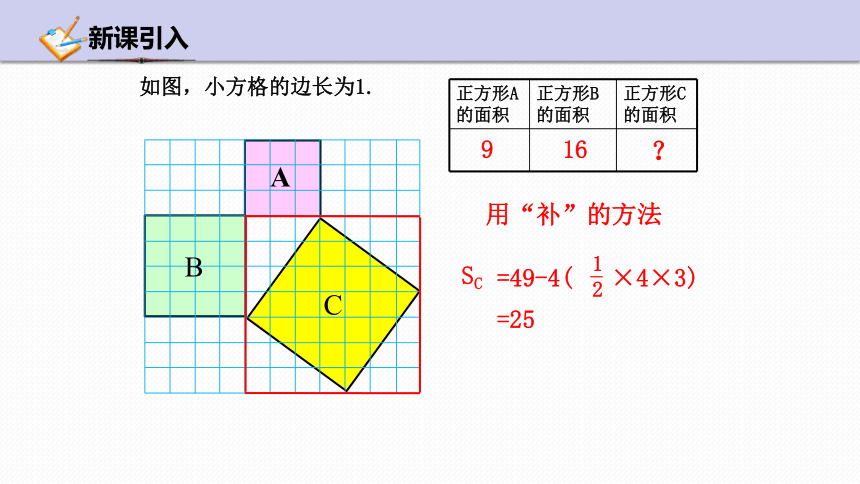
用“补”的方法
SC
正方形A的面积 正方形B的面积 正方形C的面积
9
16
?
=49-4( ×4×3)
1
2
-
=25
如图,小方格的边长为1.
A
B
C
新课引入
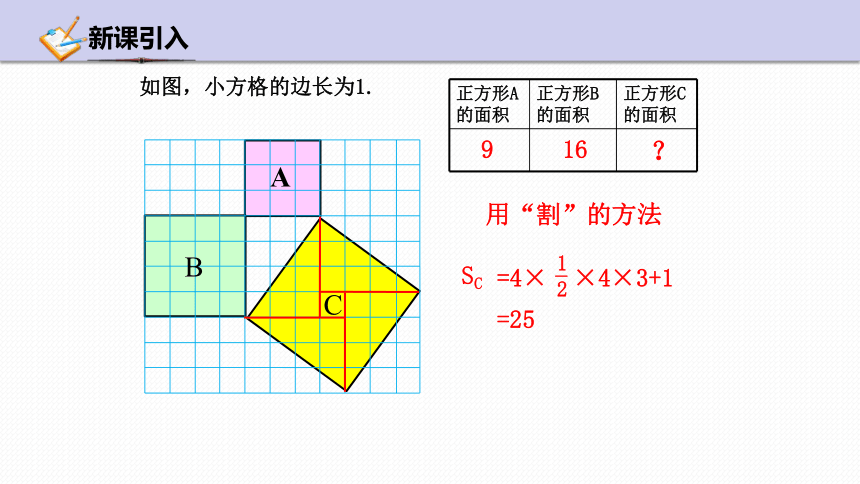
用“割”的方法
SC
正方形A的面积 正方形B的面积 正方形C的面积
9
16
?
=4× ×4×3+1
1
2
-
=25
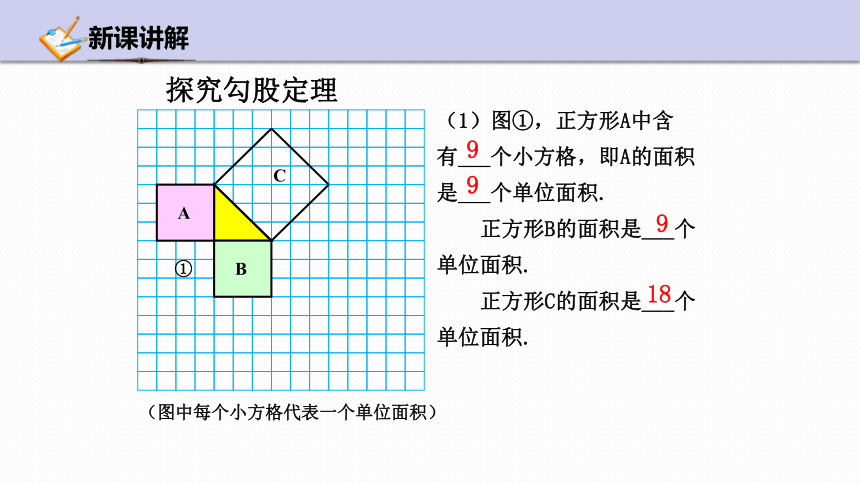
(图中每个小方格代表一个单位面积)
(1)图①,正方形A中含
有 个小方格,即A的面积
是 个单位面积.
正方形B的面积是___个
单位面积.
正方形C的面积是___个
单位面积.
9
9
9
18
探究勾股定理
新课讲解
A
B
C
①
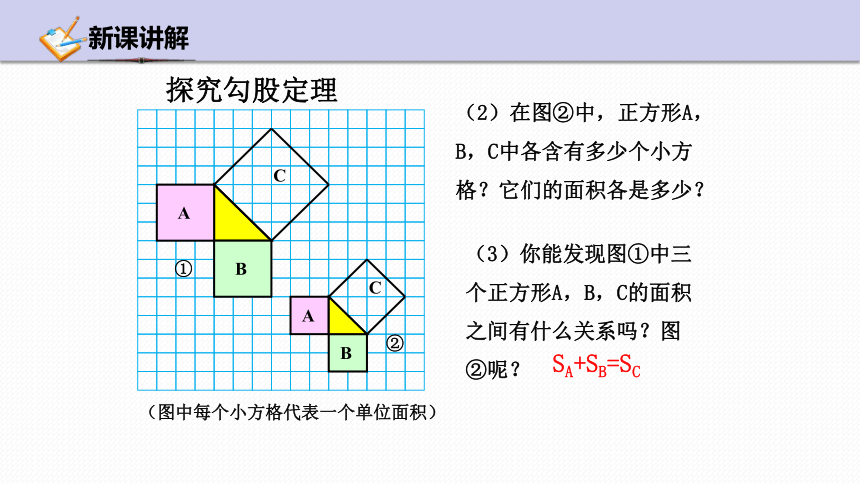
(图中每个小方格代表一个单位面积)
探究勾股定理
新课讲解
A
B
C
①
A
B
C
②
(2)在图②中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图①中三个正方形A,B,C的面积之间有什么关系吗?图②呢?
SA+SB=SC
┏
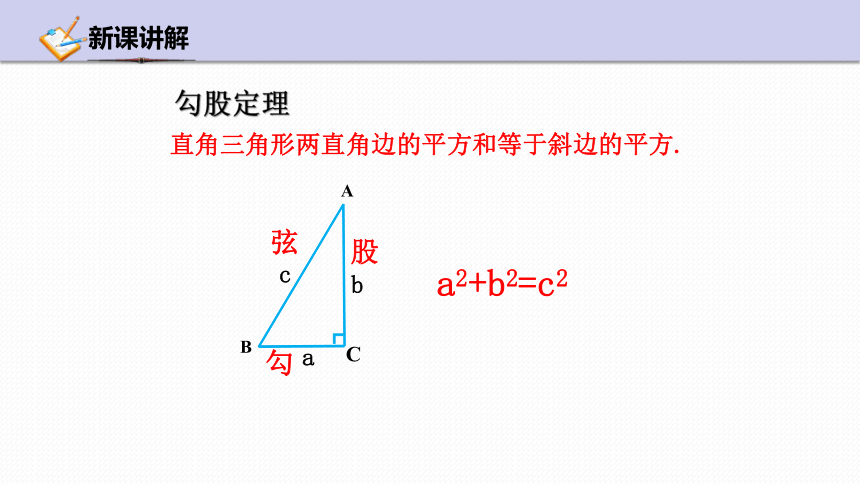
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理
B
A
C
新课讲解
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为 .
c2
验证1
c
a
b
c
a
b
c
a
b
c
a
b
4· +(b- a)2
ab
2
—
∵ c2= 4 +(b-a)2
ab
2
—
新课讲解
a2 +2ab+b2 =2ab+c2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为 .
(a+b)2
验证2
c
a
b
c
a
b
c
a
b
c
a
b
4· +c2
ab
2
—
∵ (a+b)2= 4 +c2
ab
2
—
新课讲解
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
新课讲解
数学文化
因此把这个定理命名为“勾股定理”或“商高定理”,在西方,被称为“毕达哥拉斯”定理.
图1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.
图2是在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
图1
图2
新课讲解
例题讲解
例1 已知△ABC中,∠C=Rt∠,BC=a,AC=b,AB=C.
若a=1, b=2, 求c;
若a=15, c=17, 求b;
解:
(1)根据勾股定理,得
c2=a2 +b2
=12 +22
=5
∵c>0
∴c=
例题讲解
例1 已知△ABC中,∠C=Rt∠,BC=a,AC=b,AB=C.
若a=1, b=2, 求c;
若a=15, c=17, 求b;
解:
(2)根据勾股定理,得
b2 = c2-a2
=172 -152
=64
∵b>0
∴c=8
勾股定理的主要作用 :
在直角三角形中,
① 已知任意两边求第三边的长;
② 已知一边及另两边的关系,求另两边.
新课讲解
(1)a=3, b=4,则c=____.
(2)c =17,a=8,则b=____.
(3)c=61,b=60,则a=____.
c
a
b
B
A
C
(4)a:b=3:4,c=10则a=____,b=____.
5
15
11
6
8
做一做
填空
例2 如图所示是一个长方形零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)
C
160
90
40
40
B
A
过点A作铅垂线,过点B作水平线,两线交于点C,则∠ACB=90°.
AB2 = AC2+BC2
∵AB>0
∴AB=130(mm)
解:
∵AC=90-40=50(mm)
BC=160-40=120(mm)
根据勾股定理,得
=502 +1202
=16900(mm)
答:两孔中心A, B之间的距离为130mm.
温馨提示:在实际问题中,要会根据需要构造直角三角形,再通过勾股定理来解决问题.
例题讲解
1.在△ABC中,∠C=90°.
(1)若a=5,b=12,则c= .
(2)若c=4,b= ,则a= .
2.已知△ABC的三边分别是a,b,c,若∠B=Rt∠,则有关系式( )
A.a2+b2=c2
B.a2+c2=b2
C.a2-b2=c2
D.b2+c2=a2
练一练
3. 已知△ABC中,∠C=Rt∠,BC=a,AC=b,AB=C
已知: a= ,b= , 求c;
(2)已知:c=34,a:b=8:15,求a,b.
4
5
—
3
5
—
练一练
4.下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.
=625
225
400
A
225
81
B
=144
练一练
5.如图,将长为10米的梯子AC斜靠在墙上,BC长为6米.
A
B
C
10
6
(1)求梯子上端A到墙的底端B的距离AB.
(2)若梯子下部C向后移动2米到C1点,那么梯子上部A向下移动了多少米?
A1
C1
2
练一练
A
B
C
D
7cm
6.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为_____cm2.
49
一展身手
7.以直角三角形三边为边作等边三角形,这3个等边三角形的面积之间有什么关系?
A
B
C
D
E
F
一展身手
小结
直角三角形两直角边a ,b的平方和,等于斜边为c的平方. 即
1.勾股定理:
c
a
b
B
A
C
勾
弦
股
2.公式变形:
a2 = c2 – b2
b2 = c2 – a2
c=
a=
b=
a2 + b2 = c2
在直角三角形中,
① 已知任意两边求第三边的长;
② 已知一边及另两边的关系,求另两边.
3.勾股定理的主要用途是 :
小结
再见
2.7 探索勾股定理(一)
浙教版《数学》八年级上册
教学目标
1.体验勾股定理的探索过程,掌握勾股定理;
2.会用勾股定理解决简单的几何问题.
1.创设情景,体会数学所蕴含的美;
2.通过追溯勾股定理的历史,增强学生的爱国情感.
通过合作学习和拼图验证勾股定理,培养学生合作意识,体会数形结合的思想.
知识目标
能力目标
情感目标
新课引入
假如我们一旦和外星人见面,该使用什么语言呢?
使用“符号语言”与外星人联系是最经济最有效的,外星人也最肯能使用这种语言,并且最可能是数学语言.
中国数学家华罗庚认为,我们可以用两个图形作为与外星人交谈的媒介,一个是“数”,另一个是“数形关系”(勾股定理).因为这种自然图形所具备的“数形关系”在整个宇宙中最普遍.
正方形A的面积 正方形B的面积 正方形C的面积
9
16
?
如图,小方格的边长为1.
A
B
C
新课引入
怎么求SC的大小?
有哪几种方法?
如图,小方格的边长为1.
A
B
C
新课引入
用“补”的方法
SC
正方形A的面积 正方形B的面积 正方形C的面积
9
16
?
=49-4( ×4×3)
1
2
-
=25
如图,小方格的边长为1.
A
B
C
新课引入
用“割”的方法
SC
正方形A的面积 正方形B的面积 正方形C的面积
9
16
?
=4× ×4×3+1
1
2
-
=25
(图中每个小方格代表一个单位面积)
(1)图①,正方形A中含
有 个小方格,即A的面积
是 个单位面积.
正方形B的面积是___个
单位面积.
正方形C的面积是___个
单位面积.
9
9
9
18
探究勾股定理
新课讲解
A
B
C
①
(图中每个小方格代表一个单位面积)
探究勾股定理
新课讲解
A
B
C
①
A
B
C
②
(2)在图②中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图①中三个正方形A,B,C的面积之间有什么关系吗?图②呢?
SA+SB=SC
┏
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理
B
A
C
新课讲解
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为 .
c2
验证1
c
a
b
c
a
b
c
a
b
c
a
b
4· +(b- a)2
ab
2
—
∵ c2= 4 +(b-a)2
ab
2
—
新课讲解
a2 +2ab+b2 =2ab+c2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为 .
(a+b)2
验证2
c
a
b
c
a
b
c
a
b
c
a
b
4· +c2
ab
2
—
∵ (a+b)2= 4 +c2
ab
2
—
新课讲解
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
新课讲解
数学文化
因此把这个定理命名为“勾股定理”或“商高定理”,在西方,被称为“毕达哥拉斯”定理.
图1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.
图2是在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
图1
图2
新课讲解
例题讲解
例1 已知△ABC中,∠C=Rt∠,BC=a,AC=b,AB=C.
若a=1, b=2, 求c;
若a=15, c=17, 求b;
解:
(1)根据勾股定理,得
c2=a2 +b2
=12 +22
=5
∵c>0
∴c=
例题讲解
例1 已知△ABC中,∠C=Rt∠,BC=a,AC=b,AB=C.
若a=1, b=2, 求c;
若a=15, c=17, 求b;
解:
(2)根据勾股定理,得
b2 = c2-a2
=172 -152
=64
∵b>0
∴c=8
勾股定理的主要作用 :
在直角三角形中,
① 已知任意两边求第三边的长;
② 已知一边及另两边的关系,求另两边.
新课讲解
(1)a=3, b=4,则c=____.
(2)c =17,a=8,则b=____.
(3)c=61,b=60,则a=____.
c
a
b
B
A
C
(4)a:b=3:4,c=10则a=____,b=____.
5
15
11
6
8
做一做
填空
例2 如图所示是一个长方形零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)
C
160
90
40
40
B
A
过点A作铅垂线,过点B作水平线,两线交于点C,则∠ACB=90°.
AB2 = AC2+BC2
∵AB>0
∴AB=130(mm)
解:
∵AC=90-40=50(mm)
BC=160-40=120(mm)
根据勾股定理,得
=502 +1202
=16900(mm)
答:两孔中心A, B之间的距离为130mm.
温馨提示:在实际问题中,要会根据需要构造直角三角形,再通过勾股定理来解决问题.
例题讲解
1.在△ABC中,∠C=90°.
(1)若a=5,b=12,则c= .
(2)若c=4,b= ,则a= .
2.已知△ABC的三边分别是a,b,c,若∠B=Rt∠,则有关系式( )
A.a2+b2=c2
B.a2+c2=b2
C.a2-b2=c2
D.b2+c2=a2
练一练
3. 已知△ABC中,∠C=Rt∠,BC=a,AC=b,AB=C
已知: a= ,b= , 求c;
(2)已知:c=34,a:b=8:15,求a,b.
4
5
—
3
5
—
练一练
4.下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.
=625
225
400
A
225
81
B
=144
练一练
5.如图,将长为10米的梯子AC斜靠在墙上,BC长为6米.
A
B
C
10
6
(1)求梯子上端A到墙的底端B的距离AB.
(2)若梯子下部C向后移动2米到C1点,那么梯子上部A向下移动了多少米?
A1
C1
2
练一练
A
B
C
D
7cm
6.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为_____cm2.
49
一展身手
7.以直角三角形三边为边作等边三角形,这3个等边三角形的面积之间有什么关系?
A
B
C
D
E
F
一展身手
小结
直角三角形两直角边a ,b的平方和,等于斜边为c的平方. 即
1.勾股定理:
c
a
b
B
A
C
勾
弦
股
2.公式变形:
a2 = c2 – b2
b2 = c2 – a2
c=
a=
b=
a2 + b2 = c2
在直角三角形中,
① 已知任意两边求第三边的长;
② 已知一边及另两边的关系,求另两边.
3.勾股定理的主要用途是 :
小结
再见
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
