浙教版数学八年级上册 2.7探索勾股定理 第2课时 课件 (共25张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 2.7探索勾股定理 第2课时 课件 (共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 210.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 11:51:01 | ||
图片预览




文档简介
(共25张PPT)
2.7 探索勾股定理(二)
浙教版《数学》八年级上册
教学目标
1.经历直角三角形的判定方法(勾股定理的逆定理)的探究过程;
2.掌握从边的角度来判定直角三角形的方法:如果三角形中两边打额平方和等于第三边的平方,那么这个三角形是直角三角形.
通过创设情景,了解我国古代数学家的成就,激发学生热爱祖国的思想和求知欲.
通过探索、讨论,培养学生的逻辑思维能力.
知识目标
能力目标
情感目标
知识回顾
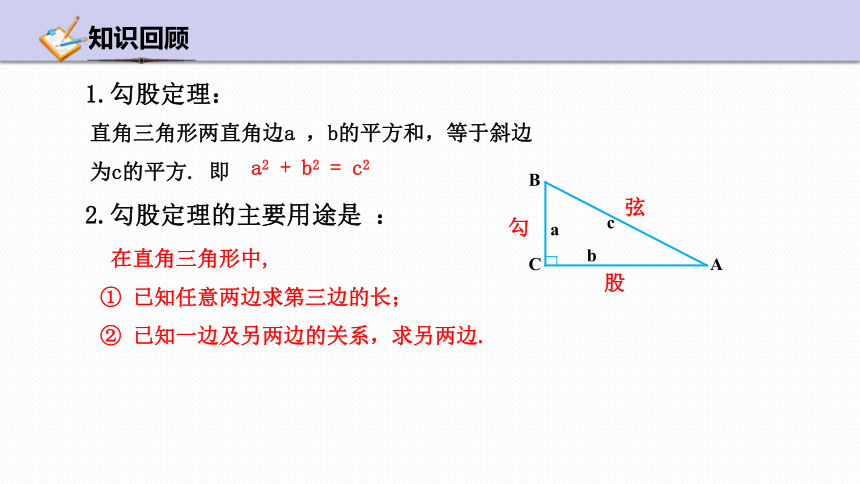
直角三角形两直角边a ,b的平方和,等于斜边为c的平方. 即
1.勾股定理:
c
a
b
B
A
C
勾
弦
股
a2 + b2 = c2
在直角三角形中,
① 已知任意两边求第三边的长;
② 已知一边及另两边的关系,求另两边.
2.勾股定理的主要用途是 :
(1)直角三角形的两直角边为3和4,则斜边为 .
(3)直角三角形的两直角边为6和8,则斜边为 .
(2)直角三角形的两直角边为5和12,则斜边为 .
(5)直角三角形的两条边为3和4,则斜边上的高是 .
(4)直角三角形的两条边为3和4,则这个直角三角形的第三边长为 .
5
5
10
13
3.填一填:
—
12
5
3√7
_
—
4
或
或
√7
_
知识回顾
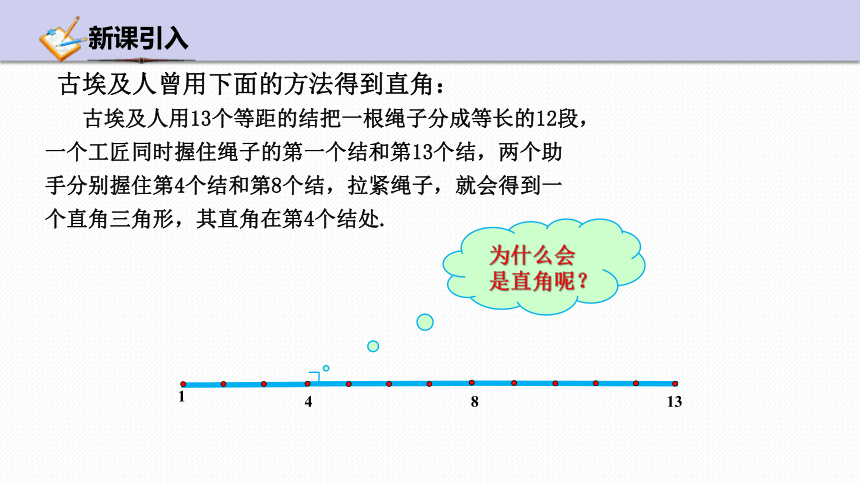
古埃及人用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第一个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.
古埃及人曾用下面的方法得到直角:
为什么会是直角呢?
1
4
8
13
新课引入
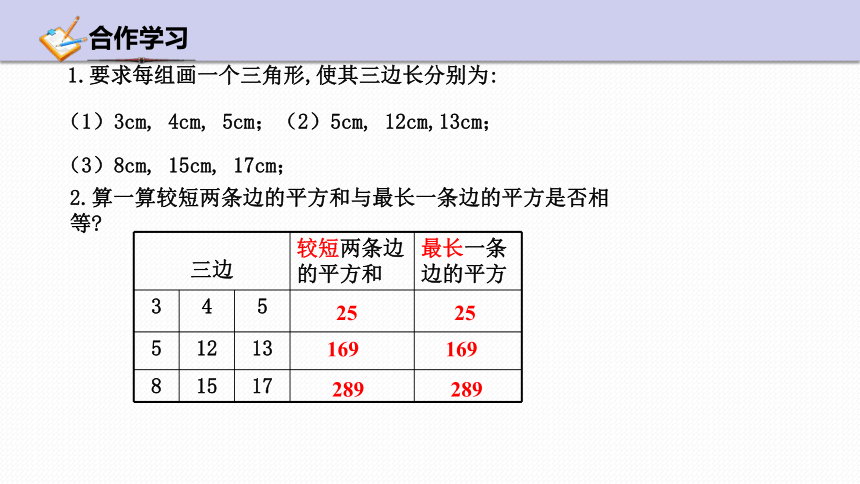
1.要求每组画一个三角形,使其三边长分别为:
(1)3cm, 4cm, 5cm;(2)5cm, 12cm,13cm;
(3)8cm, 15cm, 17cm;
2.算一算较短两条边的平方和与最长一条边的平方是否相等
三边 较短两条边的平方和 最长一条边的平方
3 4 5
5 12 13
8 15 17
25
25
169
169
289
289
合作学习
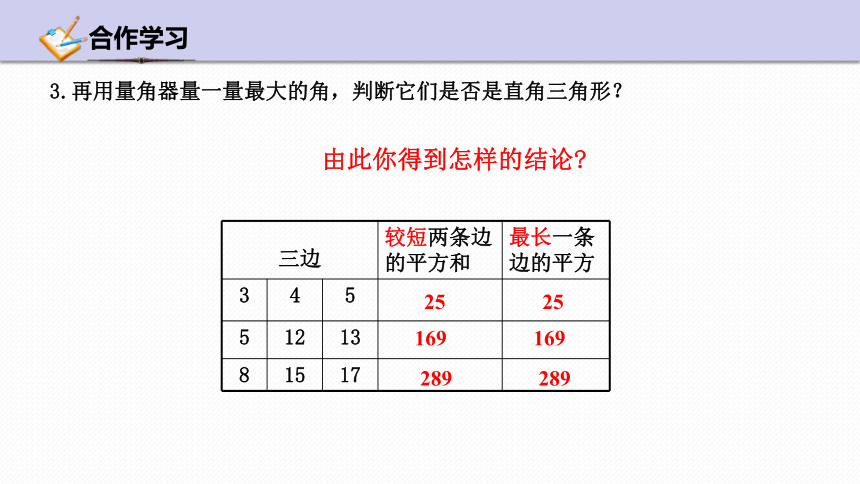
3.再用量角器量一量最大的角,判断它们是否是直角三角形?
由此你得到怎样的结论
三边 较短两条边的平方和 最长一条边的平方
3 4 5
5 12 13
8 15 17
25
25
169
169
289
289
合作学习
如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
即如果三角形的三边长a,b,c有关系
那么这个三角形是直角三角形.
勾股定理的逆定理
a2 + b2 = c2
新课讲解
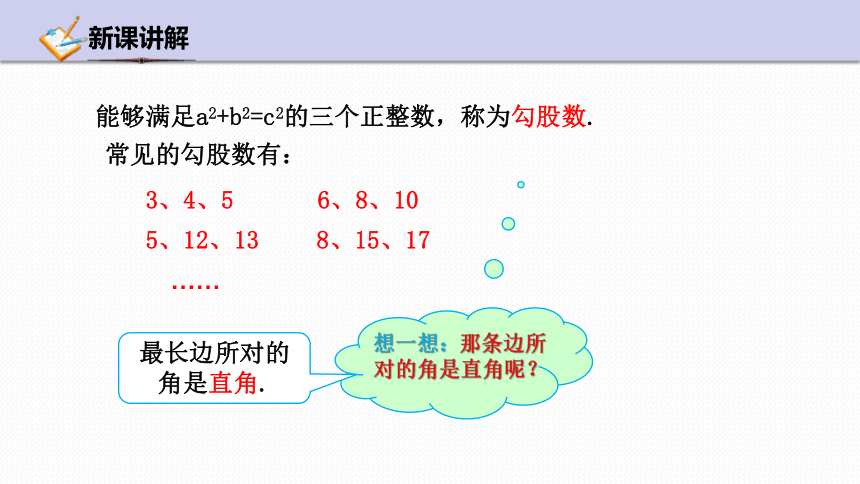
能够满足a2+b2=c2的三个正整数,称为勾股数.
常见的勾股数有:
3、4、5
6、8、10
5、12、13
8、15、17
……
想一想:那条边所对的角是直角呢?
最长边所对的角是直角.
新课讲解
2.在△ABC中BC=a,AC=b,AB=c,且b2+c2=a2, 则∠ =90°.
1.若一个三角形的三边满足a2-b2=c2 ,则这个三角形为( )
A.直角三角形 B.正三角形
C.锐角三角形 D.钝角三角形
A
A
做一做
例1 根据下列条件,分别判断以a, b, c为边的三角形是不是直角三角形
(1)a=7,b=24,c=25
(1)∵72+242=252,
∴以7, 24, 25为边三角形是直角三角形
解:
例题讲解
例1 根据下列条件,分别判断以a, b, c为边的三角形是不是直角三角形
(1)a=7,b=24,c=25
解:
(—)2+ (—)2 =
2
3
(2)∵
2
3
8
9
—
≠1
∴以 , , 1为边的三角形不是直角三角形.
2
3
—
2
3
—
例题讲解
a2+b2 c2
a2+b2 c2
a2+b2 c2
<
=
>
a
b
c
b
b
a
c
c
a
锐角三角形
直角三角形
钝角三角形
新课讲解
总结
3.根据下列条件,判断下面以a、b、c 为边的三角形是不是直角三角形
(1) a=5,b=7,c=8
(2)
(3) a=3n,b=4n,c=5n (n是正整数)
(4) a: b: c=5:12:13
做一做
例2 已知△ABC三条边长分别为a, b, c,且a=m2-n2,b=2mn,c=m2+n2(m>n,m, n是正整数).△ABC是直角三角形吗?请说明理由.
∵ a=m2-n2,b=2mn,c=m2+n2
∴a2+b2 =(m2-n2)2+(2mn)2
=m4-2m2n2+n4+4m2n2
=(m2+n2)2
=m4+2m2n2+n4
=c2
∴△ABC是直角三角形.
解:
∴c为最大边
分析:
哪边是最长边?你是怎么判断的?
作差法
例题讲解
1.下列各组数为边长,不能组成直角三角形的是( ).
A.3,4,5 B.5,12,13
C.8,15,17 D.6,8,9
D
练一练
2.下列每一组数据中的三个数值分别为三角形的三边长,能构成直角三角形的有( ).
① 3,4,5 ②
③ 5,12,13 ④
A.1个 B.2个 C.3个 D.4个
C
练一练
3.a,b,c是△ABC的三条边长,满足下列条件但不能构成直角三角形的是( ).
A. a2+b2=c2
B.∠B=∠C-∠A
C. ∠A:∠B:∠C=3:4:5
D.a:b:c=3:4:5
C
练一练
4.已知△ABC的三条边长分别为a、b、c,且满足关系:
2b(c+2b)+(2c+a)(2c-a)=3(b+c)2-4bc ,
试判断△ABC的形状,并说明理由.
练一练
变式:已知△ABC的三条边长分别为a、b、c,且满足关系:
(a+b)2 + c2 = 3ab + c(a+b),
试判断△ABC的形状,并说明理由.
练一练
5.有一块田地的形状和尺寸如图所示,∠B=∠D=90°, ∠A=60°,AB=5米,AD=4米,试求它的面积。
∟
A
B
C
D
5
∟
4
练一练
6.如图,四边形ABCD中,AB=3,BC=4,CD=12,
AD=13, ∠B=90°,求四边形ABCD的面积.
┐
D
B
A
C
一展身手
5
变式:若零件的形状及边长如图所示,你还能求面积吗
A
B
C
D
3
12
13
4
一展身手
小结
如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
1.勾股定理的逆定理
2.如果三角形的三边长分别为a,b,c
a2 + b2 = c2
锐角三角形
直角三角形
钝角三角形
a2 + b2 > c2
a2 + b2 < c2
再见
2.7 探索勾股定理(二)
浙教版《数学》八年级上册
教学目标
1.经历直角三角形的判定方法(勾股定理的逆定理)的探究过程;
2.掌握从边的角度来判定直角三角形的方法:如果三角形中两边打额平方和等于第三边的平方,那么这个三角形是直角三角形.
通过创设情景,了解我国古代数学家的成就,激发学生热爱祖国的思想和求知欲.
通过探索、讨论,培养学生的逻辑思维能力.
知识目标
能力目标
情感目标
知识回顾
直角三角形两直角边a ,b的平方和,等于斜边为c的平方. 即
1.勾股定理:
c
a
b
B
A
C
勾
弦
股
a2 + b2 = c2
在直角三角形中,
① 已知任意两边求第三边的长;
② 已知一边及另两边的关系,求另两边.
2.勾股定理的主要用途是 :
(1)直角三角形的两直角边为3和4,则斜边为 .
(3)直角三角形的两直角边为6和8,则斜边为 .
(2)直角三角形的两直角边为5和12,则斜边为 .
(5)直角三角形的两条边为3和4,则斜边上的高是 .
(4)直角三角形的两条边为3和4,则这个直角三角形的第三边长为 .
5
5
10
13
3.填一填:
—
12
5
3√7
_
—
4
或
或
√7
_
知识回顾
古埃及人用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第一个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.
古埃及人曾用下面的方法得到直角:
为什么会是直角呢?
1
4
8
13
新课引入
1.要求每组画一个三角形,使其三边长分别为:
(1)3cm, 4cm, 5cm;(2)5cm, 12cm,13cm;
(3)8cm, 15cm, 17cm;
2.算一算较短两条边的平方和与最长一条边的平方是否相等
三边 较短两条边的平方和 最长一条边的平方
3 4 5
5 12 13
8 15 17
25
25
169
169
289
289
合作学习
3.再用量角器量一量最大的角,判断它们是否是直角三角形?
由此你得到怎样的结论
三边 较短两条边的平方和 最长一条边的平方
3 4 5
5 12 13
8 15 17
25
25
169
169
289
289
合作学习
如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
即如果三角形的三边长a,b,c有关系
那么这个三角形是直角三角形.
勾股定理的逆定理
a2 + b2 = c2
新课讲解
能够满足a2+b2=c2的三个正整数,称为勾股数.
常见的勾股数有:
3、4、5
6、8、10
5、12、13
8、15、17
……
想一想:那条边所对的角是直角呢?
最长边所对的角是直角.
新课讲解
2.在△ABC中BC=a,AC=b,AB=c,且b2+c2=a2, 则∠ =90°.
1.若一个三角形的三边满足a2-b2=c2 ,则这个三角形为( )
A.直角三角形 B.正三角形
C.锐角三角形 D.钝角三角形
A
A
做一做
例1 根据下列条件,分别判断以a, b, c为边的三角形是不是直角三角形
(1)a=7,b=24,c=25
(1)∵72+242=252,
∴以7, 24, 25为边三角形是直角三角形
解:
例题讲解
例1 根据下列条件,分别判断以a, b, c为边的三角形是不是直角三角形
(1)a=7,b=24,c=25
解:
(—)2+ (—)2 =
2
3
(2)∵
2
3
8
9
—
≠1
∴以 , , 1为边的三角形不是直角三角形.
2
3
—
2
3
—
例题讲解
a2+b2 c2
a2+b2 c2
a2+b2 c2
<
=
>
a
b
c
b
b
a
c
c
a
锐角三角形
直角三角形
钝角三角形
新课讲解
总结
3.根据下列条件,判断下面以a、b、c 为边的三角形是不是直角三角形
(1) a=5,b=7,c=8
(2)
(3) a=3n,b=4n,c=5n (n是正整数)
(4) a: b: c=5:12:13
做一做
例2 已知△ABC三条边长分别为a, b, c,且a=m2-n2,b=2mn,c=m2+n2(m>n,m, n是正整数).△ABC是直角三角形吗?请说明理由.
∵ a=m2-n2,b=2mn,c=m2+n2
∴a2+b2 =(m2-n2)2+(2mn)2
=m4-2m2n2+n4+4m2n2
=(m2+n2)2
=m4+2m2n2+n4
=c2
∴△ABC是直角三角形.
解:
∴c为最大边
分析:
哪边是最长边?你是怎么判断的?
作差法
例题讲解
1.下列各组数为边长,不能组成直角三角形的是( ).
A.3,4,5 B.5,12,13
C.8,15,17 D.6,8,9
D
练一练
2.下列每一组数据中的三个数值分别为三角形的三边长,能构成直角三角形的有( ).
① 3,4,5 ②
③ 5,12,13 ④
A.1个 B.2个 C.3个 D.4个
C
练一练
3.a,b,c是△ABC的三条边长,满足下列条件但不能构成直角三角形的是( ).
A. a2+b2=c2
B.∠B=∠C-∠A
C. ∠A:∠B:∠C=3:4:5
D.a:b:c=3:4:5
C
练一练
4.已知△ABC的三条边长分别为a、b、c,且满足关系:
2b(c+2b)+(2c+a)(2c-a)=3(b+c)2-4bc ,
试判断△ABC的形状,并说明理由.
练一练
变式:已知△ABC的三条边长分别为a、b、c,且满足关系:
(a+b)2 + c2 = 3ab + c(a+b),
试判断△ABC的形状,并说明理由.
练一练
5.有一块田地的形状和尺寸如图所示,∠B=∠D=90°, ∠A=60°,AB=5米,AD=4米,试求它的面积。
∟
A
B
C
D
5
∟
4
练一练
6.如图,四边形ABCD中,AB=3,BC=4,CD=12,
AD=13, ∠B=90°,求四边形ABCD的面积.
┐
D
B
A
C
一展身手
5
变式:若零件的形状及边长如图所示,你还能求面积吗
A
B
C
D
3
12
13
4
一展身手
小结
如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
1.勾股定理的逆定理
2.如果三角形的三边长分别为a,b,c
a2 + b2 = c2
锐角三角形
直角三角形
钝角三角形
a2 + b2 > c2
a2 + b2 < c2
再见
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
