浙教版八年级上册3.3一元一次不等式(第1课时)(共24张PPT)
文档属性
| 名称 | 浙教版八年级上册3.3一元一次不等式(第1课时)(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 215.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 11:54:44 | ||
图片预览






文档简介
(共24张PPT)
3.3一元一次不等式(一)
浙教版《数学》八年级上册
教学目标
1.一元一次不等式及其解的概念;
2.会用不等式的基本性质解简单的一元一次不等式;
3.会在数轴上表示一元一次不等式的解.
感受不同数学模型下,运用基本性质在解题时的异同点,体会殊途同归的数学解题技巧.
培养学生数形结合的能力.
知识目标
能力目标
情感目标
不等式的基本性质:(用字母表示)
性质3:
性质1:若a<b,b<c,则a<c.
性质2:
(不等号方向不变)
(不等号方向不变)
(不等号方向改变)
(传递性)
知识回顾
如果a>b,那么a+c>b+c,a-c>b-c;
如果a<b,那么a+c<b+c,a-c<b-c.
如果a>b,且c>0,那么ac>bc,
如果a>b,且c<0,那么ac<bc,
a
c
—
b
c
—
>
a
c
—
b
c
—
<
新课引入
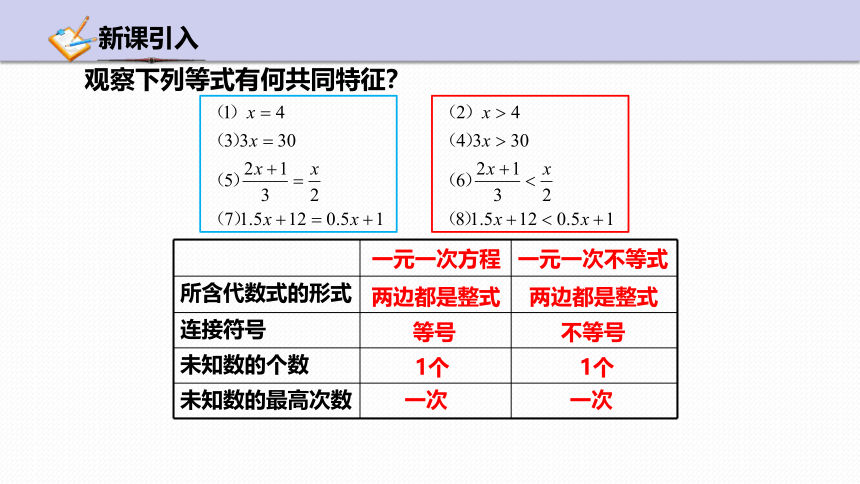
观察下列等式有何共同特征?
所含代数式的形式
连接符号
未知数的个数
未知数的最高次数
一元一次方程
两边都是整式
1个
一次
一次
1个
两边都是整式
一元一次不等式
等号
不等号
不等号的两边都是整式,而且只含有一个未知数,未知数的最高次数是一次,这样的不等式叫做一元一次不等式.
新课讲解
一元一次不等式的定义
特点:
(1)不等号的两边都是整式
(2)只含有一个未知数
(3)未知数的次数是1
1.下列不等式中,哪些是一元一次不等式
(1)4<5.1
(2)5x+3<0
不是
是
不是
不是
(5)x>5
是
做一做
(3)
(4)
我们把能使不等式成立的未知数的值的全体叫做不等式的解集,简称不等式的解.
把x=5代入不等式3x<18,不等式成立吗?
那能否说能使不等式成立的值就是x=5
新课讲解
x=6,x=7呢?
这样的值有无数个
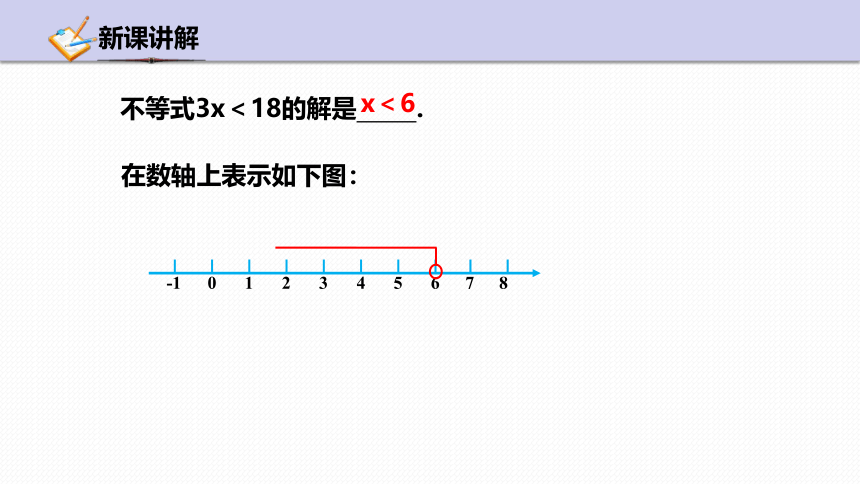
不等式3x<18的解是 .
x<6
0
1
2
3
4
5
6
-1
7
8
在数轴上表示如下图:
新课讲解
2.判断
做一做
(1) x=2是x-1>0的解 . ( )
(2) x-1﹥0的解是x=2. ( )
(3) x-1﹥0的解x>1 . ( )
(4) x-1﹥0的解是x>2 . ( )
√
√
×
×
做一做
-4, -2.5, 0, 1, 2.5,
3, 3.2, 4.8, 8, 12
3.下例数值哪些是不等式x+3>6的解?哪些不是
√
×
×
×
×
×
×
√
√
√
例题讲解
例1 解下列不等式,并把解表示在数轴上:
(1)两边都除以4,得
(1)4x<10
解:
5
2
x<
不等式的解表示在数轴上如图
5
2
0
1
2
3
4
-1
分析:
解不等式就是把不等式变形成:
“x>a”(或“x≥a”),
“x<a”(或“x≤a”)
(2)
不等式的解表示在数轴上如图
-2
-1
0
1
-3
例题讲解
例1 解下列不等式,并把解表示在数轴上:
(1)4x<10
3
5
(2)- x≥1.2
解:
x<-2
(2)两边都除以- ,得
3
5
不等式的两边同乘以(或除以)同一个负数,不等号要改变方向
4.求下列各不等式的解集
(1) x+5<3
(2) -3x>30
做一做
例题讲解
例1 解下列不等式,并把解表示在数轴上:
(1)两边都除以4,得
(1)4x<10
3
5
(2)- x≥1.2
解:
5
2
x<
不等式的解表示在数轴上如图
5
2
0
1
2
3
4
-1
-3
-2
-1
0
1
-4
例2 解不等式7x-2≤9x+3,把解表示在数轴上,并求出不等式的负整数解.
不等式的负整数解是x=-1和x=-2.
不等式的解表示在数轴上如图所示.
解:
先在不等式的两边同加上-9x,得
7x-9x-2≤3
再在不等式的两边同加上2,得
7x-9x≤3+2.
合并同类项,得
两边同除以-2,得
-2x≤5
x≥-
5
2
—
5
2
-
移项,得
把不等式中的任何一项的符号改变后,从不等号的一边移到另一边,所得到的不等式仍成立.也就是说,在解不等式时,移项法则同样适用.
例题讲解
5.根据数轴上表示的不等式的解,写出不等式的特殊解:
自然数解:________
负整数解:_____
0
2
0
-2
0
-3
最小的正整数解:____
0,1,2
-1
1
做一做
1.不等式(a+1)x>(a+1)的解集是x<1,则a的取值范围是( )
A. a<0 B. a<1
C. a<-1 D. a>-1
C
练一练
2.下列不等式的解法正确吗?
(1)-2x<-4.
解:两边同除以-2,得x<-2;
不正确.应改为x>2.
(2) x+1>2x-3.
解:移项,得 4>x,即 x>4.
不正确.应改为x<4.
练一练
3.解下列不等式,并把解表示在数轴上:
(1)1-x>2; (2)5x-4>4-3x;
(3) ≤1; (4)6x-1>9x-4.
练一练
4.解不等式0.5x-3>-14-2.5x,把解表示在数轴上,并求出适合不等式的最大负整数和最小正整数.
练一练
5.已知关于x的不等式ax<8的正整数解只有1和2两个,求整数a的取值范围.
一展身手
6.如果关于x 的不等式(a+1)<2的自然数解有且只有一个,试求a的取值范围.
一展身手
小结
一元一次不等式 一元一次方程
定义
解的个数
解题依据
移项符号是否改变
一般情况无数个
1个
若a若a>b,且c>0,那么ac>bc.
若a>b,且c<0,那么ac若a=b,则a+c=b+c.
若a=b,且c>0,那么ac=bc.
若a=b,且c<0,那么ac=bc.
改变所移项的符号
改变所移项的符号
①不等号两边都是整式
②一次只含有一个未知数
③未知数的最高次数是一次
①等号两边都是整式
②一次只含有一个未知数
③未知数的最高次数是一次
再见
3.3一元一次不等式(一)
浙教版《数学》八年级上册
教学目标
1.一元一次不等式及其解的概念;
2.会用不等式的基本性质解简单的一元一次不等式;
3.会在数轴上表示一元一次不等式的解.
感受不同数学模型下,运用基本性质在解题时的异同点,体会殊途同归的数学解题技巧.
培养学生数形结合的能力.
知识目标
能力目标
情感目标
不等式的基本性质:(用字母表示)
性质3:
性质1:若a<b,b<c,则a<c.
性质2:
(不等号方向不变)
(不等号方向不变)
(不等号方向改变)
(传递性)
知识回顾
如果a>b,那么a+c>b+c,a-c>b-c;
如果a<b,那么a+c<b+c,a-c<b-c.
如果a>b,且c>0,那么ac>bc,
如果a>b,且c<0,那么ac<bc,
a
c
—
b
c
—
>
a
c
—
b
c
—
<
新课引入
观察下列等式有何共同特征?
所含代数式的形式
连接符号
未知数的个数
未知数的最高次数
一元一次方程
两边都是整式
1个
一次
一次
1个
两边都是整式
一元一次不等式
等号
不等号
不等号的两边都是整式,而且只含有一个未知数,未知数的最高次数是一次,这样的不等式叫做一元一次不等式.
新课讲解
一元一次不等式的定义
特点:
(1)不等号的两边都是整式
(2)只含有一个未知数
(3)未知数的次数是1
1.下列不等式中,哪些是一元一次不等式
(1)4<5.1
(2)5x+3<0
不是
是
不是
不是
(5)x>5
是
做一做
(3)
(4)
我们把能使不等式成立的未知数的值的全体叫做不等式的解集,简称不等式的解.
把x=5代入不等式3x<18,不等式成立吗?
那能否说能使不等式成立的值就是x=5
新课讲解
x=6,x=7呢?
这样的值有无数个
不等式3x<18的解是 .
x<6
0
1
2
3
4
5
6
-1
7
8
在数轴上表示如下图:
新课讲解
2.判断
做一做
(1) x=2是x-1>0的解 . ( )
(2) x-1﹥0的解是x=2. ( )
(3) x-1﹥0的解x>1 . ( )
(4) x-1﹥0的解是x>2 . ( )
√
√
×
×
做一做
-4, -2.5, 0, 1, 2.5,
3, 3.2, 4.8, 8, 12
3.下例数值哪些是不等式x+3>6的解?哪些不是
√
×
×
×
×
×
×
√
√
√
例题讲解
例1 解下列不等式,并把解表示在数轴上:
(1)两边都除以4,得
(1)4x<10
解:
5
2
x<
不等式的解表示在数轴上如图
5
2
0
1
2
3
4
-1
分析:
解不等式就是把不等式变形成:
“x>a”(或“x≥a”),
“x<a”(或“x≤a”)
(2)
不等式的解表示在数轴上如图
-2
-1
0
1
-3
例题讲解
例1 解下列不等式,并把解表示在数轴上:
(1)4x<10
3
5
(2)- x≥1.2
解:
x<-2
(2)两边都除以- ,得
3
5
不等式的两边同乘以(或除以)同一个负数,不等号要改变方向
4.求下列各不等式的解集
(1) x+5<3
(2) -3x>30
做一做
例题讲解
例1 解下列不等式,并把解表示在数轴上:
(1)两边都除以4,得
(1)4x<10
3
5
(2)- x≥1.2
解:
5
2
x<
不等式的解表示在数轴上如图
5
2
0
1
2
3
4
-1
-3
-2
-1
0
1
-4
例2 解不等式7x-2≤9x+3,把解表示在数轴上,并求出不等式的负整数解.
不等式的负整数解是x=-1和x=-2.
不等式的解表示在数轴上如图所示.
解:
先在不等式的两边同加上-9x,得
7x-9x-2≤3
再在不等式的两边同加上2,得
7x-9x≤3+2.
合并同类项,得
两边同除以-2,得
-2x≤5
x≥-
5
2
—
5
2
-
移项,得
把不等式中的任何一项的符号改变后,从不等号的一边移到另一边,所得到的不等式仍成立.也就是说,在解不等式时,移项法则同样适用.
例题讲解
5.根据数轴上表示的不等式的解,写出不等式的特殊解:
自然数解:________
负整数解:_____
0
2
0
-2
0
-3
最小的正整数解:____
0,1,2
-1
1
做一做
1.不等式(a+1)x>(a+1)的解集是x<1,则a的取值范围是( )
A. a<0 B. a<1
C. a<-1 D. a>-1
C
练一练
2.下列不等式的解法正确吗?
(1)-2x<-4.
解:两边同除以-2,得x<-2;
不正确.应改为x>2.
(2) x+1>2x-3.
解:移项,得 4>x,即 x>4.
不正确.应改为x<4.
练一练
3.解下列不等式,并把解表示在数轴上:
(1)1-x>2; (2)5x-4>4-3x;
(3) ≤1; (4)6x-1>9x-4.
练一练
4.解不等式0.5x-3>-14-2.5x,把解表示在数轴上,并求出适合不等式的最大负整数和最小正整数.
练一练
5.已知关于x的不等式ax<8的正整数解只有1和2两个,求整数a的取值范围.
一展身手
6.如果关于x 的不等式(a+1)<2的自然数解有且只有一个,试求a的取值范围.
一展身手
小结
一元一次不等式 一元一次方程
定义
解的个数
解题依据
移项符号是否改变
一般情况无数个
1个
若a
若a>b,且c<0,那么ac
若a=b,且c>0,那么ac=bc.
若a=b,且c<0,那么ac=bc.
改变所移项的符号
改变所移项的符号
①不等号两边都是整式
②一次只含有一个未知数
③未知数的最高次数是一次
①等号两边都是整式
②一次只含有一个未知数
③未知数的最高次数是一次
再见
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
