浙教版数学八年级上册 3.4一元一次不等式组 课件 (共26张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 3.4一元一次不等式组 课件 (共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 250.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 11:54:21 | ||
图片预览





文档简介
(共26张PPT)
3.4一元一次不等式组
浙教版《数学》八年级上册
教学目标
1.理解一元一次不等式组的概念及不等式组的解的概念;
2.会解由两个一元一次不等式组成的不等式组,并会用数轴确定解.
感受“化难为易”、化未知为已知的数学思
想.
培养学生进行数学类比的能力.
知识目标
能力目标
情感目标
知识回顾
1.不等式-x>-2的解是( )
A.x>2 B.x>-2 C.x<2 D.x<-2
C
2.不等式( )的解在数轴表示,如图所示:
A.x>-1 B.x<-1 C.x≤-1 D.x≥-1
-2 -1 0 1 2
D
新课引入
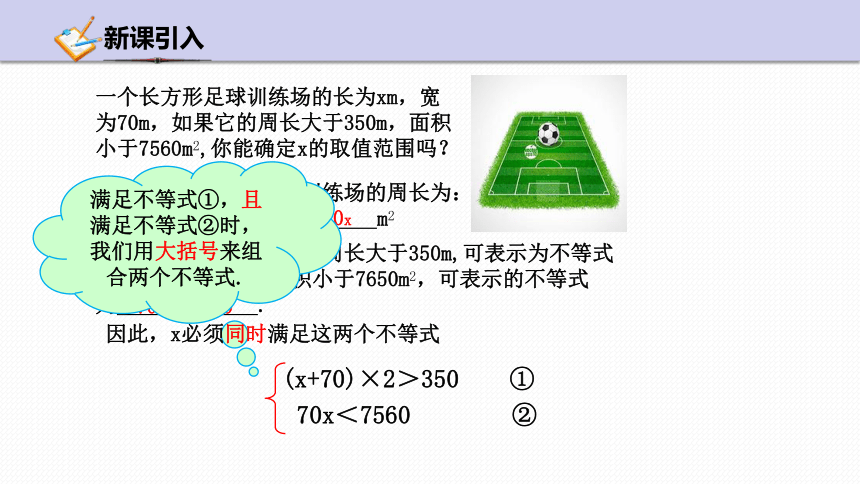
一个长方形足球训练场的长为xm,宽为70m,如果它的周长大于350m,面积小于7560m2,你能确定x的取值范围吗?
(1)这个长方形足球训练场的周长为:
m,面积为 m2
(2)根据题中长方形的周长大于350m,可表示为不等式
,面积小于7650m2,可表示的不等式为 .
(x+70)×2
(x+70)×2>350
70x
70x<7560
(x+70)×2>350 ①
70x<7560 ②
满足不等式①,且满足不等式②时,我们用大括号来组合两个不等式.
因此,x必须同时满足这两个不等式
新课讲解
(x+70)×2>350 ①
70x<7560 ②
不等式①和不等式②具有什么共同点?
观察并思考
含有同一个未知数
是一元一次不等式
定义:
一般地,有几个含同一未知数的一元
一次不等式所组成的一组不等式,叫
做一元一次不等式组.
做一做
1.下列式子中,哪些是一元一次不等式组?
是
是
不是
不是
-2 -1 0 1 2
合作学习
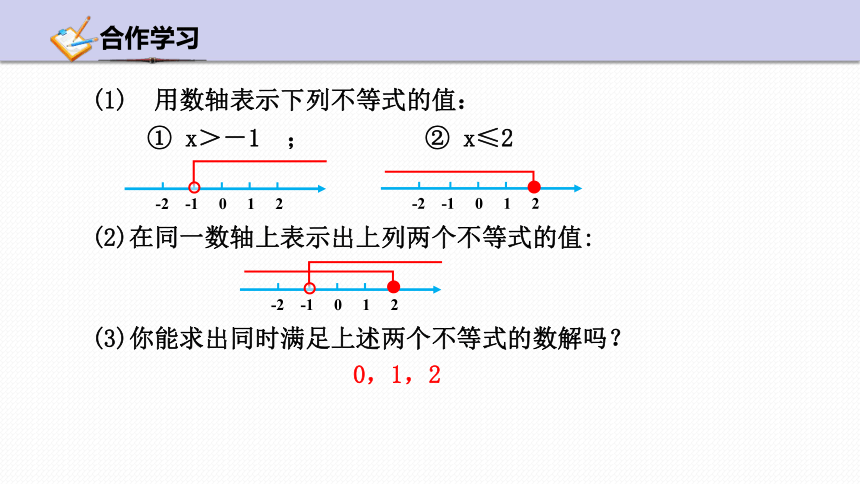
① x>-1 ; ② x≤2
(1) 用数轴表示下列不等式的值:
(2)在同一数轴上表示出上列两个不等式的值:
-2 -1 0 1 2
(3)你能求出同时满足上述两个不等式的数解吗?
0,1,2
-2 -1 0 1 2
-2 -1 0 1 2
合作学习
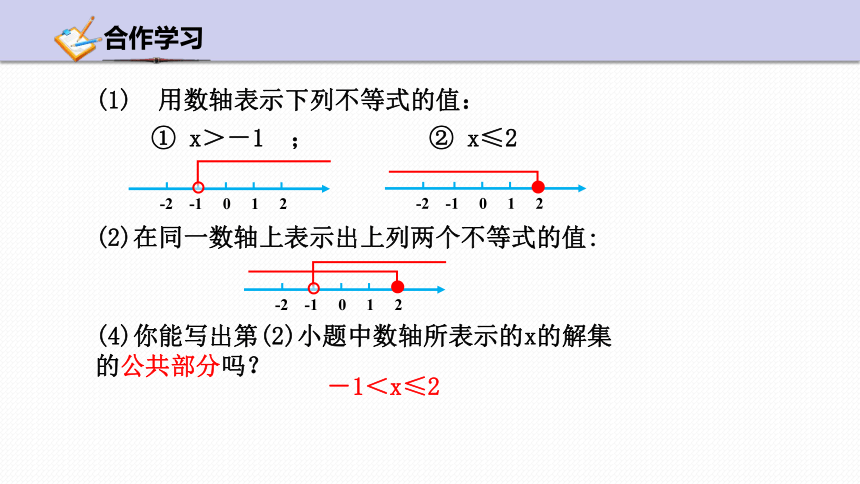
① x>-1 ; ② x≤2
(1) 用数轴表示下列不等式的值:
(2)在同一数轴上表示出上列两个不等式的值:
-2 -1 0 1 2
-2 -1 0 1 2
(4)你能写出第(2)小题中数轴所表示的x的解集的公共部分吗?
-1<x≤2
合作学习
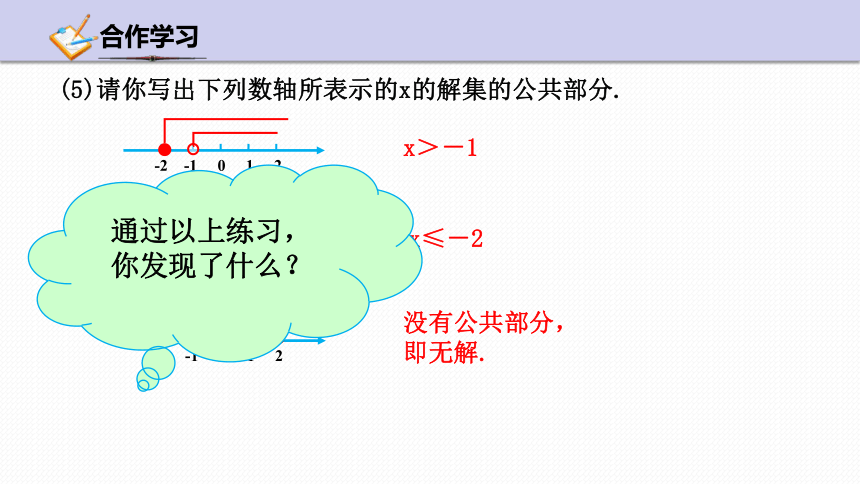
(5)请你写出下列数轴所表示的x的解集的公共部分.
x>-1
x≤-2
没有公共部分,即无解.
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
通过以上练习,
你发现了什么?
新课讲解
组成不等式组的各个不等式的解的公共部分就是不等式组的解.
定义:
注:
当它们没有公共部分时, 则称这个不等式组无解.
探究活动
利用数轴求下列不等式组的解集.
不等式组的解集是 x>2
不等式组的解集是 x<-2
-2 -1 0 1 2
-2 -1 0 1 2
同大取大
同小取小
探究活动
利用数轴求下列不等式组的解集.
不等式组的解集是 -1<x<2
无解
-2 -1 0 1 2
-2 -1 0 1 2
大小小大取中间
大大小小则无解
解集记忆方法
设a < b 在数轴上表示解 不等式组的解集 规律(口诀)
x>a
x>b
x<a
x<b
x>a
x<b
x<a
x>b
a
b
a
b
a
b
a
b
x>b
x<a
无解
a<x<b
大小小大取中间
大大小小则无解
小小取小
大大取大
探究活动
例题讲解
解:
解不等式①,得x>-1
解不等式②,得x≤6
把①, ②两不等式的解表示在数轴上(如图)
-3 -2 -1 0 1 2 3 4 5 6
所以原不等式组的解是 -1<x≤6
例1 解一元一次不等式组
x≤2 ②
3x+2>x ①
分析:
根据一元一次不等式组解的意义, 只要求出各不等式的解的公共部分即可.
新课讲解
总结
解一元一次不等式组的步骤:
(1)分别求出各不等式的解;
(2)将它们的解表示在同一数轴上;
(3)求原不等式组的解(即为它们解的公共部分).
例题讲解
所以原不等式组无解
-3 -2 -1 0 1 2 3 4 5 6
例2 解一元一次不等式组
3x-2
4
>2.5-
x
2
3-5x>x-2(2x-1)
解:
解不等式①,得x<
解不等式②,得 x>
把① ,②两个不等式的解表示在数轴上
练一练
1.解下列各一元一次不等式组:
练一练
2.若不等式组 的解为 x≥-b,
则下列各式正确的是 ( )
A.a>b B.a<b
C.b ≤a D.ab>0
A
练一练
3.已知一元一次不等式x>2和不等式组的解,求关于a的取值范围
x>2
x>a
的解是x>2,则a的取值范围是________
(1)
x>2
x>a
的解是x>a,则a的取值范围是________
(2)
x>2
x<a
的解是2<x<a,则a的取值范围是________
(4)
a≤2
a≥2
a≤2
a>2
x>2
x<a
的解是无解,则a的取值范围是________
(3)
4.解不等式组: 2-x<x≤6-2x,并求出它的整数解.
练一练
练一练
5.使方程组 的解 x、y都是正数,求a的取值范围
一展身手
6.已知关于x的不等式2(x-3)-a<1的正整数解是1,2,3,求a的取值范围.
一展身手
7. 已知关于x的不等式组
的正数解共有4个,求a的取值范围.
小结
1.一元一次不等式组的概念
2.一元一次不等式组的解的概念
有几个含同一未知数的一元一次不等式所组成的一组不等式,叫做一元一次不等式组.
组成不等式组的各个不等式的解的公共部分就是不等式组的解.
小结
3.解一元一次不等式组的步骤
(1)分别求出各不等式的解;
(2)将它们的解表示在同一数轴上;
(3)求原不等式组的解(即为它们解的公共部分).
4.一元一次不等式组解集的规律
大小小大取中间
大大小小则无解
小小取小
大大取大
再见
3.4一元一次不等式组
浙教版《数学》八年级上册
教学目标
1.理解一元一次不等式组的概念及不等式组的解的概念;
2.会解由两个一元一次不等式组成的不等式组,并会用数轴确定解.
感受“化难为易”、化未知为已知的数学思
想.
培养学生进行数学类比的能力.
知识目标
能力目标
情感目标
知识回顾
1.不等式-x>-2的解是( )
A.x>2 B.x>-2 C.x<2 D.x<-2
C
2.不等式( )的解在数轴表示,如图所示:
A.x>-1 B.x<-1 C.x≤-1 D.x≥-1
-2 -1 0 1 2
D
新课引入
一个长方形足球训练场的长为xm,宽为70m,如果它的周长大于350m,面积小于7560m2,你能确定x的取值范围吗?
(1)这个长方形足球训练场的周长为:
m,面积为 m2
(2)根据题中长方形的周长大于350m,可表示为不等式
,面积小于7650m2,可表示的不等式为 .
(x+70)×2
(x+70)×2>350
70x
70x<7560
(x+70)×2>350 ①
70x<7560 ②
满足不等式①,且满足不等式②时,我们用大括号来组合两个不等式.
因此,x必须同时满足这两个不等式
新课讲解
(x+70)×2>350 ①
70x<7560 ②
不等式①和不等式②具有什么共同点?
观察并思考
含有同一个未知数
是一元一次不等式
定义:
一般地,有几个含同一未知数的一元
一次不等式所组成的一组不等式,叫
做一元一次不等式组.
做一做
1.下列式子中,哪些是一元一次不等式组?
是
是
不是
不是
-2 -1 0 1 2
合作学习
① x>-1 ; ② x≤2
(1) 用数轴表示下列不等式的值:
(2)在同一数轴上表示出上列两个不等式的值:
-2 -1 0 1 2
(3)你能求出同时满足上述两个不等式的数解吗?
0,1,2
-2 -1 0 1 2
-2 -1 0 1 2
合作学习
① x>-1 ; ② x≤2
(1) 用数轴表示下列不等式的值:
(2)在同一数轴上表示出上列两个不等式的值:
-2 -1 0 1 2
-2 -1 0 1 2
(4)你能写出第(2)小题中数轴所表示的x的解集的公共部分吗?
-1<x≤2
合作学习
(5)请你写出下列数轴所表示的x的解集的公共部分.
x>-1
x≤-2
没有公共部分,即无解.
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
通过以上练习,
你发现了什么?
新课讲解
组成不等式组的各个不等式的解的公共部分就是不等式组的解.
定义:
注:
当它们没有公共部分时, 则称这个不等式组无解.
探究活动
利用数轴求下列不等式组的解集.
不等式组的解集是 x>2
不等式组的解集是 x<-2
-2 -1 0 1 2
-2 -1 0 1 2
同大取大
同小取小
探究活动
利用数轴求下列不等式组的解集.
不等式组的解集是 -1<x<2
无解
-2 -1 0 1 2
-2 -1 0 1 2
大小小大取中间
大大小小则无解
解集记忆方法
设a < b 在数轴上表示解 不等式组的解集 规律(口诀)
x>a
x>b
x<a
x<b
x>a
x<b
x<a
x>b
a
b
a
b
a
b
a
b
x>b
x<a
无解
a<x<b
大小小大取中间
大大小小则无解
小小取小
大大取大
探究活动
例题讲解
解:
解不等式①,得x>-1
解不等式②,得x≤6
把①, ②两不等式的解表示在数轴上(如图)
-3 -2 -1 0 1 2 3 4 5 6
所以原不等式组的解是 -1<x≤6
例1 解一元一次不等式组
x≤2 ②
3x+2>x ①
分析:
根据一元一次不等式组解的意义, 只要求出各不等式的解的公共部分即可.
新课讲解
总结
解一元一次不等式组的步骤:
(1)分别求出各不等式的解;
(2)将它们的解表示在同一数轴上;
(3)求原不等式组的解(即为它们解的公共部分).
例题讲解
所以原不等式组无解
-3 -2 -1 0 1 2 3 4 5 6
例2 解一元一次不等式组
3x-2
4
>2.5-
x
2
3-5x>x-2(2x-1)
解:
解不等式①,得x<
解不等式②,得 x>
把① ,②两个不等式的解表示在数轴上
练一练
1.解下列各一元一次不等式组:
练一练
2.若不等式组 的解为 x≥-b,
则下列各式正确的是 ( )
A.a>b B.a<b
C.b ≤a D.ab>0
A
练一练
3.已知一元一次不等式x>2和不等式组的解,求关于a的取值范围
x>2
x>a
的解是x>2,则a的取值范围是________
(1)
x>2
x>a
的解是x>a,则a的取值范围是________
(2)
x>2
x<a
的解是2<x<a,则a的取值范围是________
(4)
a≤2
a≥2
a≤2
a>2
x>2
x<a
的解是无解,则a的取值范围是________
(3)
4.解不等式组: 2-x<x≤6-2x,并求出它的整数解.
练一练
练一练
5.使方程组 的解 x、y都是正数,求a的取值范围
一展身手
6.已知关于x的不等式2(x-3)-a<1的正整数解是1,2,3,求a的取值范围.
一展身手
7. 已知关于x的不等式组
的正数解共有4个,求a的取值范围.
小结
1.一元一次不等式组的概念
2.一元一次不等式组的解的概念
有几个含同一未知数的一元一次不等式所组成的一组不等式,叫做一元一次不等式组.
组成不等式组的各个不等式的解的公共部分就是不等式组的解.
小结
3.解一元一次不等式组的步骤
(1)分别求出各不等式的解;
(2)将它们的解表示在同一数轴上;
(3)求原不等式组的解(即为它们解的公共部分).
4.一元一次不等式组解集的规律
大小小大取中间
大大小小则无解
小小取小
大大取大
再见
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
