浙教版数学八年级上册4.3坐标平面内图形的轴对称和平移 第2课时 课件(共23张PPT)
文档属性
| 名称 | 浙教版数学八年级上册4.3坐标平面内图形的轴对称和平移 第2课时 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 223.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 11:56:02 | ||
图片预览








文档简介
(共23张PPT)
4.3 坐标平面内图形的轴对称和平移(2)
浙教版《数学》八年级上册
教学目标
1.感受坐标平面内图形变换时的坐标变换;
2.了解坐标平面内图形左、右或上、下平移时的对应点之间的坐标关系;
3.会求与已知点左、右或上、下平移后的坐标.
通过对问题的共同探讨,培养学生的合作精神.
从点的运动的过程,培养学生由特例发现问题的一般规律性的能力,以及坐标意识与数形结合的数学思想.
知识目标
能力目标
情感目标
知识回顾
x
y
1
3
2
0
1
3
2
-1
-3
-2
-3
-1
-2
A
A 1
A 2
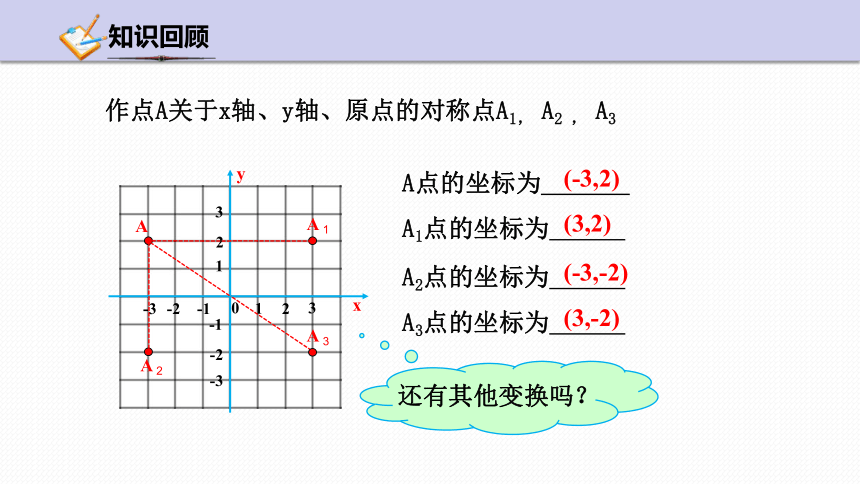
A点的坐标为 .
作点A关于x轴、y轴、原点的对称点A1, A2 , A3
A1点的坐标为 .
A2点的坐标为 .
还有其他变换吗?
(-3,2)
(3,2)
(-3,-2)
A 3
A3点的坐标为 .
(3,-2)
(__,__)
(__,__)
(__,__)
(__,__)
x
y
1
3
2
0
1
3
2
-1
-3
-2
-1
-2
4
6
5
4
合作学习
A
将点A(-3,3),B (4,5)分别作以下平移,作出相应的点,并写出点的坐标.
向上平移
3个单位
向左平移
5个单位
A(-3,3)
B(4,5)
向右平移
5个单位
A(-3,3)
B(4,5)
向下平移
3个单位
2
3
-1
5
-3
6
4
2
B
(__,__)
(__,__)
(__,__)
(__,__)
合作学习
向上平移
3个单位
向左平移
5个单位
A(-3,3)
B(4,5)
向右平移
5个单位
A(-3,3)
B(4,5)
向下平移
3个单位
2
3
-1
5
-3
6
4
2
坐标变化
横坐标 纵坐标
+5
不变
-5
不变
不变
不变
+3
-3
(1)左右平移,纵坐标不变,横坐标右 ,左 .
(2)上下平移,横坐标不变,纵坐标上 ,下 .
加
减
加
减
(1)左右平移:
右移m
(a+m, b)
左移m
(a-m, b)
(2)上下平移:
点平移的坐标变化规律
(a,b)
上移n
(a, b+n)
下移n
(a, b-n)
(a,b)
新课讲解
1.已知点A的坐标为(-2,-3),分别求点经下列平移变换后所得的像的坐标.
(1)向上平移3个单位
(3)向左平移2个单位
(-2, 0)
(-2, -6)
(-4,-3)
(2,-3)
(5)先向右平移3个单位,再向下平移3个单位
(1, -6)
(2)向下平移3个单位
(4)向右平移4个单位
做一做
做一做
2.请设计一个或一组变换,使
(1)点(2,3)变换成(-3,3)
(2)点(-3,-4)变换为(-3,0)
(3)点(-3,-4)变换为(1,0)
向左平移5个单位
向上平移4个单位
先向右平移4个单位,
再向上平移4个单位.
例题讲解
例2 如图,在直角坐标系中,平行于x轴的线段AB上所有点的纵坐标都是-1,横坐标x的取值范围是1≤x≤5 ,则线段AB上任意一点的坐标可以用“(x,-1) (1≤x ≤5)”表示,按照这样的规定,
回答下面的问题:
x
y
1
3
2
0
1
3
2
-1
4
-2
-2
4
-1
5
5
6
A
B
(1)怎样表示线段CD上任意一点的坐标?
(2, y)(-1≤y≤3)
C
D
例题讲解
例2 如图,在直角坐标系中,平行于x轴的线段AB上所有点的纵坐标都是-1,横坐标x的取值范围是1≤x≤5 ,则线段AB上任意一点的坐标可以用“(x,-1) (1≤x ≤5)”表示,按照这样的规定,
回答下面的问题:
x
y
1
3
2
0
1
3
2
-1
4
-2
-2
4
-1
5
5
6
A
B
(2)把线段AB向上平移2.5个单位,作出所得像,像上任意一点的坐标怎示?
C
D
(x, 1.5)(1≤x ≤5)
A'
B'
例题讲解
例2 如图,在直角坐标系中,平行于x轴的线段AB上所有点的纵坐标都是-1,横坐标x的取值范围是1≤x≤5 ,则线段AB上任意一点的坐标可以用“(x,-1) (1≤x ≤5)”表示,按照这样的规定,
回答下面的问题:
x
y
1
3
2
0
1
3
2
-1
4
-2
-2
4
-1
5
5
6
A
B
(3)把线段CD向左平移3个单位,作出所得像,像上任意一点的坐标怎示?
C
D
A'
B'
(-1, y)(-1≤y ≤3)
C'
D'
例题讲解
例3 如图所示
A(-8,-1)
A’(-3,4)
B(-3,-1)
B’(2,4)
x
y
0
-8
2
-4
4
-2
-6
1
6
2
4
-2
A
B
A'
B'
(1)分别求出A,A‘和点B,B’的坐标,比较A与A’,B与B’之间的坐标变化.
由A到A‘,横坐标 ,纵坐标 .
解:
由B到B‘,横坐标 ,纵坐标 .
加5
加5
加5
加5
甲
乙
例题讲解
例3 如图所示
x
y
0
-8
2
-4
4
-2
-6
1
6
2
4
-2
A
B
A'
B'
(2)图甲怎样平移到图乙.
解:
甲
乙
先向右平移5个单位
再向上平移5个单位
在图形平移中,图形中的每一个点都向相同的方向平移相同的距离.
例题讲解
x
y
0
-8
2
-4
4
-2
-6
1
6
2
4
-2
A
B
A'
B'
甲
乙
想一想:
从图甲到图乙可以看做只经历一次平移得到吗?
可以看做沿AA’的方向
平移距离为AA’的长度
的平移变换.
做一做
x
y
0
-8
2
-4
4
-2
-6
1
6
2
4
-2
A
B
甲
3.平移图甲,使点A移至O点,求点B的对应点的坐标?
A'
B'
B’(5,0)
练一练
1.点(-4,b)沿y轴正方向平移2个单位得到点(a+1,3),则a,b的值分别为( )
A.a=-3,b=3 B.a=-5,b=3
C.a=-3,b=1 D.a=-5,b=1
D
练一练
2.(1)把点P(-2,7) 向左平移2个单位,
得点 .
(2)把点P(-2,7)向下平移7个单位,得
点 .
(3)把以 (-2,7)、(-2,2)为端点的线段向右平移 7个单位,所得像上任意一点的坐标可表示为 .
(-4, 7)
(-2, 0)
(5, y)(2≤y ≤7)
练一练
3.在平面直角坐标系中,线段A1B1是由线段AB平移得到的,已知A,B两点的坐标分别为A(-2,3),B(-3,1),若点A1的坐标为(3,4),则点B1的坐标为 .
(2,2)
练一练
4.把点A(a,-3)向左平移3个单位,所得的点与点A关于y轴对称,求a的值.
5.如图,把△ABC平移,使点A变换为点O.请作出△ABC平移后的像△OB′C′,并求△OB′C′的顶点坐标和平移的距离.
一展身手
6.在直角坐标系中,把点P(a,b)先向左平移3个单位,再向上平移2个单位,再把所得的点以x轴作轴对称变换,最终所得的像为点(5,4),求点P的坐标.
一展身手
平移
右移m
(a+m, b)
左移m
(a-m, b)
点的坐标变化规律
(a,b)
上移n
(a, b+n)
下移n
(a, b-n)
新课讲解
关于x轴对称
原点对称
关于y轴对称
(a,-b)
(-a,b)
(-a,-b)
轴对称
再见
4.3 坐标平面内图形的轴对称和平移(2)
浙教版《数学》八年级上册
教学目标
1.感受坐标平面内图形变换时的坐标变换;
2.了解坐标平面内图形左、右或上、下平移时的对应点之间的坐标关系;
3.会求与已知点左、右或上、下平移后的坐标.
通过对问题的共同探讨,培养学生的合作精神.
从点的运动的过程,培养学生由特例发现问题的一般规律性的能力,以及坐标意识与数形结合的数学思想.
知识目标
能力目标
情感目标
知识回顾
x
y
1
3
2
0
1
3
2
-1
-3
-2
-3
-1
-2
A
A 1
A 2
A点的坐标为 .
作点A关于x轴、y轴、原点的对称点A1, A2 , A3
A1点的坐标为 .
A2点的坐标为 .
还有其他变换吗?
(-3,2)
(3,2)
(-3,-2)
A 3
A3点的坐标为 .
(3,-2)
(__,__)
(__,__)
(__,__)
(__,__)
x
y
1
3
2
0
1
3
2
-1
-3
-2
-1
-2
4
6
5
4
合作学习
A
将点A(-3,3),B (4,5)分别作以下平移,作出相应的点,并写出点的坐标.
向上平移
3个单位
向左平移
5个单位
A(-3,3)
B(4,5)
向右平移
5个单位
A(-3,3)
B(4,5)
向下平移
3个单位
2
3
-1
5
-3
6
4
2
B
(__,__)
(__,__)
(__,__)
(__,__)
合作学习
向上平移
3个单位
向左平移
5个单位
A(-3,3)
B(4,5)
向右平移
5个单位
A(-3,3)
B(4,5)
向下平移
3个单位
2
3
-1
5
-3
6
4
2
坐标变化
横坐标 纵坐标
+5
不变
-5
不变
不变
不变
+3
-3
(1)左右平移,纵坐标不变,横坐标右 ,左 .
(2)上下平移,横坐标不变,纵坐标上 ,下 .
加
减
加
减
(1)左右平移:
右移m
(a+m, b)
左移m
(a-m, b)
(2)上下平移:
点平移的坐标变化规律
(a,b)
上移n
(a, b+n)
下移n
(a, b-n)
(a,b)
新课讲解
1.已知点A的坐标为(-2,-3),分别求点经下列平移变换后所得的像的坐标.
(1)向上平移3个单位
(3)向左平移2个单位
(-2, 0)
(-2, -6)
(-4,-3)
(2,-3)
(5)先向右平移3个单位,再向下平移3个单位
(1, -6)
(2)向下平移3个单位
(4)向右平移4个单位
做一做
做一做
2.请设计一个或一组变换,使
(1)点(2,3)变换成(-3,3)
(2)点(-3,-4)变换为(-3,0)
(3)点(-3,-4)变换为(1,0)
向左平移5个单位
向上平移4个单位
先向右平移4个单位,
再向上平移4个单位.
例题讲解
例2 如图,在直角坐标系中,平行于x轴的线段AB上所有点的纵坐标都是-1,横坐标x的取值范围是1≤x≤5 ,则线段AB上任意一点的坐标可以用“(x,-1) (1≤x ≤5)”表示,按照这样的规定,
回答下面的问题:
x
y
1
3
2
0
1
3
2
-1
4
-2
-2
4
-1
5
5
6
A
B
(1)怎样表示线段CD上任意一点的坐标?
(2, y)(-1≤y≤3)
C
D
例题讲解
例2 如图,在直角坐标系中,平行于x轴的线段AB上所有点的纵坐标都是-1,横坐标x的取值范围是1≤x≤5 ,则线段AB上任意一点的坐标可以用“(x,-1) (1≤x ≤5)”表示,按照这样的规定,
回答下面的问题:
x
y
1
3
2
0
1
3
2
-1
4
-2
-2
4
-1
5
5
6
A
B
(2)把线段AB向上平移2.5个单位,作出所得像,像上任意一点的坐标怎示?
C
D
(x, 1.5)(1≤x ≤5)
A'
B'
例题讲解
例2 如图,在直角坐标系中,平行于x轴的线段AB上所有点的纵坐标都是-1,横坐标x的取值范围是1≤x≤5 ,则线段AB上任意一点的坐标可以用“(x,-1) (1≤x ≤5)”表示,按照这样的规定,
回答下面的问题:
x
y
1
3
2
0
1
3
2
-1
4
-2
-2
4
-1
5
5
6
A
B
(3)把线段CD向左平移3个单位,作出所得像,像上任意一点的坐标怎示?
C
D
A'
B'
(-1, y)(-1≤y ≤3)
C'
D'
例题讲解
例3 如图所示
A(-8,-1)
A’(-3,4)
B(-3,-1)
B’(2,4)
x
y
0
-8
2
-4
4
-2
-6
1
6
2
4
-2
A
B
A'
B'
(1)分别求出A,A‘和点B,B’的坐标,比较A与A’,B与B’之间的坐标变化.
由A到A‘,横坐标 ,纵坐标 .
解:
由B到B‘,横坐标 ,纵坐标 .
加5
加5
加5
加5
甲
乙
例题讲解
例3 如图所示
x
y
0
-8
2
-4
4
-2
-6
1
6
2
4
-2
A
B
A'
B'
(2)图甲怎样平移到图乙.
解:
甲
乙
先向右平移5个单位
再向上平移5个单位
在图形平移中,图形中的每一个点都向相同的方向平移相同的距离.
例题讲解
x
y
0
-8
2
-4
4
-2
-6
1
6
2
4
-2
A
B
A'
B'
甲
乙
想一想:
从图甲到图乙可以看做只经历一次平移得到吗?
可以看做沿AA’的方向
平移距离为AA’的长度
的平移变换.
做一做
x
y
0
-8
2
-4
4
-2
-6
1
6
2
4
-2
A
B
甲
3.平移图甲,使点A移至O点,求点B的对应点的坐标?
A'
B'
B’(5,0)
练一练
1.点(-4,b)沿y轴正方向平移2个单位得到点(a+1,3),则a,b的值分别为( )
A.a=-3,b=3 B.a=-5,b=3
C.a=-3,b=1 D.a=-5,b=1
D
练一练
2.(1)把点P(-2,7) 向左平移2个单位,
得点 .
(2)把点P(-2,7)向下平移7个单位,得
点 .
(3)把以 (-2,7)、(-2,2)为端点的线段向右平移 7个单位,所得像上任意一点的坐标可表示为 .
(-4, 7)
(-2, 0)
(5, y)(2≤y ≤7)
练一练
3.在平面直角坐标系中,线段A1B1是由线段AB平移得到的,已知A,B两点的坐标分别为A(-2,3),B(-3,1),若点A1的坐标为(3,4),则点B1的坐标为 .
(2,2)
练一练
4.把点A(a,-3)向左平移3个单位,所得的点与点A关于y轴对称,求a的值.
5.如图,把△ABC平移,使点A变换为点O.请作出△ABC平移后的像△OB′C′,并求△OB′C′的顶点坐标和平移的距离.
一展身手
6.在直角坐标系中,把点P(a,b)先向左平移3个单位,再向上平移2个单位,再把所得的点以x轴作轴对称变换,最终所得的像为点(5,4),求点P的坐标.
一展身手
平移
右移m
(a+m, b)
左移m
(a-m, b)
点的坐标变化规律
(a,b)
上移n
(a, b+n)
下移n
(a, b-n)
新课讲解
关于x轴对称
原点对称
关于y轴对称
(a,-b)
(-a,b)
(-a,-b)
轴对称
再见
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
