浙教版数学八年级上册5.2函数 第2课时 课件(共22张PPT)
文档属性
| 名称 | 浙教版数学八年级上册5.2函数 第2课时 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 287.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
5.2 函数 (2)
浙教版《数学》八年级上册
教学目标
1.会列简单实际问题中的函数解析式;
2.会根据函数解析式,已知自变量的值,求相应的函数值;或已知函数值,求相应自变量的值;
3.会在简单情况下求一些函数自变量的取值范围.
通过学习,进一步体验函数与生活的紧密联系,培养一种数学建模的思想.
会求一些简单的函数解析式及函数解析式的应用.
知识目标
能力目标
情感目标
知识回顾
2.函数有哪几种表示方法
解析法
列表法
图象法
1.函数的定义
一般地,在某个变化过程中,有两个变量x和y,如果对于x的每一个确定的值, y都有唯一确定的值,那么我们称y是x的函数,其中x是自变量.
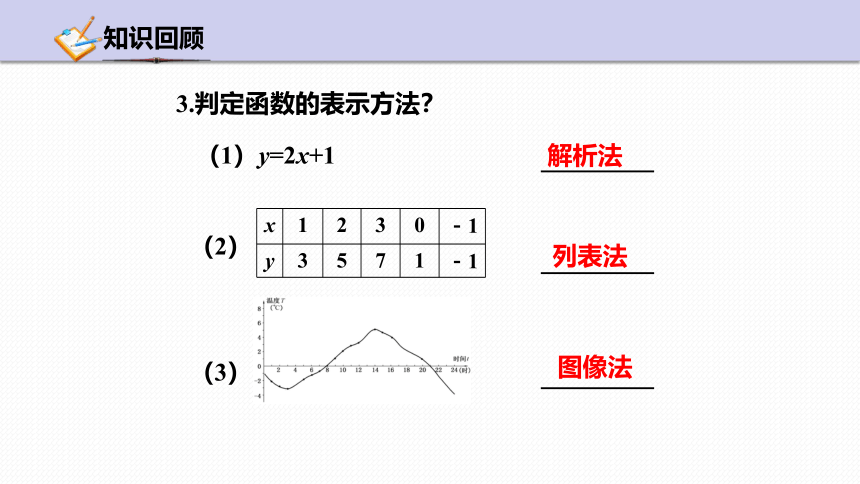
3.判定函数的表示方法?
(1)y=2x+1
解析法
列表法
图像法
知识回顾
x 1 2 3 0 -1
y 3 5 7 1 -1
(2)
(3)
问题1 求下列函数自变量的取值范围.
(2)∵2x- 4≥0
∴x≥2
(1)∵x-1≠0
∴x≠1
①代数式本身要有意义;
新课引入
解:
有分母,分母不能为零.
开2次方,被开方数是非负数.
求自变量的取值范围时,要注意什么
问题2 儿童节的时候,每人发2颗糖果,总人数x与总发的糖果数y的函数关系式为_________,
其中人数x的取值范围是_____________.
新课引入
求自变量的取值范围时,还要注意什么
y= 2x
x为正整数
②符合实际意义.
1.求下列函数中自变量x的取值范围:
做一做
例1 等腰三角形ABC的周长为10,底边BC长为y,腰AB长为x,求:
(1)由三角形的周长为10,得
解:
2x+y=10
∴ y=10-2x
例题讲解
(1)y关于x的函数解析式;
例1 等腰三角形ABC的周长为10,底边BC长为y,腰AB长为x,求:
(2)自变量x的取值范围;
(2)∵x,y是三角形的边长,
∴x>0,y>0, 2x>y
10-2x>0
2x>10-2x
例题讲解
解:
∴
解得 2.5<x<5
例1 等腰三角形ABC的周长为10,底边BC长为y,腰AB长为x,求:
(3)腰长AB=3时,底边的长
(3)当AB=3,即x=3时,
y=10-2×3=4
例题讲解
解:
∴当腰长AB=3时,底边BC=4
例1 等腰三角形ABC的周长为10,底边BC长为y,腰AB长为x,求:
例题讲解
想一想
当x=6时,y=10-2x的值是多少 对本例有意义吗
当x=2呢
当x=6时,
y=10-2×6=-2<0
解:
底边BC不存在
当x=2时,
y=10-2×2=6
边长分别为2、2、6
这样的三角形不存在.
新课讲解
函数的三类基本问题:
①求解析式
②求自变量的取值范围
③已知自变量的值求相应的函数值
或者已知函数值求相应的自变量的值
例2 游泳池应定期换水. 某游泳池在一次换水前存水936立方米,换水时打开排水孔, 以每时312立方米的速度将水放出.设放水时间为t时,游泳池内的存水量为Q立方米.
例题讲解
(1)求Q关于 t 的函数解析式和自变量 t 的取值范围;
(2)放水 2 时20分后,游泳池内还剩水多少立方米?
(3)放完游泳池内全部水需要多少时间?
2.设等腰三角形顶角度数为y,底角度数为x,则( )
A. y=180-2x(x可为全体实数)
B. y=180-2x(0≤x≤90)
C. y=180-2x (0<x<90)
D. y=180- (0<x<90)
C
练一练
3.如果一个圆筒形水管的外径是R,内径是6,它的横截面积S关于外径R的函数关系式为S=π(R2-36),那么R的取值范围为( )
A.全体实数
B.全体正实数
C.全体非负实数
D.所有大于6的实数
D
练一练
4.如图,在靠墙(墙长为18m)的地方围建一个长方形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为36m,则鸡场的面积y(m2)与宽x(m)的函数关系式为_______________,自变量的x取值范围为____________.
y=-2x2+36x
9<x<18
练一练
5.如图,正方形EFGH内接于边长为1
的正方形ABCD. 设AE= x ,
(1)试求正方形EFGH的面积y与x的
函数式,写出自变量x的取值范围.
(2) 并求当AE= 时,正方形EFGH的面积.
(3) 当x为何值时,正方形EFGH的面积是正方形ABCD 的一半.
H
G
F
E
D
C
B
A
拓展提高
6.等腰直角△ABC的直角边长与正方形MNPQ的边长均为10 cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.试写出△ABC运动过程中,重叠部分面积y cm2与MA长度x cm之间的函数关系式,并写出自变量x的范围.
拓展提高
7.某城市居民用水实行阶梯收费,每户每月用水量如果未超过20吨,按每吨1.9元收费;每户每月用水量如果超过20吨,未超过的部分仍按每吨1.9元收费,超过的部分则按每吨2.8元收费.设某户每月用水量为x吨,应交水费为y元.
(1)分别写出每月用水量未超过20吨和超过20吨时,y与x间的函数关系式;
(2)若该城市某户5月份水费平均为每吨2.2元,求该户5月份用水多少吨?
拓展提高
随 堂 作 业
小结
1.求函数自变量的取值范围时,要从两方面考虑:
①代数式要有意义
②符合实际
2.函数的三类基本问题:
①求解析式
②求自变量的取值范围
③已知自变量的值求相应的函数值
或者已知函数值求相应的自变量的值
再见
5.2 函数 (2)
浙教版《数学》八年级上册
教学目标
1.会列简单实际问题中的函数解析式;
2.会根据函数解析式,已知自变量的值,求相应的函数值;或已知函数值,求相应自变量的值;
3.会在简单情况下求一些函数自变量的取值范围.
通过学习,进一步体验函数与生活的紧密联系,培养一种数学建模的思想.
会求一些简单的函数解析式及函数解析式的应用.
知识目标
能力目标
情感目标
知识回顾
2.函数有哪几种表示方法
解析法
列表法
图象法
1.函数的定义
一般地,在某个变化过程中,有两个变量x和y,如果对于x的每一个确定的值, y都有唯一确定的值,那么我们称y是x的函数,其中x是自变量.
3.判定函数的表示方法?
(1)y=2x+1
解析法
列表法
图像法
知识回顾
x 1 2 3 0 -1
y 3 5 7 1 -1
(2)
(3)
问题1 求下列函数自变量的取值范围.
(2)∵2x- 4≥0
∴x≥2
(1)∵x-1≠0
∴x≠1
①代数式本身要有意义;
新课引入
解:
有分母,分母不能为零.
开2次方,被开方数是非负数.
求自变量的取值范围时,要注意什么
问题2 儿童节的时候,每人发2颗糖果,总人数x与总发的糖果数y的函数关系式为_________,
其中人数x的取值范围是_____________.
新课引入
求自变量的取值范围时,还要注意什么
y= 2x
x为正整数
②符合实际意义.
1.求下列函数中自变量x的取值范围:
做一做
例1 等腰三角形ABC的周长为10,底边BC长为y,腰AB长为x,求:
(1)由三角形的周长为10,得
解:
2x+y=10
∴ y=10-2x
例题讲解
(1)y关于x的函数解析式;
例1 等腰三角形ABC的周长为10,底边BC长为y,腰AB长为x,求:
(2)自变量x的取值范围;
(2)∵x,y是三角形的边长,
∴x>0,y>0, 2x>y
10-2x>0
2x>10-2x
例题讲解
解:
∴
解得 2.5<x<5
例1 等腰三角形ABC的周长为10,底边BC长为y,腰AB长为x,求:
(3)腰长AB=3时,底边的长
(3)当AB=3,即x=3时,
y=10-2×3=4
例题讲解
解:
∴当腰长AB=3时,底边BC=4
例1 等腰三角形ABC的周长为10,底边BC长为y,腰AB长为x,求:
例题讲解
想一想
当x=6时,y=10-2x的值是多少 对本例有意义吗
当x=2呢
当x=6时,
y=10-2×6=-2<0
解:
底边BC不存在
当x=2时,
y=10-2×2=6
边长分别为2、2、6
这样的三角形不存在.
新课讲解
函数的三类基本问题:
①求解析式
②求自变量的取值范围
③已知自变量的值求相应的函数值
或者已知函数值求相应的自变量的值
例2 游泳池应定期换水. 某游泳池在一次换水前存水936立方米,换水时打开排水孔, 以每时312立方米的速度将水放出.设放水时间为t时,游泳池内的存水量为Q立方米.
例题讲解
(1)求Q关于 t 的函数解析式和自变量 t 的取值范围;
(2)放水 2 时20分后,游泳池内还剩水多少立方米?
(3)放完游泳池内全部水需要多少时间?
2.设等腰三角形顶角度数为y,底角度数为x,则( )
A. y=180-2x(x可为全体实数)
B. y=180-2x(0≤x≤90)
C. y=180-2x (0<x<90)
D. y=180- (0<x<90)
C
练一练
3.如果一个圆筒形水管的外径是R,内径是6,它的横截面积S关于外径R的函数关系式为S=π(R2-36),那么R的取值范围为( )
A.全体实数
B.全体正实数
C.全体非负实数
D.所有大于6的实数
D
练一练
4.如图,在靠墙(墙长为18m)的地方围建一个长方形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为36m,则鸡场的面积y(m2)与宽x(m)的函数关系式为_______________,自变量的x取值范围为____________.
y=-2x2+36x
9<x<18
练一练
5.如图,正方形EFGH内接于边长为1
的正方形ABCD. 设AE= x ,
(1)试求正方形EFGH的面积y与x的
函数式,写出自变量x的取值范围.
(2) 并求当AE= 时,正方形EFGH的面积.
(3) 当x为何值时,正方形EFGH的面积是正方形ABCD 的一半.
H
G
F
E
D
C
B
A
拓展提高
6.等腰直角△ABC的直角边长与正方形MNPQ的边长均为10 cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.试写出△ABC运动过程中,重叠部分面积y cm2与MA长度x cm之间的函数关系式,并写出自变量x的范围.
拓展提高
7.某城市居民用水实行阶梯收费,每户每月用水量如果未超过20吨,按每吨1.9元收费;每户每月用水量如果超过20吨,未超过的部分仍按每吨1.9元收费,超过的部分则按每吨2.8元收费.设某户每月用水量为x吨,应交水费为y元.
(1)分别写出每月用水量未超过20吨和超过20吨时,y与x间的函数关系式;
(2)若该城市某户5月份水费平均为每吨2.2元,求该户5月份用水多少吨?
拓展提高
随 堂 作 业
小结
1.求函数自变量的取值范围时,要从两方面考虑:
①代数式要有意义
②符合实际
2.函数的三类基本问题:
①求解析式
②求自变量的取值范围
③已知自变量的值求相应的函数值
或者已知函数值求相应的自变量的值
再见
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
