浙教版数学八年级上册 5.3一次函数 第2课时 课件(共23张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 5.3一次函数 第2课时 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 182.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
5.3 一次函数(2)
浙教版《数学》八年级上册
教学目标
1.通过实例进一步加深对一次函数的认识;
2.会用待定系数法求一次函数的解析式,掌握待定系数法的一般步骤;
3.会通过已知自变量的值求相应的一次函数的值,会运用已知一次函数的值求相应自变量的值解决一些简单的实际问题.
通过对求一次函数解析式的方法的学习,培养学生分析问题、解决问题的能力.
能用待定系数法求一次函数的解析式.
知识目标
能力目标
情感目标
知识回顾
1.一次函数与正比例函数:
函数y=kx+b(k,b都是常数,且k≠0)叫做一次函数,
当b=0时,y=kx为正比例函数.
正比例函数是一次函数的特殊形式,
一次函数包括正比例函数.
2.一次函数与正比例函数的关系:
新课引入
(2)若x=1,y=5,则函数关系式_________.
1.已知正比例函数y=kx(k≠0)
y=5x
2.若y与x成正比例,且当x=0.5时,y=3,则y与x的关系式为_________.
y=6x
y=-x
1
3
(1)若比例系数为- , 则函数关系式为_________;
1
3
确定正比例函数的表达式需要一个条件.
新课引入
3.已知一次函数y=kx+1,在x=2时,y=-3,则k=______.
4.若一次函数y=kx+b,当x=-1时,y=2;当x=3时,y=-2.则k=______,b=______.
-1
1
确定一次例函数的表达式需要两个条件.
-2
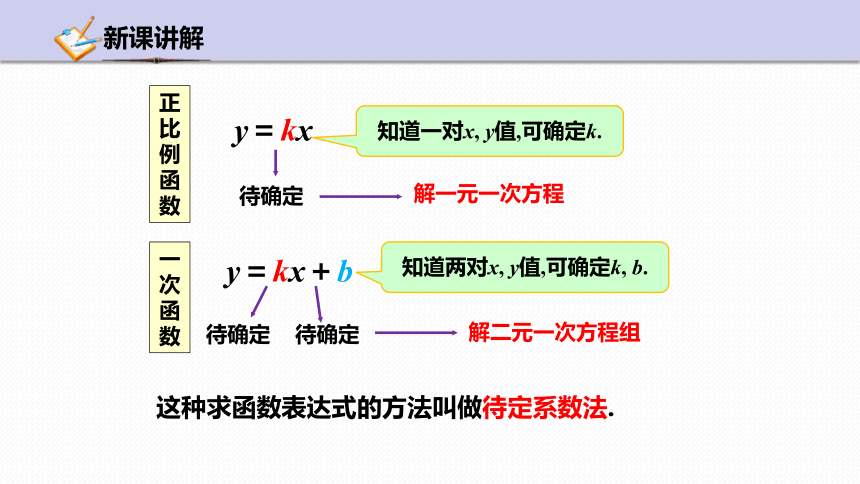
新课讲解
y=kx
y=kx+b
待确定
待确定
待确定
解一元一次方程
解二元一次方程组
正比例函数
一次函数
知道一对x, y值,可确定k.
知道两对x, y值,可确定k, b.
这种求函数表达式的方法叫做待定系数法.
新课讲解
用待定系数法求一次函数解析式的一般步骤:
1.设:
所求的一次函数解析式为y=kx+b;
2.列:
依已知列出关于k、b的方程组;
3.解:
解方程组,求得k、b;
4.答:
把k、b的值代入y=kx+b ,就得到所求的一次函数解析式.
例3 已知y是x的一次函数,当x=3时,y=1;
当x=-2时,y=-14 .求这个一次函数的关系式.
因为y是x的一次函数,所以可设所求表达
式为y=kx+b,
3k+b=1
-2k+b=-14
解得:k=3,b=-8
解:
将x=3,y=1和x=-2,y=-14分别代入上式,得
所以所求的一次函数表达式为y=3x-8.
例题讲解
做一做
1.已知y是x的一次函数,当x=-4时,y=9; x=6时,y=-1,
(1)求这个一次函数的关系式,自变量x的取值范围;
(2)当x= 时,求函数y的值;
(3)当y=7时,求自变量x的值;
(4)当y<1时,自变量x的取值范围.
做一做
2.已知y-100与x成正比例关系,且当x=10时,y=600.求y关于x的函数解析式
做一做
3.已知y+1与2x-3成正比例
(1)y是x的一次函数吗?
(2)当y=-15时,x=-1 ;当x=7时,y=1,求y关于x的一次函数解析式.
例题讲解
例4 从1995年底开始,某地区的沙漠面积几乎每年以相同的速度增长.据有关报道,到2001年底,该地区的沙漠面积已从1998年底的100.6万公顷扩展到101.2万公顷.
(1)可选用什么数学方法来描述该地区的沙漠面积的变化?
解:
(1)设95年年底沙漠面积为b万公顷,沙漠面积每年
增加k万公顷,经过x年沙漠面积为y万公顷,由题意得
y=kx+b
把x=3时,y=100.6;x=6时,y=101.2分别代入y=kx+b,得
100.6=3k+b
101.2=6k+b
解得
k=0.2
b=100
∴该地区的沙漠面积的变化由一次函数y=0.2x+100来进行描述
例题讲解
例4 从1995年底开始,某地区的沙漠面积几乎每年以相同的速度增长.据有关报道,到2001年底,该地区的沙漠面积已从1998年底的100.6万公顷扩展到101.2万公顷.
(2)如果该地区的沙漠化得不到治理,那么到2020年底,该地区的沙漠面积将增加到多少公顷?
解:
把x=25代入y=0.2x+100,得
y=0.2×25+100
=5+100
=105(万公顷)
如果该地区的沙漠化得不到治理,那么到2020年底,该地区的沙漠面积将增加到105万公顷
练一练
4.已知y是x一次函数,当x=-2时, y=7;当x=3时, y=-8.
(1)求这个一次函数的关系式和自变量x的取值范围;
(2)当x=5时函数y的值;
(3)当y=4时自变量x的值?
练一练
5.已知y+30与x+5成正比例,且当x=10时,y=60.求y关于x的函数解析式.
练一练
6.已知y+m与x-1成正比例,当x=-1时,y=-15;当x=7时,y=1.求:
(2)当-3<y<7时,自变量x的取值范围;
(1)y关于x的函数解析式;
练一练
7. 在弹性限度内,弹簧的长度y(厘米)是所挂物 体质量x (千克)的一次函数.一根弹簧不挂物体时长14.5厘米;当所挂物体的质量为3千克时,弹簧长16厘米.写出y与x之间的关系式,并求当所挂物体的质量为4千克时弹簧的长度.
练一练
8.按拖拉机的油箱最多可装油56kg,犁地时平均每小时耗油6kg,现装满油后去犁地.
(1)写出油箱中剩余油Q(kg)与犁地时间t(时)之间的函数关系.
(2)求函数自变量的取值范围.
(3)求拖拉机工作4时30分后,油箱中剩多少千克油?
随 堂 作 业
拓展提高
9.很多城市的出租车按里程收费:在一定的里程内按定额收费(起步价),超出规定里程部分按与超出里程成正比例收费.某市出租车的起步价里程为4km,起步价为10元(不计等待时间)
(1)小明一次在该市乘车,从计费表上看到乘车里程和车费分别为6km,14.00元,请用函数解析式表示出租车超出起步价里程时的计费方法;
(2)如果你在该市乘坐出租车的里程为3km,那么需付多少车费?如果乘车里程为8km呢?
10.按近几年,我国经济快速发展,电力需求最大,供应不足,某市为了鼓励居民节约用电,对居民用电收费采取了价格浮动政策;每户居民每月用电不超过20度时,每度电费0.5元;超过20度时,超过部分每度电费0.6元.该市民王先生家七月份用电x度.
(1)求王先生家应付电费y元与用电量x之间的函数解析式.
(2)若王先生家该月用电80度,求他需付的电费;
(3)若王先生家该月付电费22元,求他家该月的用电量;
拓展提高
小结
用待定系数法求一次函数解析式的一般步骤:
1.设:
所求的一次函数解析式为y=kx+b;
2.列:
依已知列出关于k、b的方程组;
3.解:
解方程组,求得k、b;
4.答:
把k、b的值代入y=kx+b ,就得到所求的一次函数解析式.
再见
5.3 一次函数(2)
浙教版《数学》八年级上册
教学目标
1.通过实例进一步加深对一次函数的认识;
2.会用待定系数法求一次函数的解析式,掌握待定系数法的一般步骤;
3.会通过已知自变量的值求相应的一次函数的值,会运用已知一次函数的值求相应自变量的值解决一些简单的实际问题.
通过对求一次函数解析式的方法的学习,培养学生分析问题、解决问题的能力.
能用待定系数法求一次函数的解析式.
知识目标
能力目标
情感目标
知识回顾
1.一次函数与正比例函数:
函数y=kx+b(k,b都是常数,且k≠0)叫做一次函数,
当b=0时,y=kx为正比例函数.
正比例函数是一次函数的特殊形式,
一次函数包括正比例函数.
2.一次函数与正比例函数的关系:
新课引入
(2)若x=1,y=5,则函数关系式_________.
1.已知正比例函数y=kx(k≠0)
y=5x
2.若y与x成正比例,且当x=0.5时,y=3,则y与x的关系式为_________.
y=6x
y=-x
1
3
(1)若比例系数为- , 则函数关系式为_________;
1
3
确定正比例函数的表达式需要一个条件.
新课引入
3.已知一次函数y=kx+1,在x=2时,y=-3,则k=______.
4.若一次函数y=kx+b,当x=-1时,y=2;当x=3时,y=-2.则k=______,b=______.
-1
1
确定一次例函数的表达式需要两个条件.
-2
新课讲解
y=kx
y=kx+b
待确定
待确定
待确定
解一元一次方程
解二元一次方程组
正比例函数
一次函数
知道一对x, y值,可确定k.
知道两对x, y值,可确定k, b.
这种求函数表达式的方法叫做待定系数法.
新课讲解
用待定系数法求一次函数解析式的一般步骤:
1.设:
所求的一次函数解析式为y=kx+b;
2.列:
依已知列出关于k、b的方程组;
3.解:
解方程组,求得k、b;
4.答:
把k、b的值代入y=kx+b ,就得到所求的一次函数解析式.
例3 已知y是x的一次函数,当x=3时,y=1;
当x=-2时,y=-14 .求这个一次函数的关系式.
因为y是x的一次函数,所以可设所求表达
式为y=kx+b,
3k+b=1
-2k+b=-14
解得:k=3,b=-8
解:
将x=3,y=1和x=-2,y=-14分别代入上式,得
所以所求的一次函数表达式为y=3x-8.
例题讲解
做一做
1.已知y是x的一次函数,当x=-4时,y=9; x=6时,y=-1,
(1)求这个一次函数的关系式,自变量x的取值范围;
(2)当x= 时,求函数y的值;
(3)当y=7时,求自变量x的值;
(4)当y<1时,自变量x的取值范围.
做一做
2.已知y-100与x成正比例关系,且当x=10时,y=600.求y关于x的函数解析式
做一做
3.已知y+1与2x-3成正比例
(1)y是x的一次函数吗?
(2)当y=-15时,x=-1 ;当x=7时,y=1,求y关于x的一次函数解析式.
例题讲解
例4 从1995年底开始,某地区的沙漠面积几乎每年以相同的速度增长.据有关报道,到2001年底,该地区的沙漠面积已从1998年底的100.6万公顷扩展到101.2万公顷.
(1)可选用什么数学方法来描述该地区的沙漠面积的变化?
解:
(1)设95年年底沙漠面积为b万公顷,沙漠面积每年
增加k万公顷,经过x年沙漠面积为y万公顷,由题意得
y=kx+b
把x=3时,y=100.6;x=6时,y=101.2分别代入y=kx+b,得
100.6=3k+b
101.2=6k+b
解得
k=0.2
b=100
∴该地区的沙漠面积的变化由一次函数y=0.2x+100来进行描述
例题讲解
例4 从1995年底开始,某地区的沙漠面积几乎每年以相同的速度增长.据有关报道,到2001年底,该地区的沙漠面积已从1998年底的100.6万公顷扩展到101.2万公顷.
(2)如果该地区的沙漠化得不到治理,那么到2020年底,该地区的沙漠面积将增加到多少公顷?
解:
把x=25代入y=0.2x+100,得
y=0.2×25+100
=5+100
=105(万公顷)
如果该地区的沙漠化得不到治理,那么到2020年底,该地区的沙漠面积将增加到105万公顷
练一练
4.已知y是x一次函数,当x=-2时, y=7;当x=3时, y=-8.
(1)求这个一次函数的关系式和自变量x的取值范围;
(2)当x=5时函数y的值;
(3)当y=4时自变量x的值?
练一练
5.已知y+30与x+5成正比例,且当x=10时,y=60.求y关于x的函数解析式.
练一练
6.已知y+m与x-1成正比例,当x=-1时,y=-15;当x=7时,y=1.求:
(2)当-3<y<7时,自变量x的取值范围;
(1)y关于x的函数解析式;
练一练
7. 在弹性限度内,弹簧的长度y(厘米)是所挂物 体质量x (千克)的一次函数.一根弹簧不挂物体时长14.5厘米;当所挂物体的质量为3千克时,弹簧长16厘米.写出y与x之间的关系式,并求当所挂物体的质量为4千克时弹簧的长度.
练一练
8.按拖拉机的油箱最多可装油56kg,犁地时平均每小时耗油6kg,现装满油后去犁地.
(1)写出油箱中剩余油Q(kg)与犁地时间t(时)之间的函数关系.
(2)求函数自变量的取值范围.
(3)求拖拉机工作4时30分后,油箱中剩多少千克油?
随 堂 作 业
拓展提高
9.很多城市的出租车按里程收费:在一定的里程内按定额收费(起步价),超出规定里程部分按与超出里程成正比例收费.某市出租车的起步价里程为4km,起步价为10元(不计等待时间)
(1)小明一次在该市乘车,从计费表上看到乘车里程和车费分别为6km,14.00元,请用函数解析式表示出租车超出起步价里程时的计费方法;
(2)如果你在该市乘坐出租车的里程为3km,那么需付多少车费?如果乘车里程为8km呢?
10.按近几年,我国经济快速发展,电力需求最大,供应不足,某市为了鼓励居民节约用电,对居民用电收费采取了价格浮动政策;每户居民每月用电不超过20度时,每度电费0.5元;超过20度时,超过部分每度电费0.6元.该市民王先生家七月份用电x度.
(1)求王先生家应付电费y元与用电量x之间的函数解析式.
(2)若王先生家该月用电80度,求他需付的电费;
(3)若王先生家该月付电费22元,求他家该月的用电量;
拓展提高
小结
用待定系数法求一次函数解析式的一般步骤:
1.设:
所求的一次函数解析式为y=kx+b;
2.列:
依已知列出关于k、b的方程组;
3.解:
解方程组,求得k、b;
4.答:
把k、b的值代入y=kx+b ,就得到所求的一次函数解析式.
再见
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
