浙教版八年级上册5.5一次函数的简单应用(第1课时)(共22张PPT)
文档属性
| 名称 | 浙教版八年级上册5.5一次函数的简单应用(第1课时)(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 264.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 12:10:54 | ||
图片预览








文档简介
(共22张PPT)
5.5 一次函数的简单应用(1)
浙教版《数学》八年级上册
教学目标
1.了解通过实验获得数据,然后根据数据建立一次函数模型的一般过程;
2.会综合运用一次函数的解析式,函数图象以及结合方程(组)等其他数学模型,解决实际问题.
在解决问题的过程中,进一步体会函数来自于实际又服务于实际,增强数学的应用意识.
不断增强分析问题、解决问题的能力,加深领会数形结合的思想方法,发展学生的形象思维能力.
知识目标
能力目标
情感目标
知识回顾
1.一次函数y=kx+b的图象是 __________.
2.作一次函数图象时,只要确定_____个点,
两
图象与x轴的交点坐标是( ),
与y轴的交点坐标是( );
正比例函数图象经过原点( ).
0,b
0,0
,0
一条直线
3.一次函数的性质
对于一次函数y=kx+b(k,b为常数,且k≠0),
当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小.
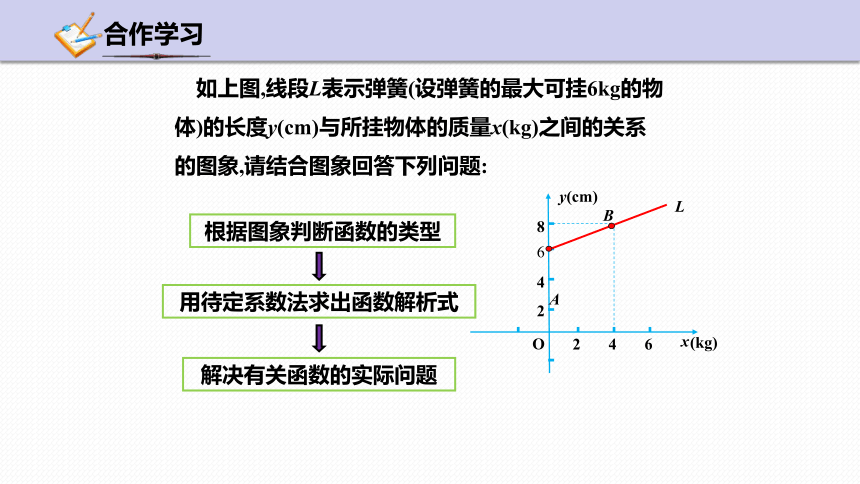
合作学习
x
O
2
4
6
2
(kg)
8
4
6
A
B
L
y(cm)
(1)问题中的两个变量y与x之间是不是一次函数关系
(2)y与x之间的函数关系
是_________________________;
(3)由图知弹簧的原长是______cm.
当x=3时,弹簧的长度y= ______ cm.
是
y=0.5x+6
7.5
6
(0≤x ≤ 6)
如上图,线段L表示弹簧(设弹簧的最大可挂6kg的物体)的长度y(cm)与所挂物体的质量x(kg)之间的关系的图象,请结合图象回答下列问题:
合作学习
x
O
2
4
6
2
(kg)
8
4
6
A
B
L
y(cm)
如上图,线段L表示弹簧(设弹簧的最大可挂6kg的物体)的长度y(cm)与所挂物体的质量x(kg)之间的关系的图象,请结合图象回答下列问题:
根据图象判断函数的类型
用待定系数法求出函数解析式
解决有关函数的实际问题
9
8
7
6
5
0 1 2 3 4 5
x(kg)
变式 弹簧秤上挂上物体后会伸长,测得一弹簧的长度y(cm) 与所挂物体的质量x(kg)有如下关系:
合作学习
x(kg) 0 1 2 3 4 …
y(cm) …
6.0
7.1
7.6
6.4
8.1
请把表格中的点在坐标系中描出来.
根据数据画出函数的图象
近似于一条射线
根据图象判断函数的类型(一次函数)
9
8
7
6
5
0 1 2 3 4 5
x(kg)
合作学习
x(kg) 0 1 2 3 4 …
y(cm) …
6.0
7.1
7.6
6.4
8.1
问:(1)能否用一次函数刻画这两个变量y与x的关系?如果能,请求出这个函数的解析式.
(2)当x=8时, y的值是多少
能
y=0.5x+6
y=10
变式 弹簧秤上挂上物体后会伸长,测得一弹簧的长度y(cm) 与所挂物体的质量x(kg)有如下关系:
9
8
7
6
5
0 1 2 3 4 5
x(kg)
合作学习
x(kg) 0 1 2 3 4 …
y(cm) …
6.0
7.1
7.6
6.4
8.1
寻找数据间的规律
得出函数的解析式
解决有关函数的实际问题
变式 弹簧秤上挂上物体后会伸长,测得一弹簧的长度y(cm) 与所挂物体的质量x(kg)有如下关系:
确定两个变量是否构成一次函数关系的一种常用方法是利用图象去获得经验公式,这种方法的的基本步骤是:
根据图象判断函数的类型
用待定系数法求出函数解析式
解决有关函数的实际问题
新课讲解
通过实验获得数据
根据数据画出函数的图象
根据图象判断函数的类型
用待定系数法求出函数解析式
解决有关函数的实际问题
寻找数据间的规律
得出函数的解析式
运用一次函数的模型解决实际问题过程
(有时是近似的)
新课讲解
例题讲解
例1 生物学家测得7条成熟的雄性鲸的全长y和吻尖到喷水孔的长度x的数据如下表(单位:米):
吻尖到喷水孔的长度x(m ) 1.78 1.91 2.06 2.32 2.59 2.82 2.95
全长y(m) 10 10.25 10.72 11.52 12.5 13.16 13.9
问:能否用一次函数刻画这两个变量x与y的关系?如果能,请求出这个函数的解析式.
x
例题讲解
解:
吻尖到喷水孔的长度x(m ) 1.78 1.91 2.06 2.32 2.59 2.82 2.95
全长y(m) 10 10.25 10.72 11.52 12.5 13.16 13.9
在直角坐标系中画出以表中x的值为横坐标,y的值为纵坐标的七个点.
20
18
16
14
1210
8
6
4
2
0 1 2 3 4 5 x(m)
y(m)
用这样的方法获得的函数有时是近似的!!
例题讲解
解:
在直角坐标系中画出以表中x的值为横坐标,y的值为纵坐标的7个点.
20
18
16
14
1210
8
6
4
2
0 1 2 3 4 5 x(m)
y(m)
7个点几乎在同一直线上,
则所求的函数可以看成是一次函数.
设一次函数为y=kx+b.
把点(1.91,10.25),(2.59,12.50)
代入y=kx+b,得
所以所求的函数解析式为:y=3.31x+3.93
做一做
1.某市出租车计费方法如图所示,请根据图象回答下面的问题:
(3)表示路程s大于3km时,费用y与s之间的关系.
(1)出租车的起步价是多少元?在多少路程内只收起步价?
(2)起步价里程走完之后,每行驶1km需多少车费?
(4)某乘客坐出租车,车费为31元,试求他乘车的路程.
5元
3km
y=2s-1(s>3)
2元
16km
0 3 5 s (km)
y (元)
9
5
新课讲解
关键是识别自变量在不同的取值范围内所对应函数的类型
用待定系数法分别求出不同范围内的函数解析式
分段函数解题思路
练一练
2.如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程随时间变化的图象.根据图象下列结论错误的是( )
A.轮船的速度为20 km/h
B.快艇的速度为40 km/h
C.轮船比快艇先出发2h
D.快艇不能赶上轮船
D
3.经实验检测,不同气温下声音传播的速度如下表所示
(1)能否用一次函数刻画这两个变量x和y的关系?如果能,写出y关于x的函数解析式?
气温x(℃) 0 5 10 15 20
音速y(米/秒) 331 334 337 340 343
(2)当气温x=22 ℃时,小明看到烟花燃放5秒后才听到声响,那么小明与燃放烟花所在地相距多远?
练一练
练一练
4.杭州市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若居民应交水费y(元)与用水量x(吨)的函数关系如图所示.
(1)分别写出0≤x≤15和x>15时,y与x的函数关系式;
(2)若某用户该月用水21吨,
则应交水费多少元?
O
15
20
39.5
27
x(吨)
y(元)
A
B
5.周末小明从家里骑车去超市购物,然后从超市返回家中.小明离家的路程s(km)和所经过的时间t(分)之间的函数关系如图所示,请根据图象回答下列问题:
(1)小明去超市途中的速度是多少?回家途中的速度是多少?
小明在超市逗留了多少时间?
(2)用恰当的方式表示小明回家的路程s(km)和所经过的时间t(分)之间的函数关系.
(3)如图,折线OABC是s与t之间的函数关系的图象,请用函数关系式表示.
2
1
0 10 20 30 40 50 60
t(s)
s(km)
A
C
B
一展身手
6.周末,小明骑自行车从家里出发到野外郊游.从家出发0.5 h后到达甲地,游玩一段时间后按原速前往乙地.小明离家1 h 20 min后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
(1)求小明骑车的速度和在甲地
游玩的时间.
(2)小明从家出发多久后被妈妈
追上?此时离家多远?
(3)若妈妈比小明早10 min到达
乙地,求从小明家到乙地的路程.
一展身手
O
0.5
10
1
x(h)
y(km)
A B
C
E
D
4
3
-
小结
通过实验获得数据
根据数据画出函数的图象
根据图象判断函数的类型
用待定系数法求出函数解析式
解决有关函数的实际问题
寻找数据间的规律
得出函数的解析式
(有时是近似的)
运用一次函数的模型解决实际问题过程
再见
5.5 一次函数的简单应用(1)
浙教版《数学》八年级上册
教学目标
1.了解通过实验获得数据,然后根据数据建立一次函数模型的一般过程;
2.会综合运用一次函数的解析式,函数图象以及结合方程(组)等其他数学模型,解决实际问题.
在解决问题的过程中,进一步体会函数来自于实际又服务于实际,增强数学的应用意识.
不断增强分析问题、解决问题的能力,加深领会数形结合的思想方法,发展学生的形象思维能力.
知识目标
能力目标
情感目标
知识回顾
1.一次函数y=kx+b的图象是 __________.
2.作一次函数图象时,只要确定_____个点,
两
图象与x轴的交点坐标是( ),
与y轴的交点坐标是( );
正比例函数图象经过原点( ).
0,b
0,0
,0
一条直线
3.一次函数的性质
对于一次函数y=kx+b(k,b为常数,且k≠0),
当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小.
合作学习
x
O
2
4
6
2
(kg)
8
4
6
A
B
L
y(cm)
(1)问题中的两个变量y与x之间是不是一次函数关系
(2)y与x之间的函数关系
是_________________________;
(3)由图知弹簧的原长是______cm.
当x=3时,弹簧的长度y= ______ cm.
是
y=0.5x+6
7.5
6
(0≤x ≤ 6)
如上图,线段L表示弹簧(设弹簧的最大可挂6kg的物体)的长度y(cm)与所挂物体的质量x(kg)之间的关系的图象,请结合图象回答下列问题:
合作学习
x
O
2
4
6
2
(kg)
8
4
6
A
B
L
y(cm)
如上图,线段L表示弹簧(设弹簧的最大可挂6kg的物体)的长度y(cm)与所挂物体的质量x(kg)之间的关系的图象,请结合图象回答下列问题:
根据图象判断函数的类型
用待定系数法求出函数解析式
解决有关函数的实际问题
9
8
7
6
5
0 1 2 3 4 5
x(kg)
变式 弹簧秤上挂上物体后会伸长,测得一弹簧的长度y(cm) 与所挂物体的质量x(kg)有如下关系:
合作学习
x(kg) 0 1 2 3 4 …
y(cm) …
6.0
7.1
7.6
6.4
8.1
请把表格中的点在坐标系中描出来.
根据数据画出函数的图象
近似于一条射线
根据图象判断函数的类型(一次函数)
9
8
7
6
5
0 1 2 3 4 5
x(kg)
合作学习
x(kg) 0 1 2 3 4 …
y(cm) …
6.0
7.1
7.6
6.4
8.1
问:(1)能否用一次函数刻画这两个变量y与x的关系?如果能,请求出这个函数的解析式.
(2)当x=8时, y的值是多少
能
y=0.5x+6
y=10
变式 弹簧秤上挂上物体后会伸长,测得一弹簧的长度y(cm) 与所挂物体的质量x(kg)有如下关系:
9
8
7
6
5
0 1 2 3 4 5
x(kg)
合作学习
x(kg) 0 1 2 3 4 …
y(cm) …
6.0
7.1
7.6
6.4
8.1
寻找数据间的规律
得出函数的解析式
解决有关函数的实际问题
变式 弹簧秤上挂上物体后会伸长,测得一弹簧的长度y(cm) 与所挂物体的质量x(kg)有如下关系:
确定两个变量是否构成一次函数关系的一种常用方法是利用图象去获得经验公式,这种方法的的基本步骤是:
根据图象判断函数的类型
用待定系数法求出函数解析式
解决有关函数的实际问题
新课讲解
通过实验获得数据
根据数据画出函数的图象
根据图象判断函数的类型
用待定系数法求出函数解析式
解决有关函数的实际问题
寻找数据间的规律
得出函数的解析式
运用一次函数的模型解决实际问题过程
(有时是近似的)
新课讲解
例题讲解
例1 生物学家测得7条成熟的雄性鲸的全长y和吻尖到喷水孔的长度x的数据如下表(单位:米):
吻尖到喷水孔的长度x(m ) 1.78 1.91 2.06 2.32 2.59 2.82 2.95
全长y(m) 10 10.25 10.72 11.52 12.5 13.16 13.9
问:能否用一次函数刻画这两个变量x与y的关系?如果能,请求出这个函数的解析式.
x
例题讲解
解:
吻尖到喷水孔的长度x(m ) 1.78 1.91 2.06 2.32 2.59 2.82 2.95
全长y(m) 10 10.25 10.72 11.52 12.5 13.16 13.9
在直角坐标系中画出以表中x的值为横坐标,y的值为纵坐标的七个点.
20
18
16
14
1210
8
6
4
2
0 1 2 3 4 5 x(m)
y(m)
用这样的方法获得的函数有时是近似的!!
例题讲解
解:
在直角坐标系中画出以表中x的值为横坐标,y的值为纵坐标的7个点.
20
18
16
14
1210
8
6
4
2
0 1 2 3 4 5 x(m)
y(m)
7个点几乎在同一直线上,
则所求的函数可以看成是一次函数.
设一次函数为y=kx+b.
把点(1.91,10.25),(2.59,12.50)
代入y=kx+b,得
所以所求的函数解析式为:y=3.31x+3.93
做一做
1.某市出租车计费方法如图所示,请根据图象回答下面的问题:
(3)表示路程s大于3km时,费用y与s之间的关系.
(1)出租车的起步价是多少元?在多少路程内只收起步价?
(2)起步价里程走完之后,每行驶1km需多少车费?
(4)某乘客坐出租车,车费为31元,试求他乘车的路程.
5元
3km
y=2s-1(s>3)
2元
16km
0 3 5 s (km)
y (元)
9
5
新课讲解
关键是识别自变量在不同的取值范围内所对应函数的类型
用待定系数法分别求出不同范围内的函数解析式
分段函数解题思路
练一练
2.如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程随时间变化的图象.根据图象下列结论错误的是( )
A.轮船的速度为20 km/h
B.快艇的速度为40 km/h
C.轮船比快艇先出发2h
D.快艇不能赶上轮船
D
3.经实验检测,不同气温下声音传播的速度如下表所示
(1)能否用一次函数刻画这两个变量x和y的关系?如果能,写出y关于x的函数解析式?
气温x(℃) 0 5 10 15 20
音速y(米/秒) 331 334 337 340 343
(2)当气温x=22 ℃时,小明看到烟花燃放5秒后才听到声响,那么小明与燃放烟花所在地相距多远?
练一练
练一练
4.杭州市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若居民应交水费y(元)与用水量x(吨)的函数关系如图所示.
(1)分别写出0≤x≤15和x>15时,y与x的函数关系式;
(2)若某用户该月用水21吨,
则应交水费多少元?
O
15
20
39.5
27
x(吨)
y(元)
A
B
5.周末小明从家里骑车去超市购物,然后从超市返回家中.小明离家的路程s(km)和所经过的时间t(分)之间的函数关系如图所示,请根据图象回答下列问题:
(1)小明去超市途中的速度是多少?回家途中的速度是多少?
小明在超市逗留了多少时间?
(2)用恰当的方式表示小明回家的路程s(km)和所经过的时间t(分)之间的函数关系.
(3)如图,折线OABC是s与t之间的函数关系的图象,请用函数关系式表示.
2
1
0 10 20 30 40 50 60
t(s)
s(km)
A
C
B
一展身手
6.周末,小明骑自行车从家里出发到野外郊游.从家出发0.5 h后到达甲地,游玩一段时间后按原速前往乙地.小明离家1 h 20 min后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
(1)求小明骑车的速度和在甲地
游玩的时间.
(2)小明从家出发多久后被妈妈
追上?此时离家多远?
(3)若妈妈比小明早10 min到达
乙地,求从小明家到乙地的路程.
一展身手
O
0.5
10
1
x(h)
y(km)
A B
C
E
D
4
3
-
小结
通过实验获得数据
根据数据画出函数的图象
根据图象判断函数的类型
用待定系数法求出函数解析式
解决有关函数的实际问题
寻找数据间的规律
得出函数的解析式
(有时是近似的)
运用一次函数的模型解决实际问题过程
再见
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
