浙教版数学八年级上册1.1认识三角形 第2课时 课件(共24张PPT)
文档属性
| 名称 | 浙教版数学八年级上册1.1认识三角形 第2课时 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 308.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 12:21:00 | ||
图片预览







文档简介
(共24张PPT)
1.1 认识三角形(二)
浙教版《数学》八年级上册
教学目标
1.了解三角形的角平分线、中线、高线的概念;
2.会利用量角器、刻度尺画三角形的角平分线、中线、和高线;
3.会利用三角形的角平分线、中线和高的性质,解决有关角度、面积计算等问题.
培养学生形成观察辨别、全面分析、归纳概括等数学方法,培养学生的思维方法和良好的思维品质.
通过新旧知识的认知冲突,激发学生的求知欲,树立知识来源于实践、又服务于实践的观点.
知识目标
能力目标
情感目标
知识回顾
由不在同一直线上的三条线段,首尾顺次相接所组成的图形叫做三角形.
三角形任何两边的和大于第三边.
两边之差<第三边<两边之和
1.怎样的图像叫做三角形?
2. 三角形有哪两个性质?
三角形任何两边的差小于第三边.
新课引入
从一个角的顶点引出的一条射线,把这个角分成两个相等的角.这条射线叫做这个角的平分线.
角平分线的定义:
C
O
B
A
记作:∠AOC=∠BOC= ∠AOB.
用量角器或折纸的方法
用什么方法可以作出角的角平分线呢?
新课引入
任意剪一张三角形纸片ABC,把内角∠BAC对折一次,使AB与AC重合,得到一条折痕AD.把三角形纸片展开、铺平.AD一定平分∠ BAC吗?
A
B
C
D
你能用同样的方法画出或折出任意一个三角形的一个内角的平分线吗
新课引入
A
B
C
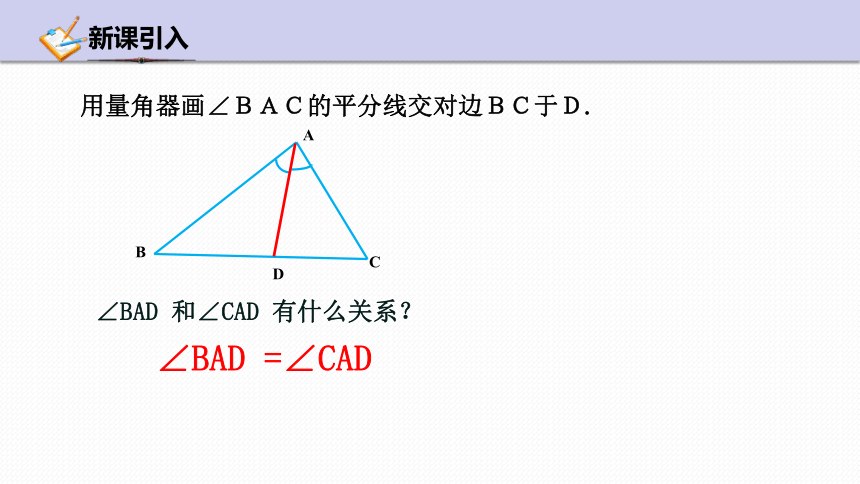
D
∠BAD 和∠CAD 有什么关系?
∠BAD =∠CAD
用量角器画∠BAC的平分线交对边BC于D.
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
三角形的角平分线
∵ AD是 △ ABC的角平分线
∴∠BAD =∠CAD = ∠BAC
1
2
D
A
B
C
如图∠BAC的平分线交BC于点D,线段AD就是△ABC的一条角平分线.
新课讲解
新课讲解
三角形的角平分线与角的平分线有什么区别和联系?
三角形的角平分线仍具有角平分线的基本性质.
思考
区别
联系
1.三角形的角平分线是指三角形三个内角的平分线,角的平分线是指任意角的平分线.
2.三角形的角平分线是一条线段,
角的平分线是一条射线.
新课讲解
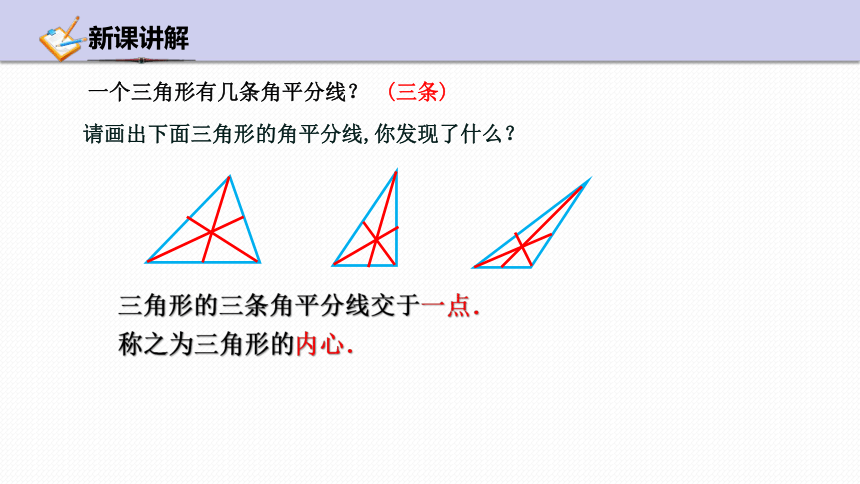
请画出下面三角形的角平分线,你发现了什么?
三角形的三条角平分线交于一点.
一个三角形有几条角平分线?
(三条)
称之为三角形的内心.
做一做
如图,AE是△ABC的角平分线.已知∠B=45°, ∠ C=60°,求下列角的大小.
(1) ∠BAE
C
A
B
E
(1)∵AE是△ABC的角平分线
∵ ∠BAC+∠B+∠C=1800
∴∠CAE=∠BAE= ∠BAC
( )
∴∠BAC=180°-∠B-∠C=1800-450-600=750
∴∠BAE=37.50
(2)∵∠AEB=∠CAE+∠C
∠CAE=∠BAE=37.50
∴∠AEB=37.50+600=97.50
(2) ∠AEB
( )
三角形的内角和定理
三角形的一个外角等于和它不相邻的两个内角的和
解:
D
B
A
C
任意画一个三角形,用刻度尺画BC的中点D,连接AD.
在三角形中,连接一个顶点与它对边中点的线段,叫做三角形的中线.
如图,D为BC的中点,
线段AD就是ΔABC的BC边上的中线.
三角形中线
∵AD是△ ABC的 中线
∴BD = CD = BC
1
2
新课讲解
新课讲解
请画出下面三角形的中线,你发现了什么?
三角形的三条中线交于一点.
一个三角形的中线共有几条?
(三条)
称之为三角形的重心.
如图,AF是ΔABC的角平分线,AE是BC边上的中线,选择“>”、“<”或“=”号填空:
F
E
B
A
(1)BE___EC
(2)∠CAF___―∠BAC
1
2
(3)∠AFB___∠C+∠FAB
(4)∠AEC___∠B
=
=
=
>
C
做一做
三角形的高线
新课讲解
A
B
C
从三角形的一个顶点
向它的对边
所在直线作垂线,
顶点
和垂足
之间的线段
叫做三角形的高线,
简称三角形的高.
如图, 线段AD是BC边上的高.
D
∵ AD是△ ABC的BC边上的高
∴ AD ⊥ BC
新课讲解
请画出下面三角形的高线,你发现了什么?
一个三角形的高线共有几条?
(三条)
A
B
C
D
E
F
A
B
C
D
A
B
C
E
F
D
总结:夹钝角的两边上的高在三角形的外部.因此必须先把它们的边延长,再画它们的高.
新课讲解
高 锐角三角形 直角三角形 钝角三角形
条数
位置
垂足
交点
图形
A
B
C
P
Q
R
3
3
3
都在三角形
内部
直角边上的高分别与另一条直角边重合,还有一条高在三角形内部
夹钝角两边上的高在三角形外部,另一条高在内部
在相应顶点的对边上
①是直角的顶点
②在斜边上
①在相应顶点的对边的延长线上
②在钝角的对边上
在三角形内部
在直角顶点
在三角形外部
总结
三角形的高线
D
E
F
例2 如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线.已知∠BAC=82°,∠C=40°,求∠DAE的大小.
E
D
C
B
A
解:
∵ AE是△ABC的角平分线,且∠BAC=80°,
∵ AD是ABC的高
根据“三角形三个内角的和等于180°”,知
∴ ∠EAC= ∠BAC=40°,
∴ ∠ADC=90°,
∠DAC+ ∠ADC + ∠C =180°,
∴∠DAC=180°-∠ADC -∠C
=180°- 90°-40°=50°
∴∠DAE=∠DAC -∠EAC=50°- 40°=10°
例题讲解
2. 如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
1.下列各组图形中,哪一组图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A.
B.
C.
D.
B
D
做一做
(1)当∠ABC=60°,∠ACB=80°时,求∠BOC的度数.
(2)当∠A=40°时,求∠BOC的度数
(3)当∠A= x 时,求∠BOC的度数
(用含x代数式表示).
3.如图,已知:△ABC中,BD、CE分别是△ABC的两条角平分线,相交于点O
变式:将上体中的角平分线改为高线,∠BOC和∠A又会有什么数量关系?
做一做
A
D
C
B
E
O
4.如图,已知:△ABC中,BD、CE分别是△ABC的两条高线,AC=4,BD=5,CE=3,求AB.
做一做
5.课本P9,探究活动
变式:如图,△ABC的面积为S,D、E、F都是中点,求阴影部分的面积.
B
D
F
E
A
C
F
E
D
A
B
C
三角形的中线可以把三角形分成面积相等的两部分.
一展身手
将这块三角形煎饼分成大小相同的6块,有几种分法?如果限定只能切三刀呢?
一展身手
小结
三角形的 重要线段 概念 图形 表示法
三角形的 角平分线
三角形 的中线
三角形 的高线
∵AD是△ABC的BC上的高线.
∴AD⊥BC
∠ADB=∠ADC=90°.
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段
三角形中,连结一个顶点和它对边中的线段
三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段
∵ AD是△ABC的BC上的中线.
∴ BD=CD= BC.
∵AD是△ABC的∠BAC的平分线
∴ ∠1=∠2= ∠BAC
1.三角形的角平分线、中线和高线
1
2
1
2
再见
1.1 认识三角形(二)
浙教版《数学》八年级上册
教学目标
1.了解三角形的角平分线、中线、高线的概念;
2.会利用量角器、刻度尺画三角形的角平分线、中线、和高线;
3.会利用三角形的角平分线、中线和高的性质,解决有关角度、面积计算等问题.
培养学生形成观察辨别、全面分析、归纳概括等数学方法,培养学生的思维方法和良好的思维品质.
通过新旧知识的认知冲突,激发学生的求知欲,树立知识来源于实践、又服务于实践的观点.
知识目标
能力目标
情感目标
知识回顾
由不在同一直线上的三条线段,首尾顺次相接所组成的图形叫做三角形.
三角形任何两边的和大于第三边.
两边之差<第三边<两边之和
1.怎样的图像叫做三角形?
2. 三角形有哪两个性质?
三角形任何两边的差小于第三边.
新课引入
从一个角的顶点引出的一条射线,把这个角分成两个相等的角.这条射线叫做这个角的平分线.
角平分线的定义:
C
O
B
A
记作:∠AOC=∠BOC= ∠AOB.
用量角器或折纸的方法
用什么方法可以作出角的角平分线呢?
新课引入
任意剪一张三角形纸片ABC,把内角∠BAC对折一次,使AB与AC重合,得到一条折痕AD.把三角形纸片展开、铺平.AD一定平分∠ BAC吗?
A
B
C
D
你能用同样的方法画出或折出任意一个三角形的一个内角的平分线吗
新课引入
A
B
C
D
∠BAD 和∠CAD 有什么关系?
∠BAD =∠CAD
用量角器画∠BAC的平分线交对边BC于D.
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
三角形的角平分线
∵ AD是 △ ABC的角平分线
∴∠BAD =∠CAD = ∠BAC
1
2
D
A
B
C
如图∠BAC的平分线交BC于点D,线段AD就是△ABC的一条角平分线.
新课讲解
新课讲解
三角形的角平分线与角的平分线有什么区别和联系?
三角形的角平分线仍具有角平分线的基本性质.
思考
区别
联系
1.三角形的角平分线是指三角形三个内角的平分线,角的平分线是指任意角的平分线.
2.三角形的角平分线是一条线段,
角的平分线是一条射线.
新课讲解
请画出下面三角形的角平分线,你发现了什么?
三角形的三条角平分线交于一点.
一个三角形有几条角平分线?
(三条)
称之为三角形的内心.
做一做
如图,AE是△ABC的角平分线.已知∠B=45°, ∠ C=60°,求下列角的大小.
(1) ∠BAE
C
A
B
E
(1)∵AE是△ABC的角平分线
∵ ∠BAC+∠B+∠C=1800
∴∠CAE=∠BAE= ∠BAC
( )
∴∠BAC=180°-∠B-∠C=1800-450-600=750
∴∠BAE=37.50
(2)∵∠AEB=∠CAE+∠C
∠CAE=∠BAE=37.50
∴∠AEB=37.50+600=97.50
(2) ∠AEB
( )
三角形的内角和定理
三角形的一个外角等于和它不相邻的两个内角的和
解:
D
B
A
C
任意画一个三角形,用刻度尺画BC的中点D,连接AD.
在三角形中,连接一个顶点与它对边中点的线段,叫做三角形的中线.
如图,D为BC的中点,
线段AD就是ΔABC的BC边上的中线.
三角形中线
∵AD是△ ABC的 中线
∴BD = CD = BC
1
2
新课讲解
新课讲解
请画出下面三角形的中线,你发现了什么?
三角形的三条中线交于一点.
一个三角形的中线共有几条?
(三条)
称之为三角形的重心.
如图,AF是ΔABC的角平分线,AE是BC边上的中线,选择“>”、“<”或“=”号填空:
F
E
B
A
(1)BE___EC
(2)∠CAF___―∠BAC
1
2
(3)∠AFB___∠C+∠FAB
(4)∠AEC___∠B
=
=
=
>
C
做一做
三角形的高线
新课讲解
A
B
C
从三角形的一个顶点
向它的对边
所在直线作垂线,
顶点
和垂足
之间的线段
叫做三角形的高线,
简称三角形的高.
如图, 线段AD是BC边上的高.
D
∵ AD是△ ABC的BC边上的高
∴ AD ⊥ BC
新课讲解
请画出下面三角形的高线,你发现了什么?
一个三角形的高线共有几条?
(三条)
A
B
C
D
E
F
A
B
C
D
A
B
C
E
F
D
总结:夹钝角的两边上的高在三角形的外部.因此必须先把它们的边延长,再画它们的高.
新课讲解
高 锐角三角形 直角三角形 钝角三角形
条数
位置
垂足
交点
图形
A
B
C
P
Q
R
3
3
3
都在三角形
内部
直角边上的高分别与另一条直角边重合,还有一条高在三角形内部
夹钝角两边上的高在三角形外部,另一条高在内部
在相应顶点的对边上
①是直角的顶点
②在斜边上
①在相应顶点的对边的延长线上
②在钝角的对边上
在三角形内部
在直角顶点
在三角形外部
总结
三角形的高线
D
E
F
例2 如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线.已知∠BAC=82°,∠C=40°,求∠DAE的大小.
E
D
C
B
A
解:
∵ AE是△ABC的角平分线,且∠BAC=80°,
∵ AD是ABC的高
根据“三角形三个内角的和等于180°”,知
∴ ∠EAC= ∠BAC=40°,
∴ ∠ADC=90°,
∠DAC+ ∠ADC + ∠C =180°,
∴∠DAC=180°-∠ADC -∠C
=180°- 90°-40°=50°
∴∠DAE=∠DAC -∠EAC=50°- 40°=10°
例题讲解
2. 如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
1.下列各组图形中,哪一组图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A.
B.
C.
D.
B
D
做一做
(1)当∠ABC=60°,∠ACB=80°时,求∠BOC的度数.
(2)当∠A=40°时,求∠BOC的度数
(3)当∠A= x 时,求∠BOC的度数
(用含x代数式表示).
3.如图,已知:△ABC中,BD、CE分别是△ABC的两条角平分线,相交于点O
变式:将上体中的角平分线改为高线,∠BOC和∠A又会有什么数量关系?
做一做
A
D
C
B
E
O
4.如图,已知:△ABC中,BD、CE分别是△ABC的两条高线,AC=4,BD=5,CE=3,求AB.
做一做
5.课本P9,探究活动
变式:如图,△ABC的面积为S,D、E、F都是中点,求阴影部分的面积.
B
D
F
E
A
C
F
E
D
A
B
C
三角形的中线可以把三角形分成面积相等的两部分.
一展身手
将这块三角形煎饼分成大小相同的6块,有几种分法?如果限定只能切三刀呢?
一展身手
小结
三角形的 重要线段 概念 图形 表示法
三角形的 角平分线
三角形 的中线
三角形 的高线
∵AD是△ABC的BC上的高线.
∴AD⊥BC
∠ADB=∠ADC=90°.
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段
三角形中,连结一个顶点和它对边中的线段
三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段
∵ AD是△ABC的BC上的中线.
∴ BD=CD= BC.
∵AD是△ABC的∠BAC的平分线
∴ ∠1=∠2= ∠BAC
1.三角形的角平分线、中线和高线
1
2
1
2
再见
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
