浙教版数学八年级上册1.3证明 第1课时 课件(共19张PPT)
文档属性
| 名称 | 浙教版数学八年级上册1.3证明 第1课时 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 185.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 12:23:21 | ||
图片预览



文档简介
(共19张PPT)
1.3 证明(一)
浙教版《数学》八年级上册
教学目标
1.通过观察、分析、猜想、验证等教学活动的过程,使学生理解证明的必要性;
2.了解证明的含义;
3.了解证明的表达式.
会按规定格式证明简单命题,体会证明过程要步步有理有据.
培养学生主动探索、敢于实践、合情推理的意识,养成言必有据的思维习惯.
知识目标
能力目标
情感目标
知识回顾
1.现阶段我们在数学上学习的命题有几类?
命题
真命题
假命题
2.说明一个命题是假命题的方法:
举反例
3.说明一个命题是真命题的方法:
推理
定义
公理
已证明的定理
4.推理的依据:
合作学习
a
b
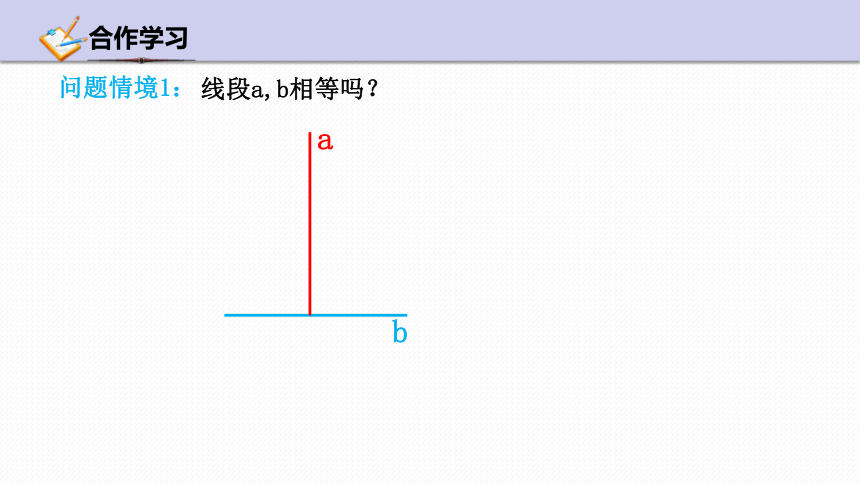
问题情境1:
线段a,b相等吗?
合作学习
a
b
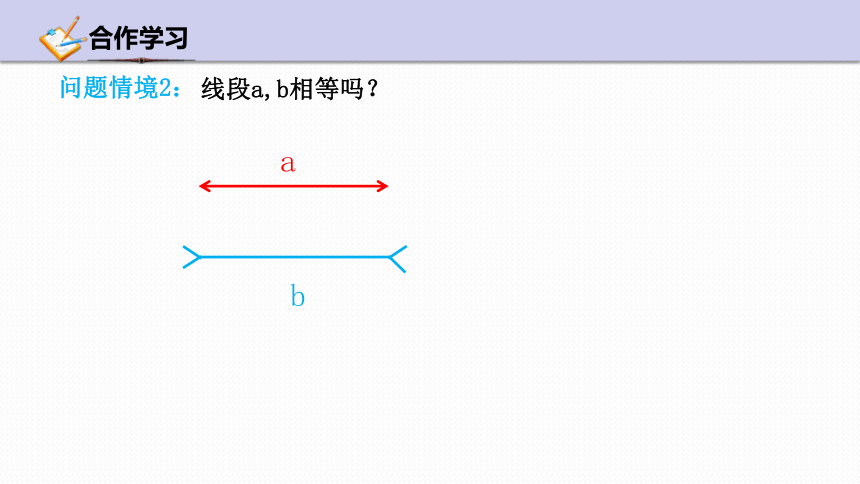
问题情境2:
线段a,b相等吗?
合作学习
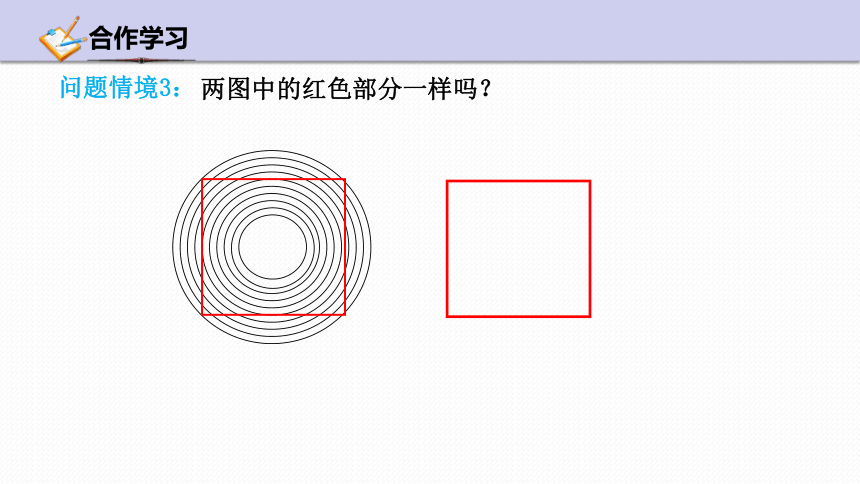
问题情境3:
两图中的红色部分一样吗?
新课讲解
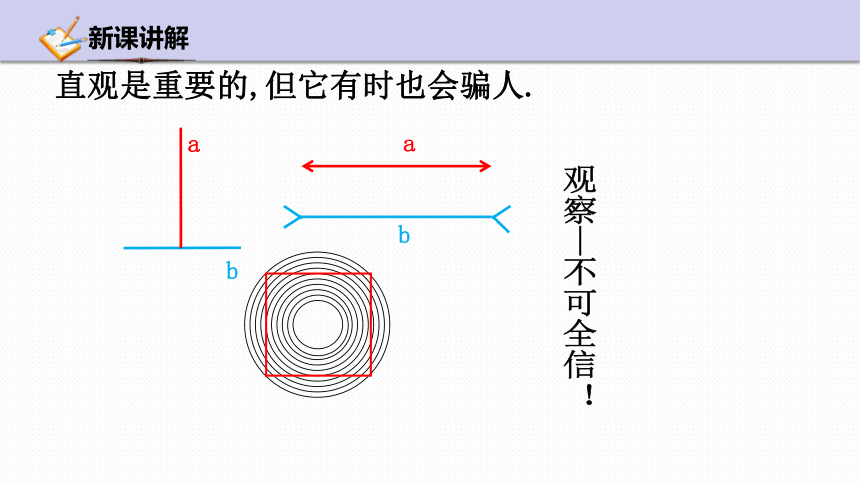
直观是重要的,但它有时也会骗人.
a
b
a
b
观察—不可全信!
合作学习
列举—不够严谨!
当n=6时, n2-3n+7 =25不是质数
当n=0,1,2,3,4时,代数式n2-3n+7的值分别是7,5,5,7,11,它们都是质数.那么,命题“对于自然数n,代数式n2-3n+7的值都是质数”是真命题吗
问题情境4:
如何判断一个命题是真命题?
二、列举
不够严谨!
一、目测(直观)
错觉!
三、测量
存在误差!
通过推理的方式,即根据已知的事实来推断未知事实;
要判定一个命题是真命题,往往需要从命题的条件出发,根据已知的定义、基本事实、定理,一步一步推得结论成立,这样的推理过程叫做证明 。
新课讲解
新课讲解
如图,直线AB与CD被l所截,∠1=∠2
则∠1=∠3
∵∠1=∠2 ( )
∴AB//CD ( )
∴∠1=∠3 ( )
----条件
----结论
已知:
求证:
----图形
理由如下:
证明:
已知
两直线平行,同位角相等
(请说明理由)
几何证明题的构成?
内错角相等,两直线平行
推理
过程
----
C
D
B
A
3
2
1
l
∵∠1=∠2
∴AB//CD
∴∠1=∠3
证明:
(已知)
(两直线平行,同位角相等)
(内错角相等,两直线平行)
根据条件
依据已学
步步递推
证实判断
(步步有据)
新课讲解
证明步骤:
例1 已知:如图DE //BC, ∠ 1=∠E.
求证:BE平分∠ABC.
∵DE //BC ( )
证明:
∴∠2=∠E ( )
已知
两直线平行,内错角相等
∵∠1=∠E ( )
已知
∴∠1=∠2
(由“因”导“果”)
(执“果”索“因”)
证明几何命题的基本思路:
顺推分析
从条件
结论
逆推分析
从结论
条件
例题讲解
D
A
2
1
C
B
E
∠PFE= ∠DFE ( )
1
2
例2 已知:如图,AB //CD,
EP,FP分别平∠BEF,∠DFE.
求证:∠ PEF+∠PFE=90°
∵ EP,FP分别平∠BEF,∠DFE ( )
证明:
已知
两角平分线的定义
∵AB∥CD ( )
已知
∴∠BEF+∠DFE=180°( )
两直线平行,
同旁内角互补
∴∠PEF= ∠BEF
1
2
∴∠PEF+∠PFE= ∠BEF+ ∠DFE
1
2
1
2
= (∠BEF+∠DFE)
1
2
=90°
例题讲解
D
A
C
B
P
F
E
做一做
1. 填空
已知:如图1,∠1=∠2,∠3=∠4,
求证:EG∥FH.
证明:∵∠1=∠2(已知)
∠AEF=∠1 ( );
∴∠AEF=∠2 ( ).
∴AB∥CD ( ).
∴∠BEF=∠CFE ( ).
∵∠3=∠4(已知);
∴∠BEF-∠4=∠CFE-∠3.
即∠GEF=∠HFE ( ).
∴EG∥FH ( ).
对顶角相等
等量代换
同位角相等,两直线平行
两直线平行,内错角相等
等式性质
内错角相等,两直线平行
H
D
A
3
2
1
4
C
B
G
F
E
做一做
2. 已知:如图,直线a,b被直线c所截,AB⊥b, ∠1=∠2
求证:∠1 与∠3互为余角
c
b
a
C
B
A
3
2
1
3. 如图,BC⊥ AC于点C,CD⊥AB于点D,
∠EBC=∠A,
求证:BE∥CD
E
B
A
C
D
做一做
一展身手
4. 命题“若n是自然数,则代数式(3n+1)(3n+2)+1的值是3的倍数”是真命题还是假命题?如果你认为是假命题,请说明理由;如果你认为是真命题,给出证明.
小结
依据思路,运用数学符号和数学语言条理清晰地写出证明过程;检查表达过程是否正确、完善.
证明思路:
由“因”导“果”
执“果”索“因”
⑴ 画:
⑵ 写:
⑶ 证:
(步步有据)
证明步骤:
没有图形的要按题意画出图形
在“已知”中写出“条件”
在“求证”中写出“结论”
分清命题的条件和结论,结合图形,
在“证明”中写出推理过程
再见
1.3 证明(一)
浙教版《数学》八年级上册
教学目标
1.通过观察、分析、猜想、验证等教学活动的过程,使学生理解证明的必要性;
2.了解证明的含义;
3.了解证明的表达式.
会按规定格式证明简单命题,体会证明过程要步步有理有据.
培养学生主动探索、敢于实践、合情推理的意识,养成言必有据的思维习惯.
知识目标
能力目标
情感目标
知识回顾
1.现阶段我们在数学上学习的命题有几类?
命题
真命题
假命题
2.说明一个命题是假命题的方法:
举反例
3.说明一个命题是真命题的方法:
推理
定义
公理
已证明的定理
4.推理的依据:
合作学习
a
b
问题情境1:
线段a,b相等吗?
合作学习
a
b
问题情境2:
线段a,b相等吗?
合作学习
问题情境3:
两图中的红色部分一样吗?
新课讲解
直观是重要的,但它有时也会骗人.
a
b
a
b
观察—不可全信!
合作学习
列举—不够严谨!
当n=6时, n2-3n+7 =25不是质数
当n=0,1,2,3,4时,代数式n2-3n+7的值分别是7,5,5,7,11,它们都是质数.那么,命题“对于自然数n,代数式n2-3n+7的值都是质数”是真命题吗
问题情境4:
如何判断一个命题是真命题?
二、列举
不够严谨!
一、目测(直观)
错觉!
三、测量
存在误差!
通过推理的方式,即根据已知的事实来推断未知事实;
要判定一个命题是真命题,往往需要从命题的条件出发,根据已知的定义、基本事实、定理,一步一步推得结论成立,这样的推理过程叫做证明 。
新课讲解
新课讲解
如图,直线AB与CD被l所截,∠1=∠2
则∠1=∠3
∵∠1=∠2 ( )
∴AB//CD ( )
∴∠1=∠3 ( )
----条件
----结论
已知:
求证:
----图形
理由如下:
证明:
已知
两直线平行,同位角相等
(请说明理由)
几何证明题的构成?
内错角相等,两直线平行
推理
过程
----
C
D
B
A
3
2
1
l
∵∠1=∠2
∴AB//CD
∴∠1=∠3
证明:
(已知)
(两直线平行,同位角相等)
(内错角相等,两直线平行)
根据条件
依据已学
步步递推
证实判断
(步步有据)
新课讲解
证明步骤:
例1 已知:如图DE //BC, ∠ 1=∠E.
求证:BE平分∠ABC.
∵DE //BC ( )
证明:
∴∠2=∠E ( )
已知
两直线平行,内错角相等
∵∠1=∠E ( )
已知
∴∠1=∠2
(由“因”导“果”)
(执“果”索“因”)
证明几何命题的基本思路:
顺推分析
从条件
结论
逆推分析
从结论
条件
例题讲解
D
A
2
1
C
B
E
∠PFE= ∠DFE ( )
1
2
例2 已知:如图,AB //CD,
EP,FP分别平∠BEF,∠DFE.
求证:∠ PEF+∠PFE=90°
∵ EP,FP分别平∠BEF,∠DFE ( )
证明:
已知
两角平分线的定义
∵AB∥CD ( )
已知
∴∠BEF+∠DFE=180°( )
两直线平行,
同旁内角互补
∴∠PEF= ∠BEF
1
2
∴∠PEF+∠PFE= ∠BEF+ ∠DFE
1
2
1
2
= (∠BEF+∠DFE)
1
2
=90°
例题讲解
D
A
C
B
P
F
E
做一做
1. 填空
已知:如图1,∠1=∠2,∠3=∠4,
求证:EG∥FH.
证明:∵∠1=∠2(已知)
∠AEF=∠1 ( );
∴∠AEF=∠2 ( ).
∴AB∥CD ( ).
∴∠BEF=∠CFE ( ).
∵∠3=∠4(已知);
∴∠BEF-∠4=∠CFE-∠3.
即∠GEF=∠HFE ( ).
∴EG∥FH ( ).
对顶角相等
等量代换
同位角相等,两直线平行
两直线平行,内错角相等
等式性质
内错角相等,两直线平行
H
D
A
3
2
1
4
C
B
G
F
E
做一做
2. 已知:如图,直线a,b被直线c所截,AB⊥b, ∠1=∠2
求证:∠1 与∠3互为余角
c
b
a
C
B
A
3
2
1
3. 如图,BC⊥ AC于点C,CD⊥AB于点D,
∠EBC=∠A,
求证:BE∥CD
E
B
A
C
D
做一做
一展身手
4. 命题“若n是自然数,则代数式(3n+1)(3n+2)+1的值是3的倍数”是真命题还是假命题?如果你认为是假命题,请说明理由;如果你认为是真命题,给出证明.
小结
依据思路,运用数学符号和数学语言条理清晰地写出证明过程;检查表达过程是否正确、完善.
证明思路:
由“因”导“果”
执“果”索“因”
⑴ 画:
⑵ 写:
⑶ 证:
(步步有据)
证明步骤:
没有图形的要按题意画出图形
在“已知”中写出“条件”
在“求证”中写出“结论”
分清命题的条件和结论,结合图形,
在“证明”中写出推理过程
再见
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
