浙教版数学八年级上册 1.3证明 第2课时 课件(共19张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 1.3证明 第2课时 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 194.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 12:23:57 | ||
图片预览




文档简介
(共19张PPT)
1.3 证明(二)
浙教版《数学》八年级上册
教学目标
1.探索并理解三角形内角和定理的几何证明;
2.进一步巩固证明的书写格式;
进一步熟悉证明的书写和表达,能完成简单的几何命题的证明.
1.进一步体会证明的含义,从证明过程的言之有理中感悟推理的严密性;
2.体验从实验几何向推理几何的过渡.
知识目标
能力目标
情感目标
依据思路,运用数学符号和数学语言条理清晰地写出证明过程;检查表达过程是否正确、完善.
证明思路:
由“因”导“果”
执“果”索“因”
⑴ 画:
⑵ 写:
⑶ 证:
(步步有据)
证明步骤:
按题意画出图形
在“已知”中写出“条件”
在“求证”中写出“结论”
分清命题的条件和结论,结合图形,
在“证明”中写出推理过程
知识回顾
新课引入
A
B
C
对于三角形,我们已经有哪些认识?
定义
分类
内角和
…………
三角形的三个内角的和等于180°.
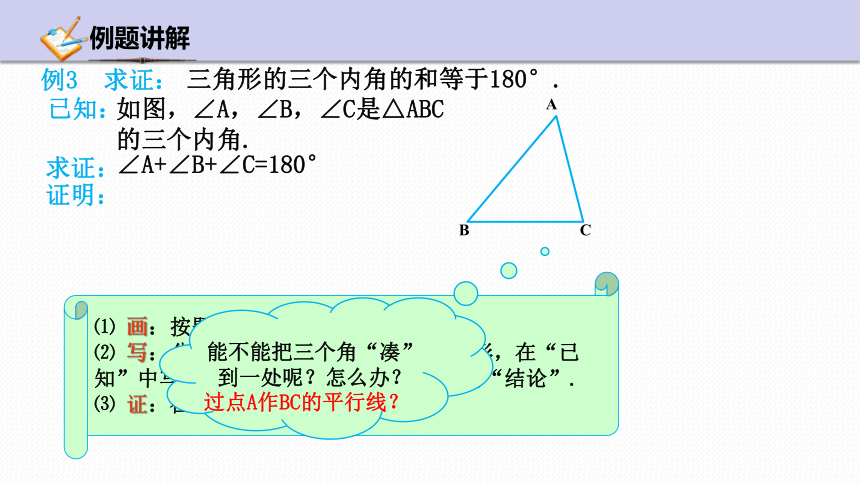
例3 求证:
已知:
求证:
如图,∠A,∠B,∠C是△ABC的三个内角.
∠A+∠B+∠C=180°
⑴ 画:按题意画出图形.
⑵ 写:分清命题的条件和结论,结合图形,在“已知”中写出“条件”,在“求证”中写出“结论”.
⑶ 证:在“证明”中写出推理过程.
证明:
能不能把三个角“凑”到一处呢?怎么办?
过点A作BC的平行线?
A
B
C
例题讲解
A
B
C
=180
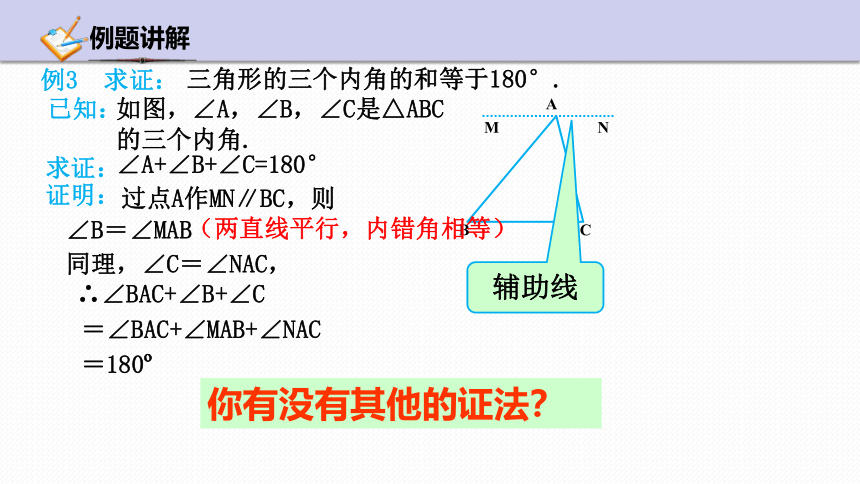
过点A作MN∥BC,则
同理,∠C=∠NAC,
∠B=∠MAB
(两直线平行,内错角相等)
∴∠BAC+∠B+∠C
=∠BAC+∠MAB+∠NAC
你有没有其他的证法?
M
N
辅助线
三角形的三个内角的和等于180°.
例3 求证:
已知:
求证:
如图,∠A,∠B,∠C是△ABC的三个内角.
∠A+∠B+∠C=180°
证明:
例题讲解
E
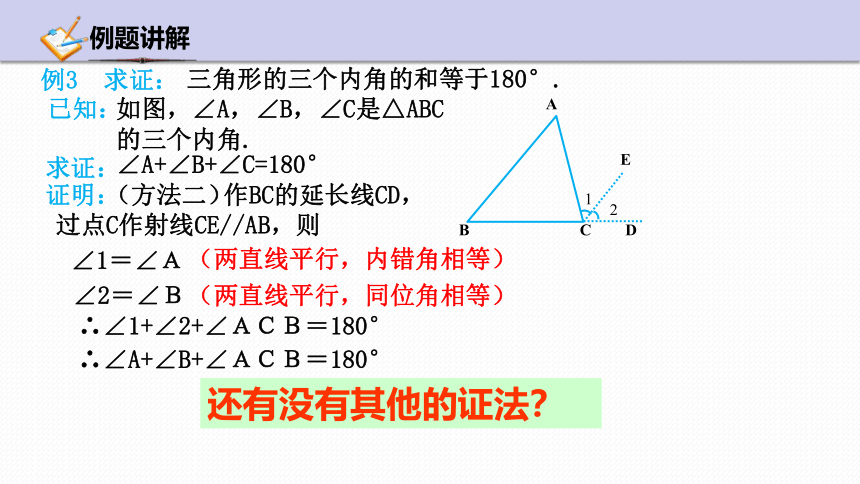
(方法二)
2
1
D
A
B
C
作BC的延长线CD,
过点C作射线CE//AB,则
∠1=∠A
(两直线平行,内错角相等)
∠2=∠B
(两直线平行,同位角相等)
∴∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
三角形的三个内角的和等于180°.
例3 求证:
已知:
求证:
如图,∠A,∠B,∠C是△ABC的三个内角.
∠A+∠B+∠C=180°
证明:
还有没有其他的证法?
例题讲解
A
B
C
E
图1
E
A
B
C
D
F
图2
A
N
B
C
T
S
图3
P
Q
R
M
A
N
B
C
T
S
图4
P
Q
R
M
例题讲解
关于辅助线:
3.添加辅助线,可构造新图形,形成新关系,找到联系已知与未知的桥梁,把问题转化,要根据需要而定,平时做题时要注意总结.
2.它的作用是把分散的条件集中,把隐含的条件显现出来,起到牵线搭桥的作用.
1.辅助线是为了证明需要在原图上添画的线.
(辅助线通常画成虚线)
新课讲解
A
B
C
D
三角形的外角
如图,∠ACD是由△ABC的一条边BC的延长线和另一条相邻的边CA组成的角,这样的角叫做该三角形的外角.
新课讲解
A
B
C
D
∠ACD +∠ACB=180°
∠A+∠B+∠ACB=180°
由图可知
∴∠ACD=∠A+∠B
三角形的外角等于与它不相邻的两个内角的和.
推论1:
∴∠ACD>∠A
∠ACD>∠B
三角形的外角大于任何一个与它不相邻的内角.
推论2:
新课讲解
例4 已知:如图,∠B+∠D=∠BCD,求证:AB∥DE
E
D
A
B
C
F
∴AB∥DE
延长BC,交DE于点F.
又∵∠BCD=∠D+ ∠CFD
∵∠B+∠D=∠BCD
(已知)
∴∠B+∠D=∠D+ ∠CFD
∴∠B=∠CFD
证明:
(三角形的外角等于与它不相邻的两个内角的和)
(内错角相等,两直线平行)
例题讲解
1.已知如图(1): ∠ BAF,∠CBD, ∠ ACE是∠△ABC的三个外角.则∠ BAF+∠CBD+∠ ACE= .
360°
2.如图(2),在△ABC中,以A为顶点的一个外角为120°,∠B=50°,则∠C= °,请说明理由.
70
A
B
C
D
图2
A
B
C
D
E
F
图1
做一做
3.已知:在△ABC中,∠1是它的一个外角, E为边AB上的一点,延长BC到D,连接DE.
求证: ∠1>∠2.
A
B
C
D
E
F
1
2
3
做一做
4.如图 ,把△ABC纸片沿DE折叠,当点A落在四边形DEBC内部时, ∠A与∠1+ ∠2之间存在着一种数量关系,试找出.
一展身手
1
2
B
C
A
A
E
D
5.如图(甲),在五角星图形中,
求:∠A+∠B+∠C+∠D+∠E的度数.
A
B
C
D
E
(甲)
一展身手
把图(乙)、(丙)叫蜕化的五角星,问它们的五角之和与五角星图形的五角之和仍相等吗?
为什么?
变式:
(乙)
E
B
C
A
D
(丙)
C
B
E
D
A
一展身手
小结
1.三角形内角和定理的证明方法
添加辅助线
三角形的三个内角和等于180°.
2.常见的几何证明方法:
分析法
3.三角形的内角和定理:
推论1:
推论2:
三角形的外角等于与它不相邻的两个内角的和.
三角形的外角大于任何一个与它不相邻的内角.
再见
1.3 证明(二)
浙教版《数学》八年级上册
教学目标
1.探索并理解三角形内角和定理的几何证明;
2.进一步巩固证明的书写格式;
进一步熟悉证明的书写和表达,能完成简单的几何命题的证明.
1.进一步体会证明的含义,从证明过程的言之有理中感悟推理的严密性;
2.体验从实验几何向推理几何的过渡.
知识目标
能力目标
情感目标
依据思路,运用数学符号和数学语言条理清晰地写出证明过程;检查表达过程是否正确、完善.
证明思路:
由“因”导“果”
执“果”索“因”
⑴ 画:
⑵ 写:
⑶ 证:
(步步有据)
证明步骤:
按题意画出图形
在“已知”中写出“条件”
在“求证”中写出“结论”
分清命题的条件和结论,结合图形,
在“证明”中写出推理过程
知识回顾
新课引入
A
B
C
对于三角形,我们已经有哪些认识?
定义
分类
内角和
…………
三角形的三个内角的和等于180°.
例3 求证:
已知:
求证:
如图,∠A,∠B,∠C是△ABC的三个内角.
∠A+∠B+∠C=180°
⑴ 画:按题意画出图形.
⑵ 写:分清命题的条件和结论,结合图形,在“已知”中写出“条件”,在“求证”中写出“结论”.
⑶ 证:在“证明”中写出推理过程.
证明:
能不能把三个角“凑”到一处呢?怎么办?
过点A作BC的平行线?
A
B
C
例题讲解
A
B
C
=180
过点A作MN∥BC,则
同理,∠C=∠NAC,
∠B=∠MAB
(两直线平行,内错角相等)
∴∠BAC+∠B+∠C
=∠BAC+∠MAB+∠NAC
你有没有其他的证法?
M
N
辅助线
三角形的三个内角的和等于180°.
例3 求证:
已知:
求证:
如图,∠A,∠B,∠C是△ABC的三个内角.
∠A+∠B+∠C=180°
证明:
例题讲解
E
(方法二)
2
1
D
A
B
C
作BC的延长线CD,
过点C作射线CE//AB,则
∠1=∠A
(两直线平行,内错角相等)
∠2=∠B
(两直线平行,同位角相等)
∴∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
三角形的三个内角的和等于180°.
例3 求证:
已知:
求证:
如图,∠A,∠B,∠C是△ABC的三个内角.
∠A+∠B+∠C=180°
证明:
还有没有其他的证法?
例题讲解
A
B
C
E
图1
E
A
B
C
D
F
图2
A
N
B
C
T
S
图3
P
Q
R
M
A
N
B
C
T
S
图4
P
Q
R
M
例题讲解
关于辅助线:
3.添加辅助线,可构造新图形,形成新关系,找到联系已知与未知的桥梁,把问题转化,要根据需要而定,平时做题时要注意总结.
2.它的作用是把分散的条件集中,把隐含的条件显现出来,起到牵线搭桥的作用.
1.辅助线是为了证明需要在原图上添画的线.
(辅助线通常画成虚线)
新课讲解
A
B
C
D
三角形的外角
如图,∠ACD是由△ABC的一条边BC的延长线和另一条相邻的边CA组成的角,这样的角叫做该三角形的外角.
新课讲解
A
B
C
D
∠ACD +∠ACB=180°
∠A+∠B+∠ACB=180°
由图可知
∴∠ACD=∠A+∠B
三角形的外角等于与它不相邻的两个内角的和.
推论1:
∴∠ACD>∠A
∠ACD>∠B
三角形的外角大于任何一个与它不相邻的内角.
推论2:
新课讲解
例4 已知:如图,∠B+∠D=∠BCD,求证:AB∥DE
E
D
A
B
C
F
∴AB∥DE
延长BC,交DE于点F.
又∵∠BCD=∠D+ ∠CFD
∵∠B+∠D=∠BCD
(已知)
∴∠B+∠D=∠D+ ∠CFD
∴∠B=∠CFD
证明:
(三角形的外角等于与它不相邻的两个内角的和)
(内错角相等,两直线平行)
例题讲解
1.已知如图(1): ∠ BAF,∠CBD, ∠ ACE是∠△ABC的三个外角.则∠ BAF+∠CBD+∠ ACE= .
360°
2.如图(2),在△ABC中,以A为顶点的一个外角为120°,∠B=50°,则∠C= °,请说明理由.
70
A
B
C
D
图2
A
B
C
D
E
F
图1
做一做
3.已知:在△ABC中,∠1是它的一个外角, E为边AB上的一点,延长BC到D,连接DE.
求证: ∠1>∠2.
A
B
C
D
E
F
1
2
3
做一做
4.如图 ,把△ABC纸片沿DE折叠,当点A落在四边形DEBC内部时, ∠A与∠1+ ∠2之间存在着一种数量关系,试找出.
一展身手
1
2
B
C
A
A
E
D
5.如图(甲),在五角星图形中,
求:∠A+∠B+∠C+∠D+∠E的度数.
A
B
C
D
E
(甲)
一展身手
把图(乙)、(丙)叫蜕化的五角星,问它们的五角之和与五角星图形的五角之和仍相等吗?
为什么?
变式:
(乙)
E
B
C
A
D
(丙)
C
B
E
D
A
一展身手
小结
1.三角形内角和定理的证明方法
添加辅助线
三角形的三个内角和等于180°.
2.常见的几何证明方法:
分析法
3.三角形的内角和定理:
推论1:
推论2:
三角形的外角等于与它不相邻的两个内角的和.
三角形的外角大于任何一个与它不相邻的内角.
再见
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
