浙教版数学八年级上册 1.5三角形全等的判定 第3课时 课件(共18张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 1.5三角形全等的判定 第3课时 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 225.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 12:26:44 | ||
图片预览



文档简介
(共18张PPT)
1.5 三角形全等的判定(三)
浙教版《数学》八年级上册
教学目标
1.探索并掌握两个三角形全等的条件:两个角及其夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”);
2.会用ASA判定两个三角形全等;
体会利用转化的数学思想和方法解决问题的过程.
在探索三角形全等条件及其运用的过程中,能够进行有条理的思考并进行简单推理.
知识目标
能力目标
情感目标
知识回顾
1.要判定两个三角形全等我们已经学过几种方法:
① 能完全重合的两个三角形是全等三角形(定义)
② 有三条边对应相等的两个三角形全等(简称SSS)
③ 有两边和它们的夹角对应相等的两个三角形全等(简称SAS)
2.垂直平分线的性质:
线段垂直平分线上的点到线段两端的距离相等.
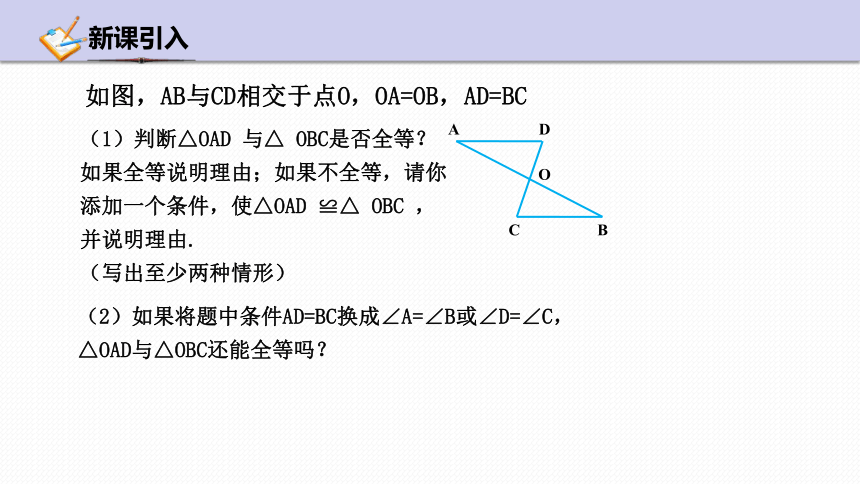
如图,AB与CD相交于点O,OA=OB,AD=BC
(2)如果将题中条件AD=BC换成∠A=∠B或∠D=∠C, △OAD与△OBC还能全等吗?
(1)判断△OAD 与△ OBC是否全等?如果全等说明理由;如果不全等,请你添加一个条件,使△OAD ≌△ OBC ,并说明理由.
(写出至少两种情形)
A
B
C
O
D
新课引入
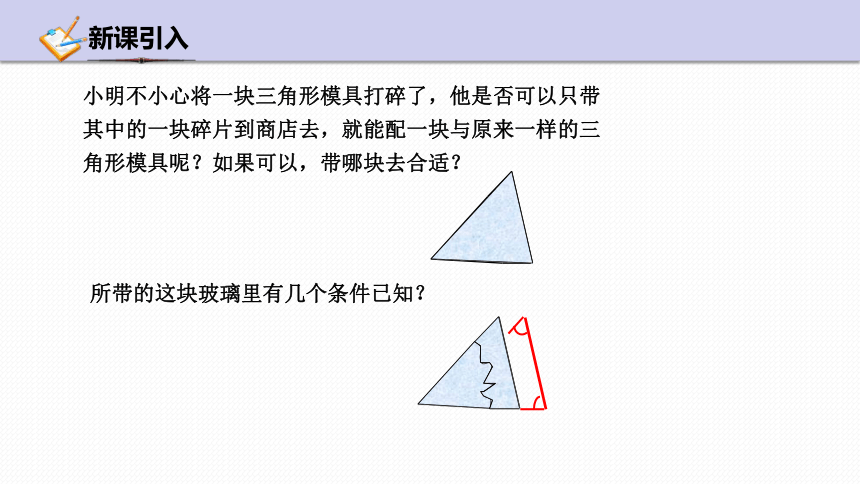
小明不小心将一块三角形模具打碎了,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适?
所带的这块玻璃里有几个条件已知?
新课引入
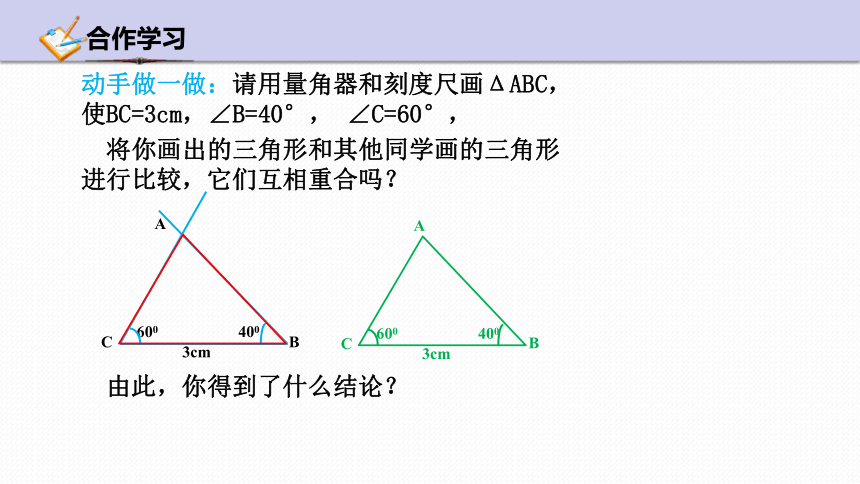
将你画出的三角形和其他同学画的三角形进行比较,它们互相重合吗?
由此,你得到了什么结论?
合作学习
动手做一做:请用量角器和刻度尺画ΔABC,使BC=3cm,∠B=40°, ∠C=60°,
C
B
A
600
400
3cm
B
C
A
600
400
3cm
A
B
C
D
E
F
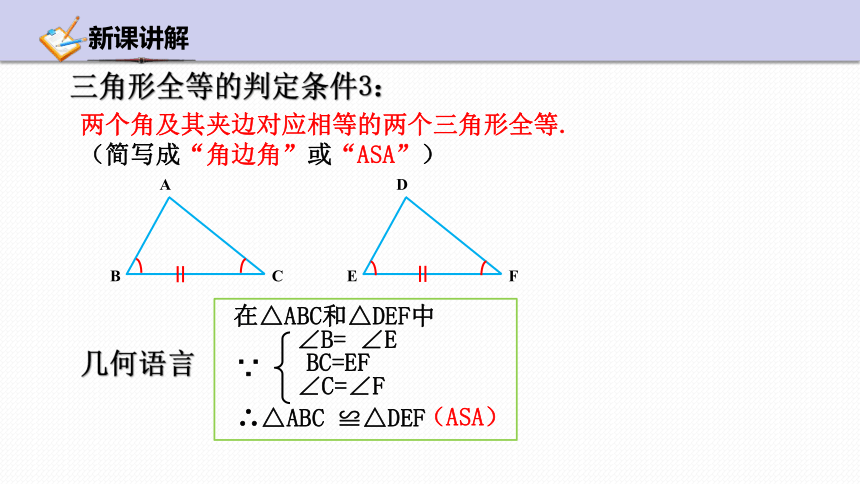
两个角及其夹边对应相等的两个三角形全等.
(简写成“角边角”或“ASA”)
三角形全等的判定条件3:
∴△ABC ≌△DEF
∠B= ∠E
BC=EF
(ASA)
在△ABC和△DEF中
几何语言
∵
新课讲解
∠C=∠F
在△ABC和△DEF中
∠A=∠D
____=____
∠B=∠E
∴ △ABC≌△DEF(ASA)
AB DE
A
B
C
D
E
F
1.填一填
做一做
在△ABC和△DEF中
=__ _
AC=DF
=__ _
∴ △ABC≌△DEF(ASA)
∠A ∠D
∠C ∠F
做一做
A
B
C
D
E
F
1
2
3
4
D
A
B
C
如图,∠1=∠2,∠3=∠4,说明:AC=AD
解:∵∠ =180 -∠3
∠ =180 -∠4
而∠3=∠4(已知)
∴∠ABD=∠ABC
在△ 和△ 中
( )
(公共边)
( )
∴△ ≌ △ ( )
∴ (全等三角形对应边相等)
ABD
ABC
ABC
∠1=∠2
AB=AB
∠ABD=∠ABC
ASA
AC=AD
ABD
已知
已知
ABC
ABD
做一做
例4 已知:如图,∠1=∠2,∠C=∠E,AC=AE.
求证:△ABC≌△ADE
1
2
C
A
B
E
D
例题讲解
∵∠1=∠2
∴∠1+∠BAE=∠2+∠BAE
在△ABC与△ADE中
∴△ABC≌△ADE
证明:
∠BAC=∠DAE
AC=AE
∠C=∠E
( ASA)
(已知)
(已知)
(已知)
(已证)
即∠BAC=∠DAE
例5 如图,点B,F,E,C在同一条直线上,AB∥CD,且AB=CD ,∠A=∠D.求证:AE=DF
F
E
D
C
B
A
例题讲解
∵AB∥CD
∴∠B=∠C
在△ABE和△DCF中
∴△ABE≌△DCF
证明:
∠A=∠D
AB=DC
∠B=∠C
( ASA)
(两直线平行,
内错角相等)
(已证)
(已知)
(已知)
∴AE=DF
(全等三角形的对应角相等)
1.某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( ).
带①去 B.带②去
C. 带③去 D.带①和②去
①
②
③
C
练一练
在△ABD和△ACE中,
∠B=∠C(已知)
AB=AC (已知)
∠A=∠A(公共角)
∴ △ABD≌△ACE (ASA)
∴AE=AD
2. 已知:AB=AC,∠B=∠C,
求证:AE=AD
A
B
D
C
E
证明:
练一练
一展身手
3.如图,AB=AC,∠1=∠2,∠B=∠C,请说明下列结论成立的理由:
(1)△ABE≌△ACD;(2)AD=AE.
A
B
D
C
E
1
2
一展身手
4.如图, △ABC的两条高AD,BE相交于H,且AD=BD,试说明 △BDH ≌△ADC.
A
B
D
C
E
H
小结
1.判定两个三角形全等的条件:
① 能完全重合的两个三角形是全等三角形
② 有三条边对应相等的两个三角形全等(简称SSS)
③ 有两边和它们的夹角对应相等的两个三角形全等(简称SAS)
2.两个三角形全等的关键:
找符合要求的条件
④两个角及其夹边对应相等的两个三角形全等(简称ASA)
边和角分别对应相等,而不是分别相等.
特别注意:
再见
1.5 三角形全等的判定(三)
浙教版《数学》八年级上册
教学目标
1.探索并掌握两个三角形全等的条件:两个角及其夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”);
2.会用ASA判定两个三角形全等;
体会利用转化的数学思想和方法解决问题的过程.
在探索三角形全等条件及其运用的过程中,能够进行有条理的思考并进行简单推理.
知识目标
能力目标
情感目标
知识回顾
1.要判定两个三角形全等我们已经学过几种方法:
① 能完全重合的两个三角形是全等三角形(定义)
② 有三条边对应相等的两个三角形全等(简称SSS)
③ 有两边和它们的夹角对应相等的两个三角形全等(简称SAS)
2.垂直平分线的性质:
线段垂直平分线上的点到线段两端的距离相等.
如图,AB与CD相交于点O,OA=OB,AD=BC
(2)如果将题中条件AD=BC换成∠A=∠B或∠D=∠C, △OAD与△OBC还能全等吗?
(1)判断△OAD 与△ OBC是否全等?如果全等说明理由;如果不全等,请你添加一个条件,使△OAD ≌△ OBC ,并说明理由.
(写出至少两种情形)
A
B
C
O
D
新课引入
小明不小心将一块三角形模具打碎了,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适?
所带的这块玻璃里有几个条件已知?
新课引入
将你画出的三角形和其他同学画的三角形进行比较,它们互相重合吗?
由此,你得到了什么结论?
合作学习
动手做一做:请用量角器和刻度尺画ΔABC,使BC=3cm,∠B=40°, ∠C=60°,
C
B
A
600
400
3cm
B
C
A
600
400
3cm
A
B
C
D
E
F
两个角及其夹边对应相等的两个三角形全等.
(简写成“角边角”或“ASA”)
三角形全等的判定条件3:
∴△ABC ≌△DEF
∠B= ∠E
BC=EF
(ASA)
在△ABC和△DEF中
几何语言
∵
新课讲解
∠C=∠F
在△ABC和△DEF中
∠A=∠D
____=____
∠B=∠E
∴ △ABC≌△DEF(ASA)
AB DE
A
B
C
D
E
F
1.填一填
做一做
在△ABC和△DEF中
=__ _
AC=DF
=__ _
∴ △ABC≌△DEF(ASA)
∠A ∠D
∠C ∠F
做一做
A
B
C
D
E
F
1
2
3
4
D
A
B
C
如图,∠1=∠2,∠3=∠4,说明:AC=AD
解:∵∠ =180 -∠3
∠ =180 -∠4
而∠3=∠4(已知)
∴∠ABD=∠ABC
在△ 和△ 中
( )
(公共边)
( )
∴△ ≌ △ ( )
∴ (全等三角形对应边相等)
ABD
ABC
ABC
∠1=∠2
AB=AB
∠ABD=∠ABC
ASA
AC=AD
ABD
已知
已知
ABC
ABD
做一做
例4 已知:如图,∠1=∠2,∠C=∠E,AC=AE.
求证:△ABC≌△ADE
1
2
C
A
B
E
D
例题讲解
∵∠1=∠2
∴∠1+∠BAE=∠2+∠BAE
在△ABC与△ADE中
∴△ABC≌△ADE
证明:
∠BAC=∠DAE
AC=AE
∠C=∠E
( ASA)
(已知)
(已知)
(已知)
(已证)
即∠BAC=∠DAE
例5 如图,点B,F,E,C在同一条直线上,AB∥CD,且AB=CD ,∠A=∠D.求证:AE=DF
F
E
D
C
B
A
例题讲解
∵AB∥CD
∴∠B=∠C
在△ABE和△DCF中
∴△ABE≌△DCF
证明:
∠A=∠D
AB=DC
∠B=∠C
( ASA)
(两直线平行,
内错角相等)
(已证)
(已知)
(已知)
∴AE=DF
(全等三角形的对应角相等)
1.某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( ).
带①去 B.带②去
C. 带③去 D.带①和②去
①
②
③
C
练一练
在△ABD和△ACE中,
∠B=∠C(已知)
AB=AC (已知)
∠A=∠A(公共角)
∴ △ABD≌△ACE (ASA)
∴AE=AD
2. 已知:AB=AC,∠B=∠C,
求证:AE=AD
A
B
D
C
E
证明:
练一练
一展身手
3.如图,AB=AC,∠1=∠2,∠B=∠C,请说明下列结论成立的理由:
(1)△ABE≌△ACD;(2)AD=AE.
A
B
D
C
E
1
2
一展身手
4.如图, △ABC的两条高AD,BE相交于H,且AD=BD,试说明 △BDH ≌△ADC.
A
B
D
C
E
H
小结
1.判定两个三角形全等的条件:
① 能完全重合的两个三角形是全等三角形
② 有三条边对应相等的两个三角形全等(简称SSS)
③ 有两边和它们的夹角对应相等的两个三角形全等(简称SAS)
2.两个三角形全等的关键:
找符合要求的条件
④两个角及其夹边对应相等的两个三角形全等(简称ASA)
边和角分别对应相等,而不是分别相等.
特别注意:
再见
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
