4.4.1两个三角形相似的判定 课件(共24张PPT)
文档属性
| 名称 | 4.4.1两个三角形相似的判定 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 15:39:37 | ||
图片预览








文档简介
(共24张PPT)
4.4.1两个三角形相似的判定
浙教版 九年级上册
教学目标
教学目标:
1.使学生理解相似三角形的定义,掌握定义中的两个条件.
2.使学生掌握相似三角形判定定理1.
重点:准确找出相似三角形的对应边和对应角.
难点:掌握相似三角形判定定理1及其应用.
新课导入
判定两个三角形全等时,除了可以验证它们所有的角和边分别相等外,还可以使用简便的判定方法(SSS,SAS,ASA,AAS).
类似地,判定两个三角形相似时,是不是也存在简便的判定方法呢?
新知探究
如图,在△ABC中,D,E分别是AB,AC上的点,DE//BC.
△ADE与△ABC相似吗?
分析:△ADE 与△ABC 的三个角分别相等吗?
分别度量△ADE 与△ABC 的边长,它们的边长是否对应成比例?
新知探究
B
C
A
D
E
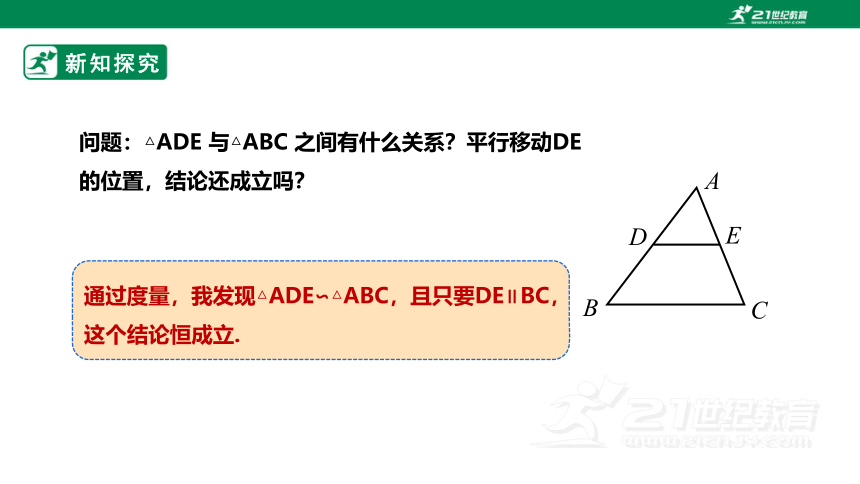
通过度量,我发现△ADE∽△ABC,且只要DE∥BC,这个结论恒成立.
问题:△ADE 与△ABC 之间有什么关系?平行移动DE 的位置,结论还成立吗?
新知探究
B
C
A
D
E
问题:要用相似的定义去证明△ADE∽△ABC ,我们需要证明什么?
而除 DE 外,其他的线段都在△ABC 的边上,要想利用前面得到的结论来证明三角形相似,需要怎样做呢?
由前面的结论可得 ,需要证明的是
可以将 DE 平移到BC 边上去
新知探究
证明:在 △ADE 与 △ABC 中,∠A=∠A.
∵ DE∥BC,
∴ ∠ADE=∠B,∠AED=∠C.
如图,过点 D 作 DF∥AC,交 BC 于点 F.
C
A
B
D
E
F
用相似的定义证明:△ADE∽△ABC.
∵ DE∥BC,DF∥AC,
∴
∵ 四边形DFCE为平行四边形,
∴ DE=FC,
∴△ADE∽△ABC.
∴
新知探究
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
相似三角形的预备定理:
几何语言:如下图所示,∵DE//BC,∴△ADE∽△ABC.
定理中“和其他两边相交”是指和其他两边所在的直线相交.
新知探究
三角形相似的两种常见类型:
“X ” 型
D
E
A
B
C
“A ”型
A
B
C
D
E
新知探究
如果两个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
判定三角形相似的定理:
两角对应相等,两三角形相似.
A1
B1
C1
A
B
C
△ABC∽△A1B1C1.
即:如果
∠A =∠A1,∠B =∠B1 .
新知探究
下面给出证明.
已知:如图,在△ABC与△A'B'C'中,∠A=∠A',∠B=∠B'.
求证:△ABC∽△A'B'C'.
新知探究
证明: 如图,在A'B'上截取A'D=AB,作DE∥B'C',交AC于点E,
则△A'DE∽△A'B'C'(平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似).
又∵∠A=∠A',∠B=∠B'=∠A'DE,
∴△ABC≌△A'DE,
∴△ABC∽△A'B'C'.
例题讲解
例1、在一次数学活动课上,为了测量河宽AB,小聪采用了如下方法:从A处沿与AB垂直的直线方向走45m到达C处,插一根标杆,然后沿同方向继续走15m到达D处,再右转90°走到E处,使B,C,E三点恰好在一条直线上,量得DE=20m,这样就可以求出河宽AB.请你算出结果(要求给出解题过程)
B.
A.
C
D
E
方法一
方法二 方法三
例题讲解
解:∵AB⊥AD,DE⊥AD
∴∠BAC=∠EDC=Rt∠
又∵∠ACB=∠DCE ∴△ABC∽△DEC
∴ 即AB=
∵AC=45,CD=15,DE=20
∴AB=
答:河宽AB是60m.
B.
A.
C
D
E
课堂练习
1.如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_________
A
B
C
D
E
F
G
H
I
△ADG∽△AEH∽△AFI∽△ABC
1:4
课堂练习
2. 如图,已知 AB∥DE,∠AFC =∠E,则图中相似三角形共有( )
A. 1对 B. 2对
C. 3对 D. 4对
C
A
B
D
C
3. 如图,点 D 在 AB上,当∠ =∠ (或∠ =∠ )时,△ACD∽△ABC;
ACD
ACB
B
ADC
课堂练习
4.如图,在 △ABC 和 △A'B'C' 中,若∠A=50°,∠B=75°,∠A' = 50°,当∠C'= 时,△ABC ∽△A'B'C'.
C
A
B
B'
C'
A'
55°
课堂练习
5.在△ABC与△DEF中,∠A=∠D=70°,∠B=60°,∠E=50°, 这两个三角形相似吗?为什么?
解:相似.
根据三角形内角和定理,
可得∠C=50°,即∠C=∠E,
又已知∠A=∠D,
所以△ABC∽△DEF.
课堂练习
6.如图,在四边形ABCD中,AB∥CD,对角线AC与BD相交于点O.找出图中的相似三角形,并说明理由.
A
B
C
D
O
解:∵AB∥CD,
∴∠OAB=∠OCD,∠OBA=∠ODC
∴△ABO∽△CDO.
课堂练习
7.如图,在边长为4的等边三角形ABC中,D、E分别在线段BC,AC上运动,在运动过程中始终保持∠ADE=60°,求证:△ABD∽△DCE.
证明:∵△ABC是等边三角形,
∴∠B=∠C=60°.
∴∠BAD+∠ADB=120°.
∵∠ADE=60°,
∴∠ADB+∠EDC=120°.
∴∠DAB=∠EDC.
∴△ABD∽△DCE.
课堂练习
8.如图,在△ABC 和 △DEF 中,∠A=40°,∠B=80°,∠E=80 °,∠F=60 °.求证:△ABC ∽△DEF.
A
C
B
F
E
D
证明:∵ 在△ ABC中,∠A=40 ° ,∠B=80 ° ,
∴ ∠C=180 °-∠A-∠B=60 °.
∵ 在△DEF中,∠E=80 °,∠F=60 °.
∴ ∠B=∠E,∠C=∠F.
∴ △ABC ∽△DEF.
课堂小结
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
相似三角形的预备定理:
如果两个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
判定三角形相似的定理:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
4.4.1两个三角形相似的判定
浙教版 九年级上册
教学目标
教学目标:
1.使学生理解相似三角形的定义,掌握定义中的两个条件.
2.使学生掌握相似三角形判定定理1.
重点:准确找出相似三角形的对应边和对应角.
难点:掌握相似三角形判定定理1及其应用.
新课导入
判定两个三角形全等时,除了可以验证它们所有的角和边分别相等外,还可以使用简便的判定方法(SSS,SAS,ASA,AAS).
类似地,判定两个三角形相似时,是不是也存在简便的判定方法呢?
新知探究
如图,在△ABC中,D,E分别是AB,AC上的点,DE//BC.
△ADE与△ABC相似吗?
分析:△ADE 与△ABC 的三个角分别相等吗?
分别度量△ADE 与△ABC 的边长,它们的边长是否对应成比例?
新知探究
B
C
A
D
E
通过度量,我发现△ADE∽△ABC,且只要DE∥BC,这个结论恒成立.
问题:△ADE 与△ABC 之间有什么关系?平行移动DE 的位置,结论还成立吗?
新知探究
B
C
A
D
E
问题:要用相似的定义去证明△ADE∽△ABC ,我们需要证明什么?
而除 DE 外,其他的线段都在△ABC 的边上,要想利用前面得到的结论来证明三角形相似,需要怎样做呢?
由前面的结论可得 ,需要证明的是
可以将 DE 平移到BC 边上去
新知探究
证明:在 △ADE 与 △ABC 中,∠A=∠A.
∵ DE∥BC,
∴ ∠ADE=∠B,∠AED=∠C.
如图,过点 D 作 DF∥AC,交 BC 于点 F.
C
A
B
D
E
F
用相似的定义证明:△ADE∽△ABC.
∵ DE∥BC,DF∥AC,
∴
∵ 四边形DFCE为平行四边形,
∴ DE=FC,
∴△ADE∽△ABC.
∴
新知探究
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
相似三角形的预备定理:
几何语言:如下图所示,∵DE//BC,∴△ADE∽△ABC.
定理中“和其他两边相交”是指和其他两边所在的直线相交.
新知探究
三角形相似的两种常见类型:
“X ” 型
D
E
A
B
C
“A ”型
A
B
C
D
E
新知探究
如果两个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
判定三角形相似的定理:
两角对应相等,两三角形相似.
A1
B1
C1
A
B
C
△ABC∽△A1B1C1.
即:如果
∠A =∠A1,∠B =∠B1 .
新知探究
下面给出证明.
已知:如图,在△ABC与△A'B'C'中,∠A=∠A',∠B=∠B'.
求证:△ABC∽△A'B'C'.
新知探究
证明: 如图,在A'B'上截取A'D=AB,作DE∥B'C',交AC于点E,
则△A'DE∽△A'B'C'(平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似).
又∵∠A=∠A',∠B=∠B'=∠A'DE,
∴△ABC≌△A'DE,
∴△ABC∽△A'B'C'.
例题讲解
例1、在一次数学活动课上,为了测量河宽AB,小聪采用了如下方法:从A处沿与AB垂直的直线方向走45m到达C处,插一根标杆,然后沿同方向继续走15m到达D处,再右转90°走到E处,使B,C,E三点恰好在一条直线上,量得DE=20m,这样就可以求出河宽AB.请你算出结果(要求给出解题过程)
B.
A.
C
D
E
方法一
方法二 方法三
例题讲解
解:∵AB⊥AD,DE⊥AD
∴∠BAC=∠EDC=Rt∠
又∵∠ACB=∠DCE ∴△ABC∽△DEC
∴ 即AB=
∵AC=45,CD=15,DE=20
∴AB=
答:河宽AB是60m.
B.
A.
C
D
E
课堂练习
1.如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_________
A
B
C
D
E
F
G
H
I
△ADG∽△AEH∽△AFI∽△ABC
1:4
课堂练习
2. 如图,已知 AB∥DE,∠AFC =∠E,则图中相似三角形共有( )
A. 1对 B. 2对
C. 3对 D. 4对
C
A
B
D
C
3. 如图,点 D 在 AB上,当∠ =∠ (或∠ =∠ )时,△ACD∽△ABC;
ACD
ACB
B
ADC
课堂练习
4.如图,在 △ABC 和 △A'B'C' 中,若∠A=50°,∠B=75°,∠A' = 50°,当∠C'= 时,△ABC ∽△A'B'C'.
C
A
B
B'
C'
A'
55°
课堂练习
5.在△ABC与△DEF中,∠A=∠D=70°,∠B=60°,∠E=50°, 这两个三角形相似吗?为什么?
解:相似.
根据三角形内角和定理,
可得∠C=50°,即∠C=∠E,
又已知∠A=∠D,
所以△ABC∽△DEF.
课堂练习
6.如图,在四边形ABCD中,AB∥CD,对角线AC与BD相交于点O.找出图中的相似三角形,并说明理由.
A
B
C
D
O
解:∵AB∥CD,
∴∠OAB=∠OCD,∠OBA=∠ODC
∴△ABO∽△CDO.
课堂练习
7.如图,在边长为4的等边三角形ABC中,D、E分别在线段BC,AC上运动,在运动过程中始终保持∠ADE=60°,求证:△ABD∽△DCE.
证明:∵△ABC是等边三角形,
∴∠B=∠C=60°.
∴∠BAD+∠ADB=120°.
∵∠ADE=60°,
∴∠ADB+∠EDC=120°.
∴∠DAB=∠EDC.
∴△ABD∽△DCE.
课堂练习
8.如图,在△ABC 和 △DEF 中,∠A=40°,∠B=80°,∠E=80 °,∠F=60 °.求证:△ABC ∽△DEF.
A
C
B
F
E
D
证明:∵ 在△ ABC中,∠A=40 ° ,∠B=80 ° ,
∴ ∠C=180 °-∠A-∠B=60 °.
∵ 在△DEF中,∠E=80 °,∠F=60 °.
∴ ∠B=∠E,∠C=∠F.
∴ △ABC ∽△DEF.
课堂小结
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
相似三角形的预备定理:
如果两个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
判定三角形相似的定理:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
