4.2平面直角坐标系(1) 课件(22张PPT)
文档属性
| 名称 | 4.2平面直角坐标系(1) 课件(22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 17:02:36 | ||
图片预览




文档简介
(共22张PPT)
浙教版 八年级上册
4.2 平面直角坐标系 (1)
借助三角板,垂直处理,锁定坐标,确定位置
1.如图,说出数轴上各点所表示的数:
数轴上的点A表示数__.
B
0
1
2
3
-1
-2
-3
-4
A
同理可知,点B在数轴上的坐标是___;记为 B(-1)
-1表示点___的位置。
3
-1
B
我们说数3是点A在数轴上的坐标,记为 A(3)。
A
温故知新:
反过来数3就是点__的位置。
.
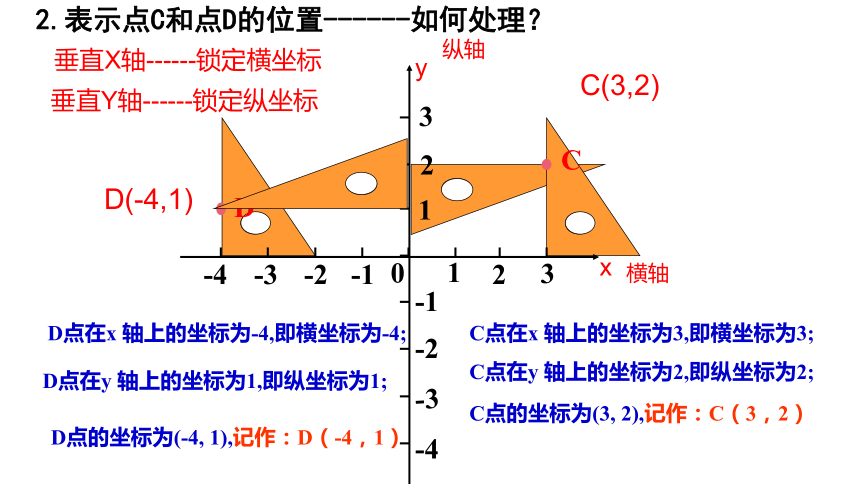
2.表示点C和点D的位置------如何处理?
C
0
1
2
3
-1
-2
-3
-4
D
1
2
3
-1
-2
-3
-4
x
y
C(3,2)
D(-4,1)
垂直X轴------锁定横坐标
C点在x 轴上的坐标为3,即横坐标为3;
C点在y 轴上的坐标为2,即纵坐标为2;
C点的坐标为(3, 2),记作:C(3,2)
D点在x 轴上的坐标为-4,即横坐标为-4;
D点在y 轴上的坐标为1,即纵坐标为1;
D点的坐标为(-4, 1),记作:D(-4,1)
横轴
纵轴
垂直Y轴------锁定纵坐标
用两条互相垂直的数轴来表示平面内物体位置,
在数学上称为平面直角坐标系.
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系. 水平的数轴叫做轴(或横轴),习惯上取向右为正方向;铅直的数轴叫做轴(或纵轴),取向上为正方向;两坐标轴的交点为原点,用O表示.如图所示
建立了平面直角坐标系的平面称为坐标平面,
平面直角坐标系也简称为直角坐标系.
x轴-----横轴------水平线
y轴-----纵轴------铅直线
0
1
2
3
4
5
-4
-3
-2
-1
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
第一象限
第二象限
第三象限
第四象限
0
1
2
3
4
5
-4
-3
-2
-1
1
2
3
4
5
-4
-3
-2
-1
x
y
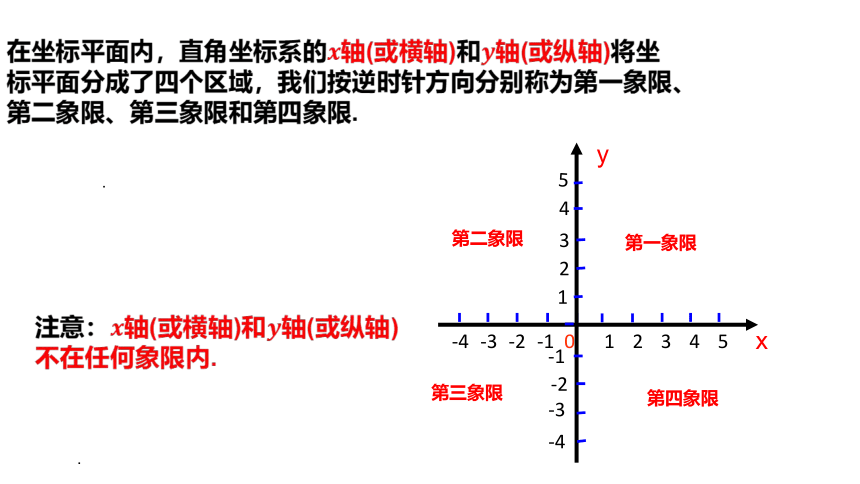
在坐标平面内,直角坐标系的轴(或横轴)和轴(或纵轴)将坐标平面分成了四个区域,我们按逆时针方向分别称为第一象限、第二象限、第三象限和第四象限.
.
注意:轴(或横轴)和轴(或纵轴)不在任何象限内.
.
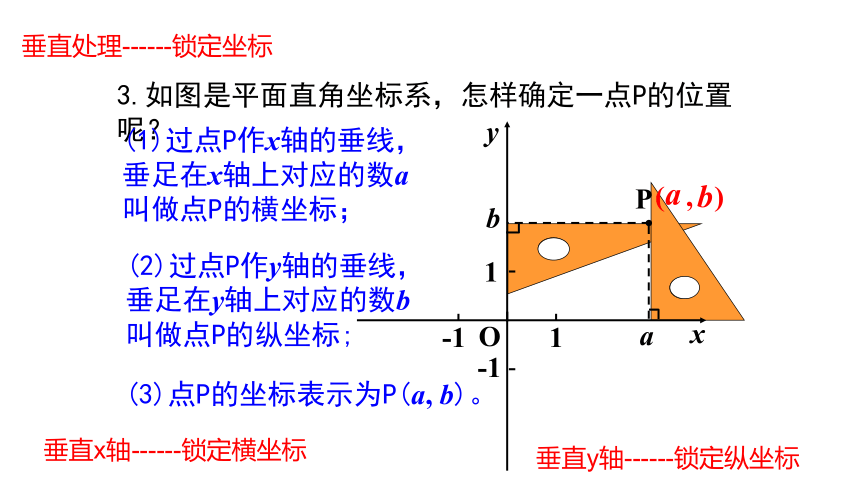
3.如图是平面直角坐标系,怎样确定一点P的位置呢?
1
-1
y
-1
O
1
x
P
a
b
( , )
(1)过点P作x轴的垂线,
垂足在x轴上对应的数a
叫做点P的横坐标;
(2)过点P作y轴的垂线,
垂足在y轴上对应的数b
叫做点P的纵坐标;
(3)点P的坐标表示为P(a, b)。
a
b
垂直处理------锁定坐标
垂直x轴------锁定横坐标
垂直y轴------锁定纵坐标
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
0
A
(4,3)
x
y
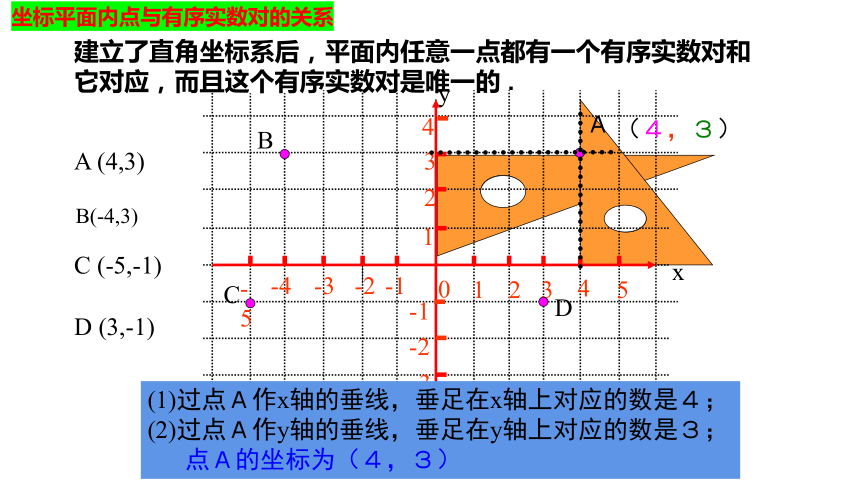
A (4,3)
(1)过点A作x轴的垂线,垂足在x轴上对应的数是4;
(2)过点A作y轴的垂线,垂足在y轴上对应的数是3;
点A的坐标为(4,3)
B
C
D
坐标平面内点与有序实数对的关系
建立了直角坐标系后,平面内任意一点都有一个有序实数对和它对应,而且这个有序实数对是唯一的 .
B(-4,3)
C (-5,-1)
D (3,-1)
·
A
( 4,5 )
在平面直角坐标系中如何由坐标描点?
A(4,5)
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
y
x
垂直处理------锁定坐标
三角板的价值--------垂直处理
由坐标找点的方法:
(1)先找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
A
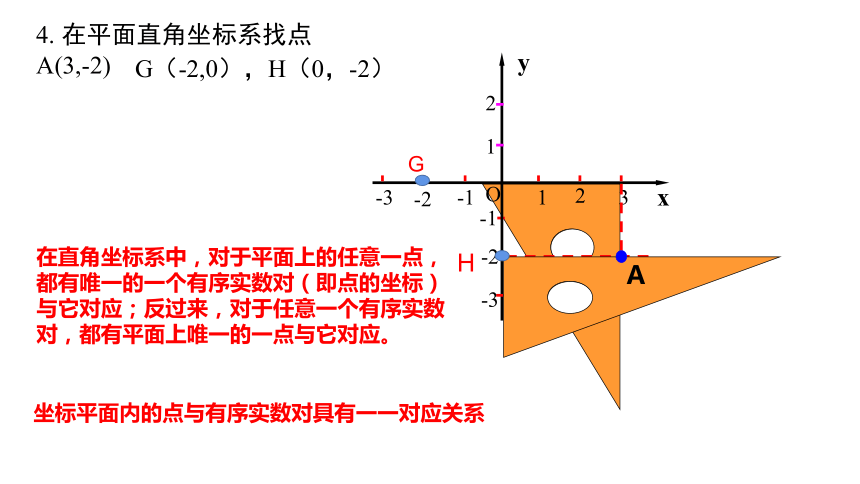
4. 在平面直角坐标系找点A(3,-2)
G(-2,0),H(0,-2)
G
H
在直角坐标系中,对于平面上的任意一点,都有唯一的一个有序实数对(即点的坐标)与它对应;反过来,对于任意一个有序实数对,都有平面上唯一的一点与它对应。
坐标平面内的点与有序实数对具有一一对应关系
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
X
F(0,-6)
5.X 轴上,点的纵坐标为_
y 轴上,点的横坐标为
0
0
注 意:坐标轴上的点不属于任何象限。
数轴上的点与实数一一对应.
平面内的点与有序实数对也是一一对应的.
A
B
C
F
(5,0)
(0,4)
(-6,0)
垂直x轴------锁定横坐标
垂直y轴------锁定纵坐标
一、坐标轴上的点的特征 .
1
1
2
3
4
-1
-2
-3
-4
2
3
4
-1
-2
-3
-4
O
说出点A、B、C、D的坐标
B
C
D
A
P点在轴上 P() ;
原点坐标(0 , 0)
P点在轴上 P() ;
.
坐标平面内点的坐标特征
总结:
A(2.5,0)
C(0,2.5)
B(-4,0)
D(0,-3)
设P() .是坐标平面内任意一点
.
坐标平面内点的坐标特征
二、象限内的点的特征 .
设P() .是坐标平面内任意一点
1
1
2
3
4
-1
-2
-3
-4
2
3
4
-1
-2
-3
-4
A
B
C
D
根据A、B、C、D的坐标,总结各象限内点的坐标特征.
P点在第一象限 ;
P点在第二象限 ;
P点在第三象限 ;
P点在第四象限 .
1
2
3
-1
-2
-3
-4
y
1
2
3
-1
-2
-3
x
0
-4
第四象限
第三象限
第二象限
第一象限
(+, +)
(-, -)
(-, +)
(+, -)
x轴上的点:(a,0)
y轴上的点:(0,b)
点P(a,b)位置 特征:
注 意:坐标轴上的点不属于任何象限。
任何一个在 y轴上的
点的横坐标都为0。
任何一个在 x轴上的
点的纵坐标都为0。
6.坐标平面内点到坐标轴和原点的距离
一、P() 到轴的距离 .
设P() .是坐标平面内任意一点
1
1
2
3
4
-1
-2
-3
-4
2
3
4
-1
-2
-3
-4
P
P
P点到轴的距离=
.
P点到轴的距离= ;
.
P点到原点的距离= ;
.
A
B
C
E
F
D
1:写出下图中的多边形ABCDEF各个顶点的坐标及所在坐标系的位置
1
2
3
4
-1
-2
1
2
3
-1
-2
-3
【答案】
A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
y
O
x
当堂检测:
夯实基础,稳扎稳打
A(3,6)
B(0,-8)
C(-7,-5)
D(-6,0)
E(-3.6,5)
F(5,-6)
G(0,0)
第一象限
第三象限
第二象限
第四象限
y 轴上
x 轴上
原点
2.下列各点分别在坐标平面的什么位置上?
选择题
3.点P位于y轴左方,距y轴3个单位长,则点P的坐标可能是( ).
A、(3,-4) B、(-3,4)
C、(4,-3) D、(-4,3)
4.直角坐标系中,点P(x,y)在第二象限,且 P 到x 轴、y轴距离分别为3,7,则点P坐标为( ).
A、(-3,-7) B、(-7,3)
C、(3,7) D、(7,3)
B
B
6、横坐标是正数,纵坐标的绝对值是正数的点在( )
A、第一、三象限 B、第二、四象限 C、第二、三象限 D、第一、四象限
7、若点P(a,b)在第二象限,则点Q(b,a)在( )
A、第一象限;B、第二象限;C、第三象限;D、第四象限
D
D
连续递推,豁然开朗
5.实数 x,y满足 x2+ y2= 0,则点 P( x,y)在( )
A、原点 B、x轴正半轴 C、第一象限 D、任意位置
A
8、若点P(X, Y)的坐标满足X Y = 0,则点P在 上。
横轴或纵轴
9.已知a二
10.若点P(x,y)在第四象限,|x|=5,|y|=4,则P点的坐标为 .
(5,-4)
∴P(-6 , 0)
∴P(0 , 12)
11.已知点P(,2),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点P到轴、轴的距离相等.
.
解:(1)∵点P在轴上,
.
∴2=0,∴=-4
.
(2)∵点P在轴上,
.
∴=0,∴=2
.
(3)∵点P到轴、轴的距离相等,
.
∴=2 或+2
.
∴,∴=-2
.
∴P(-12 , -12)或P(-4 , 4)
.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版 八年级上册
4.2 平面直角坐标系 (1)
借助三角板,垂直处理,锁定坐标,确定位置
1.如图,说出数轴上各点所表示的数:
数轴上的点A表示数__.
B
0
1
2
3
-1
-2
-3
-4
A
同理可知,点B在数轴上的坐标是___;记为 B(-1)
-1表示点___的位置。
3
-1
B
我们说数3是点A在数轴上的坐标,记为 A(3)。
A
温故知新:
反过来数3就是点__的位置。
.
2.表示点C和点D的位置------如何处理?
C
0
1
2
3
-1
-2
-3
-4
D
1
2
3
-1
-2
-3
-4
x
y
C(3,2)
D(-4,1)
垂直X轴------锁定横坐标
C点在x 轴上的坐标为3,即横坐标为3;
C点在y 轴上的坐标为2,即纵坐标为2;
C点的坐标为(3, 2),记作:C(3,2)
D点在x 轴上的坐标为-4,即横坐标为-4;
D点在y 轴上的坐标为1,即纵坐标为1;
D点的坐标为(-4, 1),记作:D(-4,1)
横轴
纵轴
垂直Y轴------锁定纵坐标
用两条互相垂直的数轴来表示平面内物体位置,
在数学上称为平面直角坐标系.
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系. 水平的数轴叫做轴(或横轴),习惯上取向右为正方向;铅直的数轴叫做轴(或纵轴),取向上为正方向;两坐标轴的交点为原点,用O表示.如图所示
建立了平面直角坐标系的平面称为坐标平面,
平面直角坐标系也简称为直角坐标系.
x轴-----横轴------水平线
y轴-----纵轴------铅直线
0
1
2
3
4
5
-4
-3
-2
-1
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
第一象限
第二象限
第三象限
第四象限
0
1
2
3
4
5
-4
-3
-2
-1
1
2
3
4
5
-4
-3
-2
-1
x
y
在坐标平面内,直角坐标系的轴(或横轴)和轴(或纵轴)将坐标平面分成了四个区域,我们按逆时针方向分别称为第一象限、第二象限、第三象限和第四象限.
.
注意:轴(或横轴)和轴(或纵轴)不在任何象限内.
.
3.如图是平面直角坐标系,怎样确定一点P的位置呢?
1
-1
y
-1
O
1
x
P
a
b
( , )
(1)过点P作x轴的垂线,
垂足在x轴上对应的数a
叫做点P的横坐标;
(2)过点P作y轴的垂线,
垂足在y轴上对应的数b
叫做点P的纵坐标;
(3)点P的坐标表示为P(a, b)。
a
b
垂直处理------锁定坐标
垂直x轴------锁定横坐标
垂直y轴------锁定纵坐标
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
0
A
(4,3)
x
y
A (4,3)
(1)过点A作x轴的垂线,垂足在x轴上对应的数是4;
(2)过点A作y轴的垂线,垂足在y轴上对应的数是3;
点A的坐标为(4,3)
B
C
D
坐标平面内点与有序实数对的关系
建立了直角坐标系后,平面内任意一点都有一个有序实数对和它对应,而且这个有序实数对是唯一的 .
B(-4,3)
C (-5,-1)
D (3,-1)
·
A
( 4,5 )
在平面直角坐标系中如何由坐标描点?
A(4,5)
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
y
x
垂直处理------锁定坐标
三角板的价值--------垂直处理
由坐标找点的方法:
(1)先找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
A
4. 在平面直角坐标系找点A(3,-2)
G(-2,0),H(0,-2)
G
H
在直角坐标系中,对于平面上的任意一点,都有唯一的一个有序实数对(即点的坐标)与它对应;反过来,对于任意一个有序实数对,都有平面上唯一的一点与它对应。
坐标平面内的点与有序实数对具有一一对应关系
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
X
F(0,-6)
5.X 轴上,点的纵坐标为_
y 轴上,点的横坐标为
0
0
注 意:坐标轴上的点不属于任何象限。
数轴上的点与实数一一对应.
平面内的点与有序实数对也是一一对应的.
A
B
C
F
(5,0)
(0,4)
(-6,0)
垂直x轴------锁定横坐标
垂直y轴------锁定纵坐标
一、坐标轴上的点的特征 .
1
1
2
3
4
-1
-2
-3
-4
2
3
4
-1
-2
-3
-4
O
说出点A、B、C、D的坐标
B
C
D
A
P点在轴上 P() ;
原点坐标(0 , 0)
P点在轴上 P() ;
.
坐标平面内点的坐标特征
总结:
A(2.5,0)
C(0,2.5)
B(-4,0)
D(0,-3)
设P() .是坐标平面内任意一点
.
坐标平面内点的坐标特征
二、象限内的点的特征 .
设P() .是坐标平面内任意一点
1
1
2
3
4
-1
-2
-3
-4
2
3
4
-1
-2
-3
-4
A
B
C
D
根据A、B、C、D的坐标,总结各象限内点的坐标特征.
P点在第一象限 ;
P点在第二象限 ;
P点在第三象限 ;
P点在第四象限 .
1
2
3
-1
-2
-3
-4
y
1
2
3
-1
-2
-3
x
0
-4
第四象限
第三象限
第二象限
第一象限
(+, +)
(-, -)
(-, +)
(+, -)
x轴上的点:(a,0)
y轴上的点:(0,b)
点P(a,b)位置 特征:
注 意:坐标轴上的点不属于任何象限。
任何一个在 y轴上的
点的横坐标都为0。
任何一个在 x轴上的
点的纵坐标都为0。
6.坐标平面内点到坐标轴和原点的距离
一、P() 到轴的距离 .
设P() .是坐标平面内任意一点
1
1
2
3
4
-1
-2
-3
-4
2
3
4
-1
-2
-3
-4
P
P
P点到轴的距离=
.
P点到轴的距离= ;
.
P点到原点的距离= ;
.
A
B
C
E
F
D
1:写出下图中的多边形ABCDEF各个顶点的坐标及所在坐标系的位置
1
2
3
4
-1
-2
1
2
3
-1
-2
-3
【答案】
A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
y
O
x
当堂检测:
夯实基础,稳扎稳打
A(3,6)
B(0,-8)
C(-7,-5)
D(-6,0)
E(-3.6,5)
F(5,-6)
G(0,0)
第一象限
第三象限
第二象限
第四象限
y 轴上
x 轴上
原点
2.下列各点分别在坐标平面的什么位置上?
选择题
3.点P位于y轴左方,距y轴3个单位长,则点P的坐标可能是( ).
A、(3,-4) B、(-3,4)
C、(4,-3) D、(-4,3)
4.直角坐标系中,点P(x,y)在第二象限,且 P 到x 轴、y轴距离分别为3,7,则点P坐标为( ).
A、(-3,-7) B、(-7,3)
C、(3,7) D、(7,3)
B
B
6、横坐标是正数,纵坐标的绝对值是正数的点在( )
A、第一、三象限 B、第二、四象限 C、第二、三象限 D、第一、四象限
7、若点P(a,b)在第二象限,则点Q(b,a)在( )
A、第一象限;B、第二象限;C、第三象限;D、第四象限
D
D
连续递推,豁然开朗
5.实数 x,y满足 x2+ y2= 0,则点 P( x,y)在( )
A、原点 B、x轴正半轴 C、第一象限 D、任意位置
A
8、若点P(X, Y)的坐标满足X Y = 0,则点P在 上。
横轴或纵轴
9.已知a
10.若点P(x,y)在第四象限,|x|=5,|y|=4,则P点的坐标为 .
(5,-4)
∴P(-6 , 0)
∴P(0 , 12)
11.已知点P(,2),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点P到轴、轴的距离相等.
.
解:(1)∵点P在轴上,
.
∴2=0,∴=-4
.
(2)∵点P在轴上,
.
∴=0,∴=2
.
(3)∵点P到轴、轴的距离相等,
.
∴=2 或+2
.
∴,∴=-2
.
∴P(-12 , -12)或P(-4 , 4)
.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
