4.2平面直角坐标系(2) 课件(24张PPT)
文档属性
| 名称 | 4.2平面直角坐标系(2) 课件(24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 17:09:47 | ||
图片预览





文档简介
(共24张PPT)
浙教版 八年级上册
4.2 平面直角坐标系 (2)
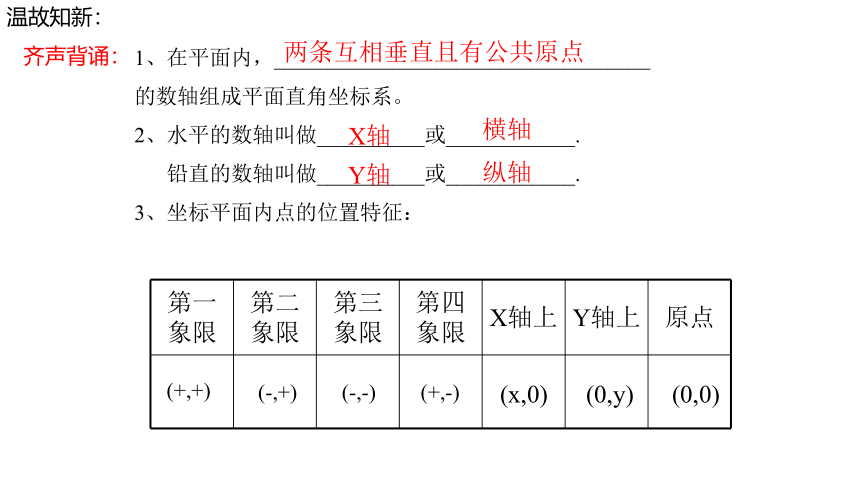
1、在平面内,___________________________________
的数轴组成平面直角坐标系。
2、水平的数轴叫做__________或____________.
铅直的数轴叫做__________或____________.
3、坐标平面内点的位置特征:
第一象限 第二象限 第三象限 第四象限 X轴上 Y轴上 原点
(+,+)
(-,+)
(-,-)
(+,-)
(x,0)
(0,y)
(0,0)
两条互相垂直且有公共原点
X轴
横轴
Y轴
纵轴
温故知新:
齐声背诵:
1
2
3
-1
-2
-3
-4
y
1
2
3
-1
-2
-3
x
0
-4
第四象限
第三象限
第二象限
第一象限
(+, +)
(-, -)
(-, +)
(+, -)
x轴上的点:(a,0)
y轴上的点:(0,b)
点P(a,b)位置 特征:
注 意:坐标轴上的点不属于任何象限。
任何一个在 y轴上的
点的横坐标都为0。
任何一个在 x轴上的
点的纵坐标都为0。
A
B
D
C
1、对于正方形ABCD,建立如图所示的直角坐标系,写出A、B、C、D各顶点坐标
解:A、B、C、D各顶点坐标为
A(-4,-4),B(4,-4),
C(4,4), D(-4,4)。
x
y
o
边长为一个单位长度的正方形网格
在建立直角坐标系表示给定的点或图形的位置时,一般应选择适当的点作为原点,适当的直线作为坐标轴,适当的距离为单位长度,这样往往有助于表示和解决有关问题
A
B
D
C
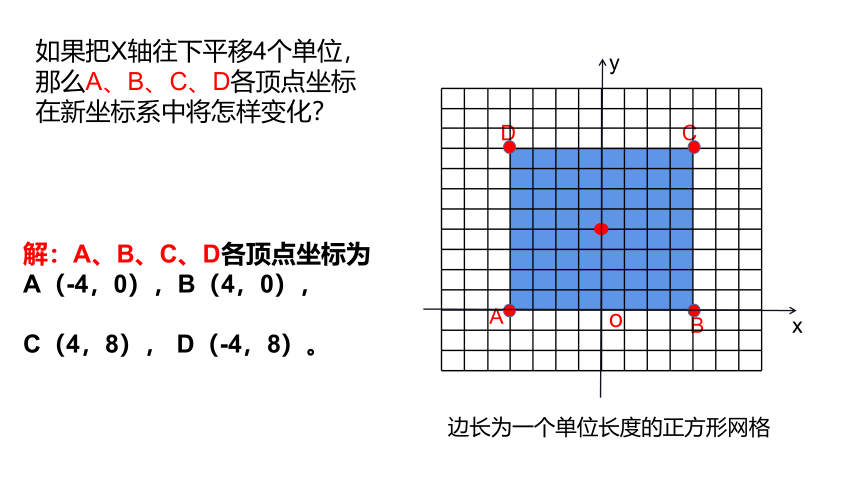
解:A、B、C、D各顶点坐标为
A(-4,0),B(4,0),
C(4,8), D(-4,8)。
x
y
o
边长为一个单位长度的正方形网格
如果把X轴往下平移4个单位,那么A、B、C、D各顶点坐标在新坐标系中将怎样变化?
2、一个四边形的形状和尺寸如图所示,建立适当的直角坐标系,在坐标系中作出四边形,并标出各顶点的坐标:
B
单位:mm
A
D
150
100
200
200
50
C
E
X(cm)
Y(cm)
1
3
2
4
C(2.5,1.5)
解:建立直角坐标系如右图,选择比例为1:10,取点E为直角坐标系的原点,使四边形的线段AB在X轴上,则可得A、B、C、D各点的坐标分别为
A(-1,0)
B(2,0)
0
1
3
2
-1
D(0,3.5)
如图中的四边形ABCD就是所求作的图形
(-1,0),(2,0)
(2.5,1.5),(0,3.5)
X
150
100
200
200
50
C
E
A
D
B
若以A为坐标原点, 建立适当的坐标系,你能写出ABCD各点的坐标吗
y
x
A
解:建立直角坐标系如右图,选择比例为1:10,取点A为直角坐标系的原点,线段AB在X轴上,则可得A、B、C、D各点的坐标分别为:
3
2
1
3
4
2
1
B(3,0)
4
C(3.5,1.5)
(0,0)
D(1,3.5)
如上图中的四边形ABCD就是所求作的图形
用线段依次连结各点
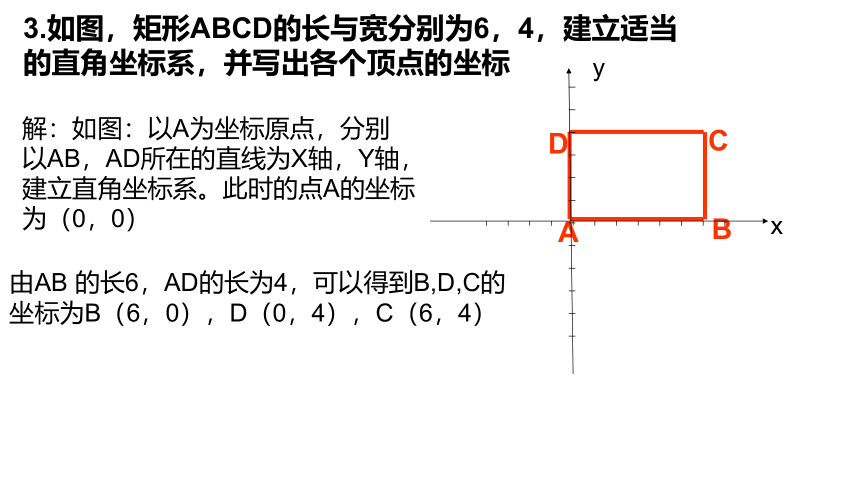
3.如图,矩形ABCD的长与宽分别为6,4,建立适当的直角坐标系,并写出各个顶点的坐标
A
B
C
D
由AB 的长6,AD的长为4,可以得到B,D,C的坐标为B(6,0),D(0,4),C(6,4)
x
y
解:如图:以A为坐标原点,分别
以AB,AD所在的直线为X轴,Y轴,
建立直角坐标系。此时的点A的坐标
为(0,0)
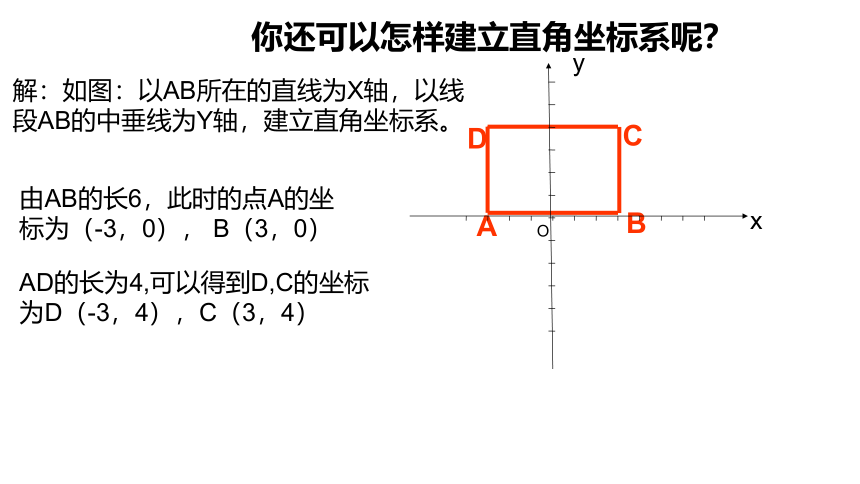
你还可以怎样建立直角坐标系呢?
A
B
C
D
解:如图:以AB所在的直线为X轴,以线段AB的中垂线为Y轴,建立直角坐标系。
由AB的长6,此时的点A的坐
标为(-3,0), B(3,0)
AD的长为4,可以得到D,C的坐标
为D(-3,4),C(3,4)
x
y
O
解:以线段AD的中垂线为x轴,线段AB的中垂线为y轴,建立平面直角坐标系
由于线段AB长为6,线段AD长为4,
则各点的坐标分别为
A(-3,-2)、B(3,-2)、C(3,2)、D(-3,2)
x
y
O
A
B
C
D
要确定某点的位置在于, 建立适当的直角坐标系。
1.选择适当的点作为原点;(充分利用特殊点)
2.适当的直线作为坐标轴(充分利用特殊边)
3.选择适当的距离为单位长度。
(一般按比例选择)
归 纳
1.若以点B为原点建立平面直角坐标系,点A的坐标为( 3 , 4 ),若以点A为原点建立平面直角坐标系,则点 B 的坐标可能是( )
A .(-3 ,-4) B .(-3 ,4) C .(3 ,-4) D .(3, 4)
1
1
2
3
4
-1
-2
-3
-4
2
3
4
-1
-2
-3
-4
0
A
B
A
当堂检测:
夯实基础,稳扎稳打
2.如图所示,在象棋盘上建立平面直角坐标系,若“帅”位于点(-1,-2),
“马”位于点(2 ,-2),则“兵”位于点( )
A .(- 1 , 1) B .(- 2 ,- 1)
C .(- 3 , 1) D .( 1 ,- 2)
C
x
y
o
A
B
C
A
B
C
x
y
o
D
┗
2
2
┒
3.等边 △ABC的边长为 2,建立适当的直角坐标系,并求等边 △ABC各个顶点的坐标
法1:BD=1,AD=
.
A(1,)
B(0,0)
C(2,0)
法2:C0=1,A0=
A(0,)
B(-1,0)
C(1,0)
A
B
C
x
y
o
x
y
o
A
B
C
等边 △ABC的边长为 2,建立适当的直角坐标系,并求等边 △ABC各个顶点的坐标
D
┗
2
2
┒
D
法3:CD=1,AD=
.
A(-1,)
B(-2,0)
C(0,0)
法4:CD=1,AD=
.
B(-1,)
A(0,0)
C(1,)
A
B
C
4.腰长为2的等腰Rt△ABC,建立适当的直角坐标系,并写出各顶点的坐标
x
y
O
A
B
C
x
y
O
D
┗
法1:BD=AD=CD=
.
A(,)
B(0,0)
C(2,0)
┛
法2:B0=AD=CD=
.
A(0,)
B(-,0)
C(,0)
A
B
C
A
B
C
x
y
O
x
y
O
腰长为2的等腰Rt△ABC,建立适当的直角坐标系,并写出各顶点的坐标
D
┗
法3:BD=AD=CD=
.
A(,)
C(0,0)
B(-2,0)
法3:BD=AD=CD=
.
B(,)
A(0,0)
C()
┒
D
A
B
C
A
B
C
5.腰长为2、顶角为1200的等腰△ABC,建立适当的直角坐标系,并写出各顶点的坐标
1200
2
2
1200
x
y
O
x
y
O
D
┛
┛
法1:BD=CD=
.AD=1
A(,1)
B(0,0)
C(2,0)
法2:BO=CO=
.AO=1
C(,0)
A(0,1)
B(,0)
A
B
C
A
B
C
2
2
腰长为2、顶角为1200的等腰△ABC,建立适当的直角坐标系,并写出各顶点的坐标
1200
1200
x
y
O
x
y
O
D
┛
法3:BD=CD=
.AD=1
A(,1)
B(,0)
C(0,0)
法4:BD=CD=
.AD=1
┛
D
B(,-1)
C(,1)
A(0,0)
x
y
O
6.Rt△ABC,AB=6,BC=8,在直角坐标系中的位置如图,写出各顶点的坐标
A
B
┛
c
OA=
.
A(10 , 0)
C(0 , 0)
┛
D
6×8=10×BD
BD=4.8
OD=
.
=
.
=
.
=
.
=6.4
B(6.4 , 4.8)
连续递推,豁然开朗
A
B
C
D
∵∠AOB=90°,∴∠AOC+∠BOD=90°.
∵∠AOC+∠OAC=90°,
∴∠OAC=∠BOD.
在△AOC与△BOD中
∴△AOC≌△OBD(AAS).
∴AC=OD, OC=BD
7.如图,△AOB在直角坐标系中,∠AOB=90°,OA=OB,若A(-2 , 3),
点B的坐标和△ABC的面积.
解:分别过A、B作AC⊥轴于C,BD⊥轴于D,
.
.
∵A(-2 , 3)
∴AC=OD=3, OC=BD=2
∴B(3 , 2)
在Rt△AOC中,OA2=OC2+AC2=13,
∴AC=.
.
∴AC=BC= , S△AOB=
.
.
开心图形(K型图)藏其中
8.如图是传说中的一张藏宝岛图,藏宝人生前通过建立直角坐标系(以南北方向为纵轴,东西方向为横轴)画出这幅藏宝图,现在我们只知道图上两块大石头的坐标为A(1,2),B(8,9),而藏宝地的坐标为(5,7),试设法在地图上找到宝藏,并表示出来。
解:根据A、B两点的坐标,可确定原来的坐标系如图
x
y
0
2
4
8
10
6
10
8
6
2
4
A(1,2)
B(8,9)
C(5,7)
图中的点C即藏宝地.
A(1,2)
B(8,9)
D
水平线AD与铅直线BD-----直角
等腰Rt△ABD-----单位长度1
A(1,2)-------坐标原点
藏宝图--------等腰直角三角形藏其中
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版 八年级上册
4.2 平面直角坐标系 (2)
1、在平面内,___________________________________
的数轴组成平面直角坐标系。
2、水平的数轴叫做__________或____________.
铅直的数轴叫做__________或____________.
3、坐标平面内点的位置特征:
第一象限 第二象限 第三象限 第四象限 X轴上 Y轴上 原点
(+,+)
(-,+)
(-,-)
(+,-)
(x,0)
(0,y)
(0,0)
两条互相垂直且有公共原点
X轴
横轴
Y轴
纵轴
温故知新:
齐声背诵:
1
2
3
-1
-2
-3
-4
y
1
2
3
-1
-2
-3
x
0
-4
第四象限
第三象限
第二象限
第一象限
(+, +)
(-, -)
(-, +)
(+, -)
x轴上的点:(a,0)
y轴上的点:(0,b)
点P(a,b)位置 特征:
注 意:坐标轴上的点不属于任何象限。
任何一个在 y轴上的
点的横坐标都为0。
任何一个在 x轴上的
点的纵坐标都为0。
A
B
D
C
1、对于正方形ABCD,建立如图所示的直角坐标系,写出A、B、C、D各顶点坐标
解:A、B、C、D各顶点坐标为
A(-4,-4),B(4,-4),
C(4,4), D(-4,4)。
x
y
o
边长为一个单位长度的正方形网格
在建立直角坐标系表示给定的点或图形的位置时,一般应选择适当的点作为原点,适当的直线作为坐标轴,适当的距离为单位长度,这样往往有助于表示和解决有关问题
A
B
D
C
解:A、B、C、D各顶点坐标为
A(-4,0),B(4,0),
C(4,8), D(-4,8)。
x
y
o
边长为一个单位长度的正方形网格
如果把X轴往下平移4个单位,那么A、B、C、D各顶点坐标在新坐标系中将怎样变化?
2、一个四边形的形状和尺寸如图所示,建立适当的直角坐标系,在坐标系中作出四边形,并标出各顶点的坐标:
B
单位:mm
A
D
150
100
200
200
50
C
E
X(cm)
Y(cm)
1
3
2
4
C(2.5,1.5)
解:建立直角坐标系如右图,选择比例为1:10,取点E为直角坐标系的原点,使四边形的线段AB在X轴上,则可得A、B、C、D各点的坐标分别为
A(-1,0)
B(2,0)
0
1
3
2
-1
D(0,3.5)
如图中的四边形ABCD就是所求作的图形
(-1,0),(2,0)
(2.5,1.5),(0,3.5)
X
150
100
200
200
50
C
E
A
D
B
若以A为坐标原点, 建立适当的坐标系,你能写出ABCD各点的坐标吗
y
x
A
解:建立直角坐标系如右图,选择比例为1:10,取点A为直角坐标系的原点,线段AB在X轴上,则可得A、B、C、D各点的坐标分别为:
3
2
1
3
4
2
1
B(3,0)
4
C(3.5,1.5)
(0,0)
D(1,3.5)
如上图中的四边形ABCD就是所求作的图形
用线段依次连结各点
3.如图,矩形ABCD的长与宽分别为6,4,建立适当的直角坐标系,并写出各个顶点的坐标
A
B
C
D
由AB 的长6,AD的长为4,可以得到B,D,C的坐标为B(6,0),D(0,4),C(6,4)
x
y
解:如图:以A为坐标原点,分别
以AB,AD所在的直线为X轴,Y轴,
建立直角坐标系。此时的点A的坐标
为(0,0)
你还可以怎样建立直角坐标系呢?
A
B
C
D
解:如图:以AB所在的直线为X轴,以线段AB的中垂线为Y轴,建立直角坐标系。
由AB的长6,此时的点A的坐
标为(-3,0), B(3,0)
AD的长为4,可以得到D,C的坐标
为D(-3,4),C(3,4)
x
y
O
解:以线段AD的中垂线为x轴,线段AB的中垂线为y轴,建立平面直角坐标系
由于线段AB长为6,线段AD长为4,
则各点的坐标分别为
A(-3,-2)、B(3,-2)、C(3,2)、D(-3,2)
x
y
O
A
B
C
D
要确定某点的位置在于, 建立适当的直角坐标系。
1.选择适当的点作为原点;(充分利用特殊点)
2.适当的直线作为坐标轴(充分利用特殊边)
3.选择适当的距离为单位长度。
(一般按比例选择)
归 纳
1.若以点B为原点建立平面直角坐标系,点A的坐标为( 3 , 4 ),若以点A为原点建立平面直角坐标系,则点 B 的坐标可能是( )
A .(-3 ,-4) B .(-3 ,4) C .(3 ,-4) D .(3, 4)
1
1
2
3
4
-1
-2
-3
-4
2
3
4
-1
-2
-3
-4
0
A
B
A
当堂检测:
夯实基础,稳扎稳打
2.如图所示,在象棋盘上建立平面直角坐标系,若“帅”位于点(-1,-2),
“马”位于点(2 ,-2),则“兵”位于点( )
A .(- 1 , 1) B .(- 2 ,- 1)
C .(- 3 , 1) D .( 1 ,- 2)
C
x
y
o
A
B
C
A
B
C
x
y
o
D
┗
2
2
┒
3.等边 △ABC的边长为 2,建立适当的直角坐标系,并求等边 △ABC各个顶点的坐标
法1:BD=1,AD=
.
A(1,)
B(0,0)
C(2,0)
法2:C0=1,A0=
A(0,)
B(-1,0)
C(1,0)
A
B
C
x
y
o
x
y
o
A
B
C
等边 △ABC的边长为 2,建立适当的直角坐标系,并求等边 △ABC各个顶点的坐标
D
┗
2
2
┒
D
法3:CD=1,AD=
.
A(-1,)
B(-2,0)
C(0,0)
法4:CD=1,AD=
.
B(-1,)
A(0,0)
C(1,)
A
B
C
4.腰长为2的等腰Rt△ABC,建立适当的直角坐标系,并写出各顶点的坐标
x
y
O
A
B
C
x
y
O
D
┗
法1:BD=AD=CD=
.
A(,)
B(0,0)
C(2,0)
┛
法2:B0=AD=CD=
.
A(0,)
B(-,0)
C(,0)
A
B
C
A
B
C
x
y
O
x
y
O
腰长为2的等腰Rt△ABC,建立适当的直角坐标系,并写出各顶点的坐标
D
┗
法3:BD=AD=CD=
.
A(,)
C(0,0)
B(-2,0)
法3:BD=AD=CD=
.
B(,)
A(0,0)
C()
┒
D
A
B
C
A
B
C
5.腰长为2、顶角为1200的等腰△ABC,建立适当的直角坐标系,并写出各顶点的坐标
1200
2
2
1200
x
y
O
x
y
O
D
┛
┛
法1:BD=CD=
.AD=1
A(,1)
B(0,0)
C(2,0)
法2:BO=CO=
.AO=1
C(,0)
A(0,1)
B(,0)
A
B
C
A
B
C
2
2
腰长为2、顶角为1200的等腰△ABC,建立适当的直角坐标系,并写出各顶点的坐标
1200
1200
x
y
O
x
y
O
D
┛
法3:BD=CD=
.AD=1
A(,1)
B(,0)
C(0,0)
法4:BD=CD=
.AD=1
┛
D
B(,-1)
C(,1)
A(0,0)
x
y
O
6.Rt△ABC,AB=6,BC=8,在直角坐标系中的位置如图,写出各顶点的坐标
A
B
┛
c
OA=
.
A(10 , 0)
C(0 , 0)
┛
D
6×8=10×BD
BD=4.8
OD=
.
=
.
=
.
=
.
=6.4
B(6.4 , 4.8)
连续递推,豁然开朗
A
B
C
D
∵∠AOB=90°,∴∠AOC+∠BOD=90°.
∵∠AOC+∠OAC=90°,
∴∠OAC=∠BOD.
在△AOC与△BOD中
∴△AOC≌△OBD(AAS).
∴AC=OD, OC=BD
7.如图,△AOB在直角坐标系中,∠AOB=90°,OA=OB,若A(-2 , 3),
点B的坐标和△ABC的面积.
解:分别过A、B作AC⊥轴于C,BD⊥轴于D,
.
.
∵A(-2 , 3)
∴AC=OD=3, OC=BD=2
∴B(3 , 2)
在Rt△AOC中,OA2=OC2+AC2=13,
∴AC=.
.
∴AC=BC= , S△AOB=
.
.
开心图形(K型图)藏其中
8.如图是传说中的一张藏宝岛图,藏宝人生前通过建立直角坐标系(以南北方向为纵轴,东西方向为横轴)画出这幅藏宝图,现在我们只知道图上两块大石头的坐标为A(1,2),B(8,9),而藏宝地的坐标为(5,7),试设法在地图上找到宝藏,并表示出来。
解:根据A、B两点的坐标,可确定原来的坐标系如图
x
y
0
2
4
8
10
6
10
8
6
2
4
A(1,2)
B(8,9)
C(5,7)
图中的点C即藏宝地.
A(1,2)
B(8,9)
D
水平线AD与铅直线BD-----直角
等腰Rt△ABD-----单位长度1
A(1,2)-------坐标原点
藏宝图--------等腰直角三角形藏其中
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
