4.3.2 坐标平面内图形的平移 课件(共21张PPT)
文档属性
| 名称 | 4.3.2 坐标平面内图形的平移 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-09 11:25:01 | ||
图片预览






文档简介
(共21张PPT)
4.3.2坐标平面内图形的平移
浙教版 八年级上册
教学目标
【教学目标】
1.从点运动的过程,培养学生由特例发现问题的一般规律性的能力。
2.在点的运动到线段平移到图形的变换的过程中,学会有条理地思考并进行演绎推理。
3.通过对问题的共同探讨,培养学生的合作精神。
【重点】点平移时坐标的变化规律。
【难点】由点的平移到图形的变换的演绎过程。
复习回顾
在平面内,把一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移.
问题1 什么叫平移吗?
问题2 图形平移的性质是什么?
1.新图形与原图形形状和大小不变,但位置改变;
2.对应点的连线平行(或共线)且相等.
3.对应线段平行(或共线)且相等,对应角相等.
A
B
C
D
E
F
合作探究
A·
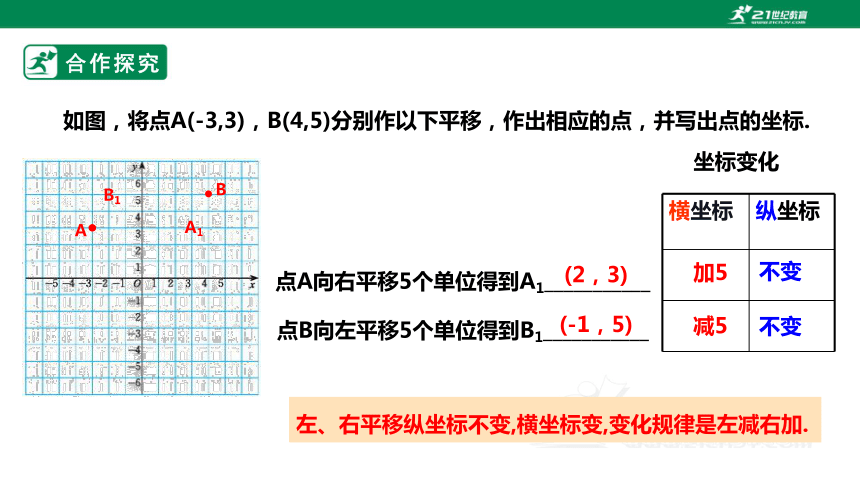
如图,将点A(-3,3),B(4,5)分别作以下平移,作出相应的点,并写出点的坐标.
点A向右平移5个单位得到A1___________
(2,3)
A1
·
·
点B向左平移5个单位得到B1___________
(-1,5)
·
B
B1
横坐标 纵坐标
坐标变化
加5
减5
不变
不变
左、右平移纵坐标不变,横坐标变,变化规律是左减右加.
合作探究
A·
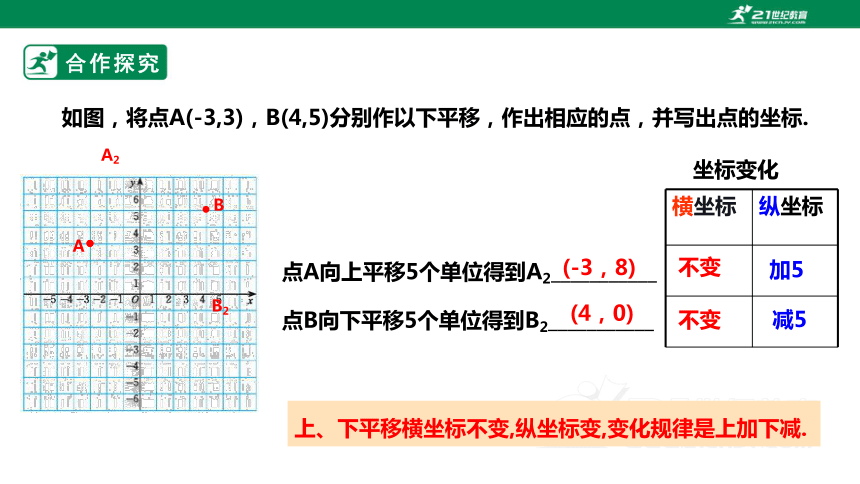
如图,将点A(-3,3),B(4,5)分别作以下平移,作出相应的点,并写出点的坐标.
点A向上平移5个单位得到A2___________
(-3,8)
A2
·
·
点B向下平移5个单位得到B2___________
(4,0)
·
B
B2
横坐标 纵坐标
坐标变化
不变
不变
加5
减5
上、下平移横坐标不变,纵坐标变,变化规律是上加下减.
合作探究
比较各点平移时的坐标变化,填在表格内.
你能发现点平移时坐标变化的规律吗?
A(-3,3)
B(4,5)
A(-3,3)
B(4,5)
向右平移5个单位
(2,3)
向左平移5个单位
(-1,5)
向上平移5个单位
(-3,8)
向下平移5个单位
(4,0)
横坐标 纵坐标
加5
不变
减5
不变
不变
加5
不变
减5
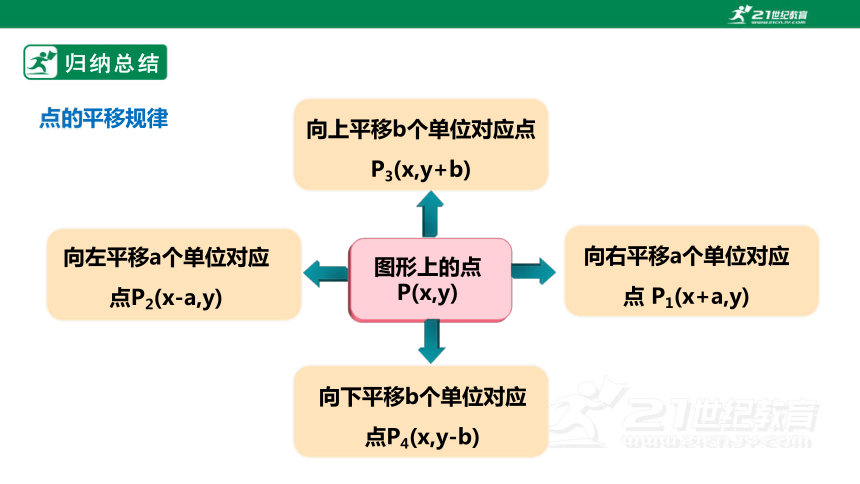
归纳总结
向上平移b个单位对应点P3(x,y+b)
向左平移a个单位对应点P2(x-a,y)
图形上的点P(x,y)
向下平移b个单位对应点P4(x,y-b)
向右平移a个单位对应点 P1(x+a,y)
点的平移规律
做一做
1.已知点A的坐标为(-2,-3),分别求点A经下列平移后所得的点的坐标。
(1)向上平移3个单位
(3)向左平移2个单位
(-2, 0)
(-2, -6)
(-4,-3)
(2,-3)
(2)向下平移3个单位
(4)向右平移4个单位
2.已知点A的坐标为(a,b),点A经怎样平移得到下列点
(1) (a-2,b).
(2)(a,b+2).
向左平移2个单位
向上平移2个单位
方法总结
(1)原图形向左(右)平移a个单位长度:(a>0)
向右平移a个单位
(2)原图形向上(下)平移b个单位长度:(b>0)
原图形上的点P(x,y)
向左平移a个单位
原图形上的点P (x,y)
P1(x+a,y)
P2(x-a,y)
向上平移b个单位
原图形上的点P(x,y)
向下平移b个单位
原图形上的点P(x,y)
P3(x,y+b)
P4(x,y-b)
例题讲解
例2 如图,在直角坐标系中,平行于x轴的线段AB上所有点的纵坐标都是-1,横坐标x的取值范围是1≤x ≤5 ,则线段AB上任意一点的坐标可以用“(x,-1) (1≤x≤5)” 表示,按照类似这样的规定,回答下面的问题:
C
D
A
B
1.怎样表示线段CD上任意一点的坐标?
(2, y)(-1≤y≤3)
例题讲解
2.把线段AB向上平移2.5个单位,作出所得的线段A‘B’.线段A‘B’上任意一点的坐标怎样表示?
C
D
A
B
(x, 1.5)(1≤x ≤5)
A'
B'
3.把线段CD向左平移3个单位,作出所得的线段C‘D’.线段C‘D’上任意一点的坐标怎样表示?
(-1, y)(-1≤y ≤3)
C'
D'
例题讲解
例3 如图.
(1)分别求出点A,A'和点B,B'的坐标,并比较A与A',B与B'之间的坐标变化.
(2)图甲怎样平移到图乙
例题讲解
解 (1)点A,A'的坐标分别为A(-8,-1),A'(-3,4);点B,B'的坐标分别为B(-3,-1),B'(2,4). 由A到A',横坐标增加5,纵坐标增加5;由B到B',横坐标增加5,纵坐标增加5.
(2)由第(1)题知,A,B都向右平移5个单位,向上平移5个单位.从图甲到图乙,可以看做经过了两次平移:一次是向右平移5个单位,另一次是向上平移5个单位.
归纳总结
图形在坐标平面中的平移:
指在坐标系中,在保持坐标轴不动的情况下,图形的整体移动.
在平面直角坐标系中,对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化;
反过来,从图形上的点的坐标变化,也可以得出这个图形进行了怎样的平移.
一个图形依次沿x轴方向、y轴方向平移后所得图形与原来的图形相比,位置有什么变化?它们对应点的坐标之间有怎样的关系?
平移方向和平移距离 对应点的坐标
向右平移a个单位长度,向上平移b个单位长度
向右平移a个单位长度,向下平移b个单位长度
向左平移a个单位长度,向上平移b个单位长度
向左平移a个单位长度,向下平移b个单位长度
(x+a , y+b)
(x+a , y-b)
(x-a , y+b)
(x-a , y-b)
归纳总结
课堂练习
1.在平面直角坐标系中,将点P(3,1)向下平移2个单位长度,得到的点P′的坐标为( )
A.(3,-1) B.(3,3) C.(1,1) D.(5,1)
2.如图,在平面直角坐标系中,已知点A(2,1),点B(3,-1),平移线段AB,使点A落在点A1(-2,2)处,则点B的对应点B1的坐标为( )
A.(-1,-1) B.(1,0)
C.(-1,0) D.(3,0)
A
C
课堂练习
3.将点A(3,2)向上平移2个单位长度,得到A1,则A1的坐标为______.
将点A(3,2)向下平移3个单位长度,得到A2,则A2的坐标为______.
将点A(3,2)向左平移4个单位长度,得到A3,则A3的坐标为______.
(3,4)
4.点A1(6,3)是由点A(-2,3)经过 得到的,点B(4,3)向 得到B1(6,3).
向右平移8个单位长度
右平移2个单位长度
(3,-1)
(-1,2)
课堂练习
5.如图,请写出平行四边形ABCD各顶点的坐标,将此图形先向上平移2个单位长度,再向左平移1个单位长度得到对应图形EFGH,写出EFGH各顶点的坐标,这个四边形是平行四边形吗?
解:A(-2,1), B(1,1), C(3,-1),D(0,-1);E(-3,3), F(0,3),G(2,1), H(-1,1),
这个四边形是平行四边形.
课堂总结
图形在坐标系中的平移
沿x轴
平移
沿y轴
平移
纵坐标不变
向右平移,横坐标加上一个正数
向左平移,横坐标减去一个正数
横坐标不变
向上平移,纵坐标加上一个正数
向下平移,纵坐标减去一个正数
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
4.3.2坐标平面内图形的平移
浙教版 八年级上册
教学目标
【教学目标】
1.从点运动的过程,培养学生由特例发现问题的一般规律性的能力。
2.在点的运动到线段平移到图形的变换的过程中,学会有条理地思考并进行演绎推理。
3.通过对问题的共同探讨,培养学生的合作精神。
【重点】点平移时坐标的变化规律。
【难点】由点的平移到图形的变换的演绎过程。
复习回顾
在平面内,把一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移.
问题1 什么叫平移吗?
问题2 图形平移的性质是什么?
1.新图形与原图形形状和大小不变,但位置改变;
2.对应点的连线平行(或共线)且相等.
3.对应线段平行(或共线)且相等,对应角相等.
A
B
C
D
E
F
合作探究
A·
如图,将点A(-3,3),B(4,5)分别作以下平移,作出相应的点,并写出点的坐标.
点A向右平移5个单位得到A1___________
(2,3)
A1
·
·
点B向左平移5个单位得到B1___________
(-1,5)
·
B
B1
横坐标 纵坐标
坐标变化
加5
减5
不变
不变
左、右平移纵坐标不变,横坐标变,变化规律是左减右加.
合作探究
A·
如图,将点A(-3,3),B(4,5)分别作以下平移,作出相应的点,并写出点的坐标.
点A向上平移5个单位得到A2___________
(-3,8)
A2
·
·
点B向下平移5个单位得到B2___________
(4,0)
·
B
B2
横坐标 纵坐标
坐标变化
不变
不变
加5
减5
上、下平移横坐标不变,纵坐标变,变化规律是上加下减.
合作探究
比较各点平移时的坐标变化,填在表格内.
你能发现点平移时坐标变化的规律吗?
A(-3,3)
B(4,5)
A(-3,3)
B(4,5)
向右平移5个单位
(2,3)
向左平移5个单位
(-1,5)
向上平移5个单位
(-3,8)
向下平移5个单位
(4,0)
横坐标 纵坐标
加5
不变
减5
不变
不变
加5
不变
减5
归纳总结
向上平移b个单位对应点P3(x,y+b)
向左平移a个单位对应点P2(x-a,y)
图形上的点P(x,y)
向下平移b个单位对应点P4(x,y-b)
向右平移a个单位对应点 P1(x+a,y)
点的平移规律
做一做
1.已知点A的坐标为(-2,-3),分别求点A经下列平移后所得的点的坐标。
(1)向上平移3个单位
(3)向左平移2个单位
(-2, 0)
(-2, -6)
(-4,-3)
(2,-3)
(2)向下平移3个单位
(4)向右平移4个单位
2.已知点A的坐标为(a,b),点A经怎样平移得到下列点
(1) (a-2,b).
(2)(a,b+2).
向左平移2个单位
向上平移2个单位
方法总结
(1)原图形向左(右)平移a个单位长度:(a>0)
向右平移a个单位
(2)原图形向上(下)平移b个单位长度:(b>0)
原图形上的点P(x,y)
向左平移a个单位
原图形上的点P (x,y)
P1(x+a,y)
P2(x-a,y)
向上平移b个单位
原图形上的点P(x,y)
向下平移b个单位
原图形上的点P(x,y)
P3(x,y+b)
P4(x,y-b)
例题讲解
例2 如图,在直角坐标系中,平行于x轴的线段AB上所有点的纵坐标都是-1,横坐标x的取值范围是1≤x ≤5 ,则线段AB上任意一点的坐标可以用“(x,-1) (1≤x≤5)” 表示,按照类似这样的规定,回答下面的问题:
C
D
A
B
1.怎样表示线段CD上任意一点的坐标?
(2, y)(-1≤y≤3)
例题讲解
2.把线段AB向上平移2.5个单位,作出所得的线段A‘B’.线段A‘B’上任意一点的坐标怎样表示?
C
D
A
B
(x, 1.5)(1≤x ≤5)
A'
B'
3.把线段CD向左平移3个单位,作出所得的线段C‘D’.线段C‘D’上任意一点的坐标怎样表示?
(-1, y)(-1≤y ≤3)
C'
D'
例题讲解
例3 如图.
(1)分别求出点A,A'和点B,B'的坐标,并比较A与A',B与B'之间的坐标变化.
(2)图甲怎样平移到图乙
例题讲解
解 (1)点A,A'的坐标分别为A(-8,-1),A'(-3,4);点B,B'的坐标分别为B(-3,-1),B'(2,4). 由A到A',横坐标增加5,纵坐标增加5;由B到B',横坐标增加5,纵坐标增加5.
(2)由第(1)题知,A,B都向右平移5个单位,向上平移5个单位.从图甲到图乙,可以看做经过了两次平移:一次是向右平移5个单位,另一次是向上平移5个单位.
归纳总结
图形在坐标平面中的平移:
指在坐标系中,在保持坐标轴不动的情况下,图形的整体移动.
在平面直角坐标系中,对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化;
反过来,从图形上的点的坐标变化,也可以得出这个图形进行了怎样的平移.
一个图形依次沿x轴方向、y轴方向平移后所得图形与原来的图形相比,位置有什么变化?它们对应点的坐标之间有怎样的关系?
平移方向和平移距离 对应点的坐标
向右平移a个单位长度,向上平移b个单位长度
向右平移a个单位长度,向下平移b个单位长度
向左平移a个单位长度,向上平移b个单位长度
向左平移a个单位长度,向下平移b个单位长度
(x+a , y+b)
(x+a , y-b)
(x-a , y+b)
(x-a , y-b)
归纳总结
课堂练习
1.在平面直角坐标系中,将点P(3,1)向下平移2个单位长度,得到的点P′的坐标为( )
A.(3,-1) B.(3,3) C.(1,1) D.(5,1)
2.如图,在平面直角坐标系中,已知点A(2,1),点B(3,-1),平移线段AB,使点A落在点A1(-2,2)处,则点B的对应点B1的坐标为( )
A.(-1,-1) B.(1,0)
C.(-1,0) D.(3,0)
A
C
课堂练习
3.将点A(3,2)向上平移2个单位长度,得到A1,则A1的坐标为______.
将点A(3,2)向下平移3个单位长度,得到A2,则A2的坐标为______.
将点A(3,2)向左平移4个单位长度,得到A3,则A3的坐标为______.
(3,4)
4.点A1(6,3)是由点A(-2,3)经过 得到的,点B(4,3)向 得到B1(6,3).
向右平移8个单位长度
右平移2个单位长度
(3,-1)
(-1,2)
课堂练习
5.如图,请写出平行四边形ABCD各顶点的坐标,将此图形先向上平移2个单位长度,再向左平移1个单位长度得到对应图形EFGH,写出EFGH各顶点的坐标,这个四边形是平行四边形吗?
解:A(-2,1), B(1,1), C(3,-1),D(0,-1);E(-3,3), F(0,3),G(2,1), H(-1,1),
这个四边形是平行四边形.
课堂总结
图形在坐标系中的平移
沿x轴
平移
沿y轴
平移
纵坐标不变
向右平移,横坐标加上一个正数
向左平移,横坐标减去一个正数
横坐标不变
向上平移,纵坐标加上一个正数
向下平移,纵坐标减去一个正数
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
