2.2一元二次方程的解法(1)[下学期]
文档属性
| 名称 | 2.2一元二次方程的解法(1)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 117.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-01 00:00:00 | ||
图片预览





文档简介
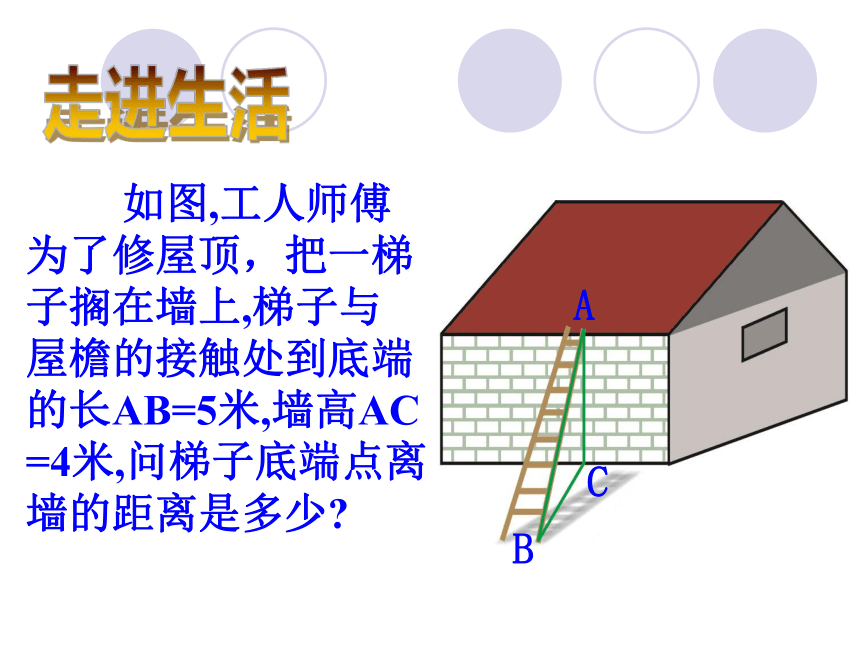
课件16张PPT。一元二次方程的解法(一)1 .x2-4=0; 2.(x+1)2-25=0.解:(x+2)(x-2)=0,∴x+2=0,或x-2=0.∴x1=-2, x2=2.你能用因式分解法解下列方程吗?解:[(x+1)+5][(x+1)-5]=0,∴x+6=0,或x-4=0.∴x1=-6, x2=4.这两个方程是否还有其它的解法?思考 如图,工人师傅
为了修屋顶,把一梯
子搁在墙上,梯子与
屋檐的接触处到底端
的长AB=5米,墙高AC
=4米,问梯子底端点离
墙的距离是多少?ABC走进生活设BC=x,根据勾股定理,得 x2+42=52.
化简,得 x2-9=0,
∴ (x-3) (x+3) =0,
解得x1=3,x2=-3 (不合题意,舍去).
另解:x2=9,
∴x1= =3,
X2=- =-3 (不合题意,舍去). 一般地,对于形如x2=a(a≥0)的方程,
根据平方根的定义,可解得
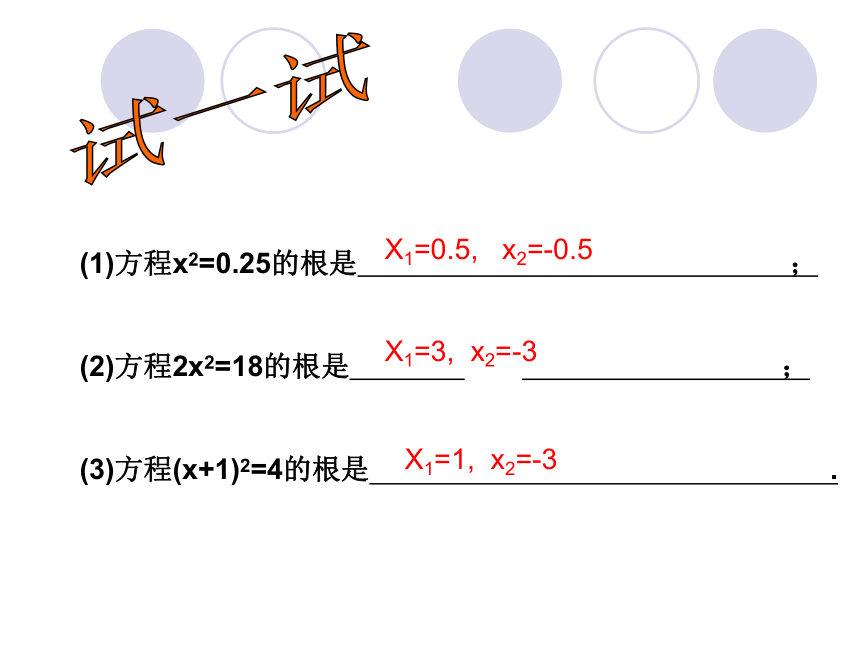
这种解一元二次方程的方法叫做开平方法.概念试一试(1)方程x2=0.25的根是 ;
(2)方程2x2=18的根是 ;
(3)方程(x+1)2=4的根是 . X1=0.5, x2=-0.5X1=3, x2=-3X1=1, x2=-3解一解用开平方法解下列方程:
(1)3x2-27=0;
(2)(x+1)2=4
(3)(2x-3)2=7
(4)x2+2 x+5=0你能用开平方法解下列方程吗?
x2-10x+16=0合作探究这种方程怎样解?变形为变形为x2-10x+25=9x2-10x+16=0的形式.(a为非负常数) 把一元二次方程的左边配成一个完全
平方式,右边为一个非负常数,然后用
开平方法求解,这种解一元二次方程的方法
叫做配方法.概念(1)x2+8x+ =(x+4)2
(2)x2-3x+ =(x- )2
(3)x2-12x+ =(x- )2填空配方时,配上的是一次项系数一半的平方.42 ( )2626用配方法解方程x2+12x=-9你能总结出配方法的步骤吗?解:方程的两边都加上36,得X2+12x+36=-9+36即 (x+6)2=27. ∴x+6= 或x+6=- 解得 x1=-6+3 ,x2=-6-3 解得 x1=-6+3 ,x2=-6-3 解得 x1=-6+3 ,x2=-6-3 解得 x1=-6+3 ,x2=-6-3 解得 x1=-6+3 ,x2=-6-3 解得 x1=-6+3 ,x2=-6-3 ∴x+6= 或x+6=- 解得 x1=-6+3 ,x2=-6-3 解得 x1=-6+3 ,x2=-6-3 解得 x1=-6+3 ,x2=-6-3 解得 x1=-6+3 ,x2=-6-3 解得 x1=-6+3 ,x2=-6-3 用配方法解一元二次方程的步骤:移项:把常数项移到方程的右边;
配方:方程两边都加上一次项系数
一半的平方;
开方:根据平方根意义,方程两边开平方;
求解:解一元一次方程;
定解:写出原方程的解.做一做用配方法解下列方程:
(1)x2+6x=1
(2)x2=6-5x
(3) -x2+4x-3=0注意:解第(2)题时要先移项,变形成x2+5x=6的形式;
如果方程的二次项系数为负,则先把二次项系数化为正.小结说一说你今天学到了什么?作业1.作业本;
2.课后作业选做.
为了修屋顶,把一梯
子搁在墙上,梯子与
屋檐的接触处到底端
的长AB=5米,墙高AC
=4米,问梯子底端点离
墙的距离是多少?ABC走进生活设BC=x,根据勾股定理,得 x2+42=52.
化简,得 x2-9=0,
∴ (x-3) (x+3) =0,
解得x1=3,x2=-3 (不合题意,舍去).
另解:x2=9,
∴x1= =3,
X2=- =-3 (不合题意,舍去). 一般地,对于形如x2=a(a≥0)的方程,
根据平方根的定义,可解得
这种解一元二次方程的方法叫做开平方法.概念试一试(1)方程x2=0.25的根是 ;
(2)方程2x2=18的根是 ;
(3)方程(x+1)2=4的根是 . X1=0.5, x2=-0.5X1=3, x2=-3X1=1, x2=-3解一解用开平方法解下列方程:
(1)3x2-27=0;
(2)(x+1)2=4
(3)(2x-3)2=7
(4)x2+2 x+5=0你能用开平方法解下列方程吗?
x2-10x+16=0合作探究这种方程怎样解?变形为变形为x2-10x+25=9x2-10x+16=0的形式.(a为非负常数) 把一元二次方程的左边配成一个完全
平方式,右边为一个非负常数,然后用
开平方法求解,这种解一元二次方程的方法
叫做配方法.概念(1)x2+8x+ =(x+4)2
(2)x2-3x+ =(x- )2
(3)x2-12x+ =(x- )2填空配方时,配上的是一次项系数一半的平方.42 ( )2626用配方法解方程x2+12x=-9你能总结出配方法的步骤吗?解:方程的两边都加上36,得X2+12x+36=-9+36即 (x+6)2=27. ∴x+6= 或x+6=- 解得 x1=-6+3 ,x2=-6-3 解得 x1=-6+3 ,x2=-6-3 解得 x1=-6+3 ,x2=-6-3 解得 x1=-6+3 ,x2=-6-3 解得 x1=-6+3 ,x2=-6-3 解得 x1=-6+3 ,x2=-6-3 ∴x+6= 或x+6=- 解得 x1=-6+3 ,x2=-6-3 解得 x1=-6+3 ,x2=-6-3 解得 x1=-6+3 ,x2=-6-3 解得 x1=-6+3 ,x2=-6-3 解得 x1=-6+3 ,x2=-6-3 用配方法解一元二次方程的步骤:移项:把常数项移到方程的右边;
配方:方程两边都加上一次项系数
一半的平方;
开方:根据平方根意义,方程两边开平方;
求解:解一元一次方程;
定解:写出原方程的解.做一做用配方法解下列方程:
(1)x2+6x=1
(2)x2=6-5x
(3) -x2+4x-3=0注意:解第(2)题时要先移项,变形成x2+5x=6的形式;
如果方程的二次项系数为负,则先把二次项系数化为正.小结说一说你今天学到了什么?作业1.作业本;
2.课后作业选做.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
