一元二次方程的应用（1）[下学期]

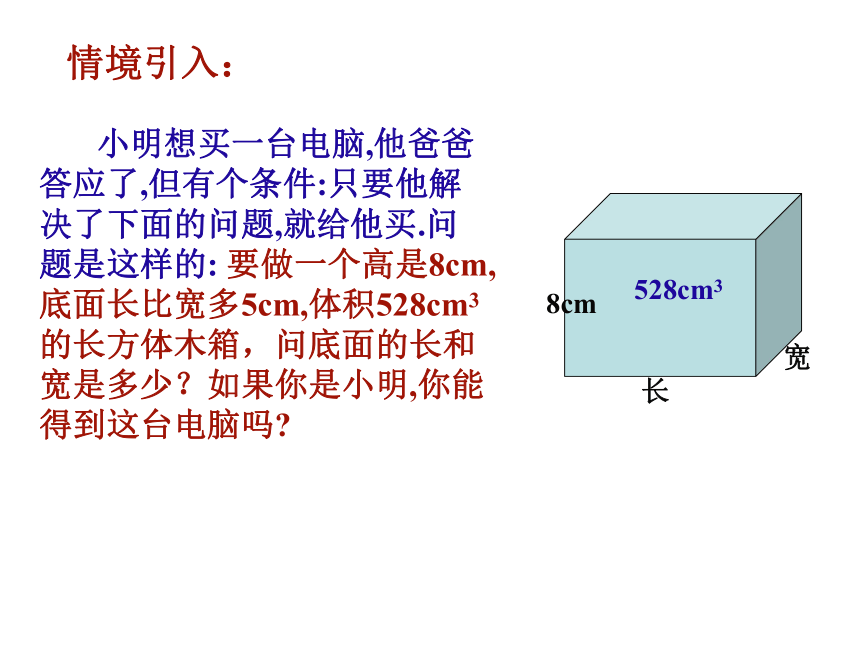
课件20张PPT。浙教版八年级数学（下册）2.3 一元二次方程的应用（1）情境引入： 小明想买一台电脑,他爸爸答应了,但有个条件:只要他解决了下面的问题,就给他买.问题是这样的: 要做一个高是8cm,底面长比宽多5cm,体积528cm3的长方体木箱，问底面的长和宽是多少？如果你是小明,你能得到这台电脑吗?解：设长方体的宽为x(cm),则长为______cm,底面积为_______cm.长方体的底面积×高=长方体体积(528cm)列方程：化简、整理后，得解得 x1=-11,x2=6检验：x1=-11＜0不符合实际情况,舍去.
当x2=6时,符合题意∴x=6∴长方体的长为6+5=11答:长方体的宽为6cm,长为11cm.找相等关系：(x+5)x(x+5)x(x+5) ×8=528x2+5x-66=0
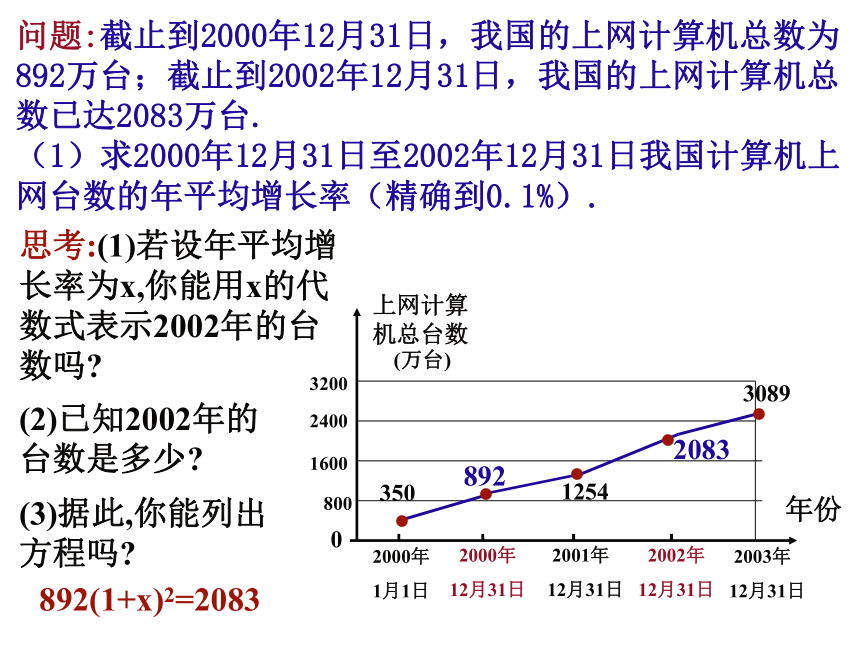
回顾：列方程解应用题的基本步骤怎样？ 找出题中的量，分清有哪些已知量、未知 量，哪些是要求的未知量和所涉及的基本数量关系、相等关系； 设元，包括设直接未知数或间接未知数；用所设的未知数字母的代数式表示其他的相关量；列方程(一元二次方程)；解方程；注意根的准确性及是否符合实际意义。（1）审题：（2）设：（3）列：（5）检验并作答：（4）解：问题: 某花圃用花盆培育某种花苗,经过试验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株?如果直接设每盆植x株,怎样表示问题中相关的量?解:设每盆花苗增加的株数为x株,则每盆花苗有______株,平均单株盈利为__________元.相等关系:平均单株盈利×株数=10元由题意,得(x+3)(3-0.5x)=10解这个方程,得:x1=1, x2=2(x+3)(3-0.5x)如果设每盆花苗增加的株数为x株呢？思考:这个问题设什么为x?有几种设法?化简，整理，得 x2-3x+2=0经检验，x1=1,x2=2都是方程的解，且符合题意.答:要使每盆的盈利达到10元,每盆应植入4株或5株.练一练:1.已知两个连续正奇数的积是63,利用一元二次方程求这两个数.问题:截止到2000年12月31日，我国的上网计算机总数为892万台；截止到2002年12月31日，我国的上网计算机总数已达2083万台.
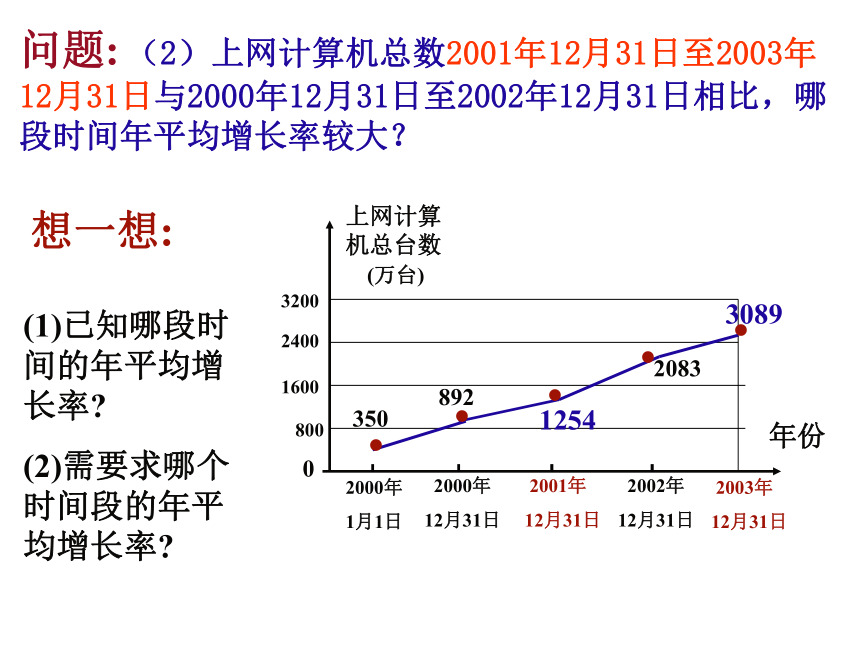
（1）求2000年12月31日至2002年12月31日我国计算机上网台数的年平均增长率（精确到0.1%）.思考:(1)若设年平均增长率为x,你能用x的代数式表示2002年的台数吗?(2)已知2002年的台数是多少?(3)据此,你能列出方程吗?892(1+x)2=2083问题: （2）上网计算机总数2001年12月31日至2003年12月31日与2000年12月31日至2002年12月31日相比，哪段时间年平均增长率较大？(1)已知哪段时间的年平均增长率?
(2)需要求哪个时间段的年平均增长率?想一想:网上有这样一则消息： 系列特许商品自去年11月1日在北京一亮相，就出现了抢购热潮。北京贵友大厦去年十一月份售出了10万套吉祥物毛绒玩具，而今年一月份则售出了16.9万套，问平均每月增长的百分率是多少？福娃练一练: 某校坚持对学生进行近视眼的防治,近视学生人数逐年减少.据统计,今年的近视学生人数是前年人数的75℅,那么这两年平均每年近视学生人数降低的百分率是多少(精确到1℅)? 宁波港是一个多功能、综合性的现代化大港，年货物吞吐量位于中国大陆第二，世界排名第五，成功跻身于国际大港行列.如图是宁波港1994年～2004年货物吞吐统计图.
（1）统计图中
你能发现哪些
信息，请说出
两个；
课题学习:（2）有人断定宁波港货物吞吐量的年平均增长率不超过15%，你认为他的说法正确吗？请你说明理由.
谈一谈:通过本课的学习,你有什么收获?布置作业:(1)课本38页作业题;
(2)作业本. 学校图书馆去年年底有图书5万册，预计到明年年底增加到7.2万册.求这两年的年平均增长率. 某市进行环境绿化，计划两年内把绿化面积增加44%，问平均每年增长的百分率是多少？ 某种药剂原售价为4元, 经过两次降价, 现在每瓶售价为2.56元,问平均每次降价百分之几? 某公司计划经过两年把某种商品的生产成本降低19%，那么平均每年需降低百分之几? 某单位为节省经费,在两个月内将开支从每月1600元降到900元,求这个单位平均每月降低的百分率是多少?