4.5.1相似三角形的性质及应用 课件(共25张PPT)
文档属性
| 名称 | 4.5.1相似三角形的性质及应用 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 00:00:00 | ||
图片预览


文档简介
(共25张PPT)
4.5.1相似三角形的性质及应用
浙教版 九年级上册
教学目标
教学目标:
1.经历相似三角形性质“相似三角形对应高线、对应中线、对应角平分线之比等于相似比.
巩固相似三角形性质,并能熟练运用.
重点:相似三角形的性质及对应线段的性质.
难点:掌握相似三角形性质的应用.
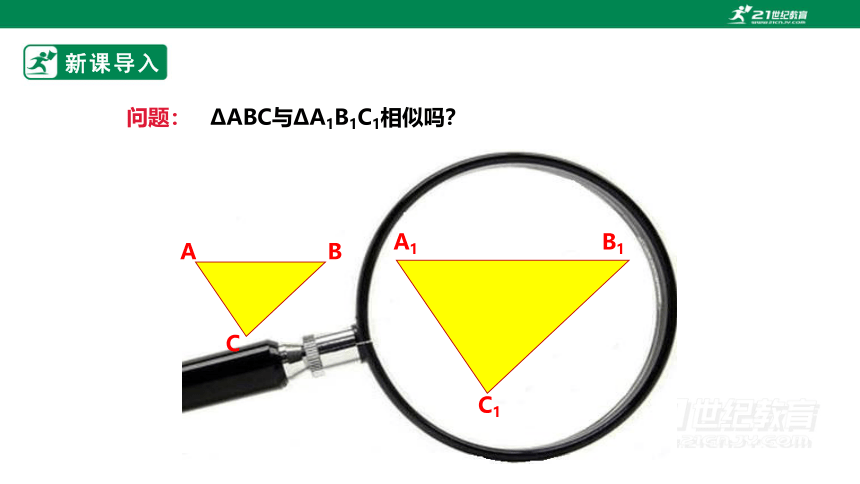
新课导入
A
C
B
A1
C1
B1
问题: ΔABC与ΔA1B1C1相似吗?
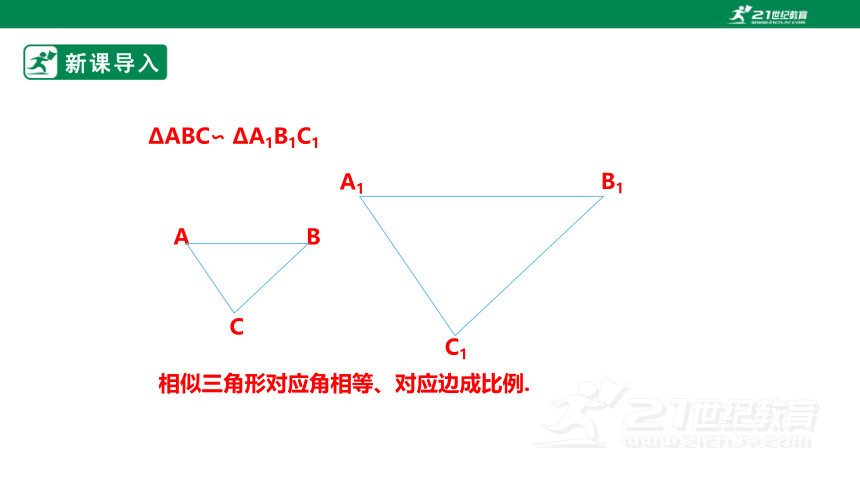
新课导入
A
C
B
A1
C1
B1
相似三角形对应角相等、对应边成比例.
ΔABC∽ ΔA1B1C1
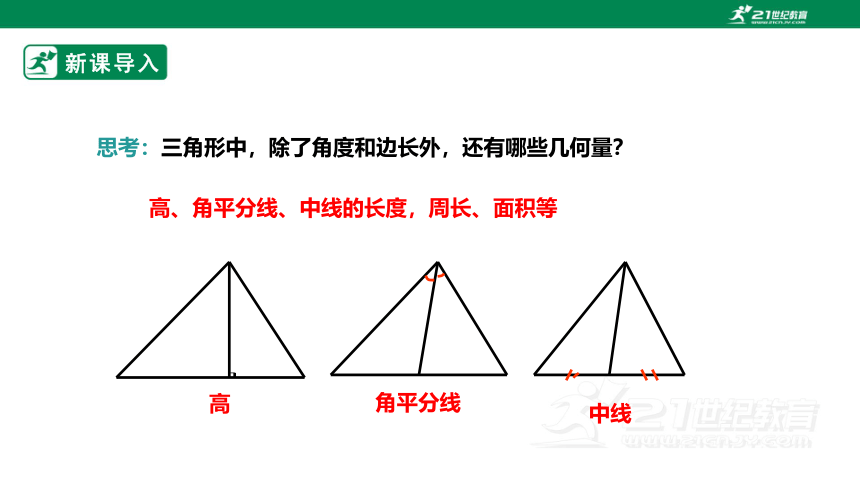
新课导入
思考:三角形中,除了角度和边长外,还有哪些几何量?
高、角平分线、中线的长度,周长、面积等
高
角平分线
中线
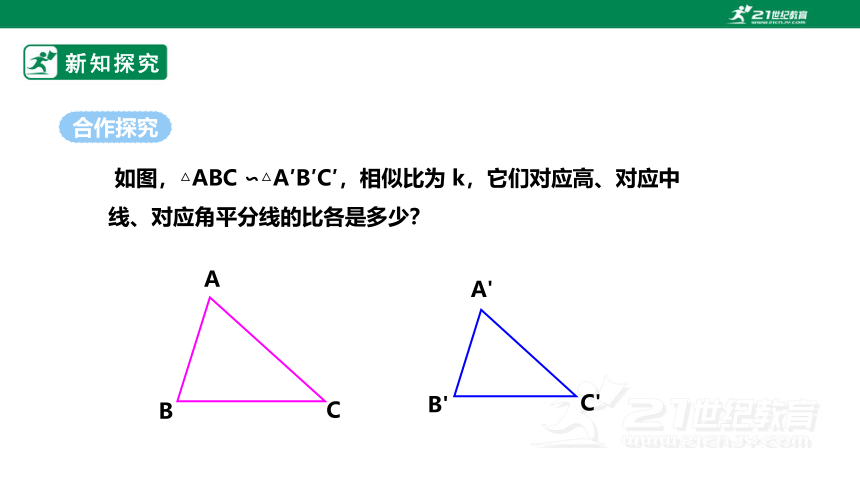
新知探究
合作探究
如图,△ABC ∽△A′B′C′,相似比为 k,它们对应高、对应中线、对应角平分线的比各是多少?
A
B
C
A'
B'
C'
新知探究
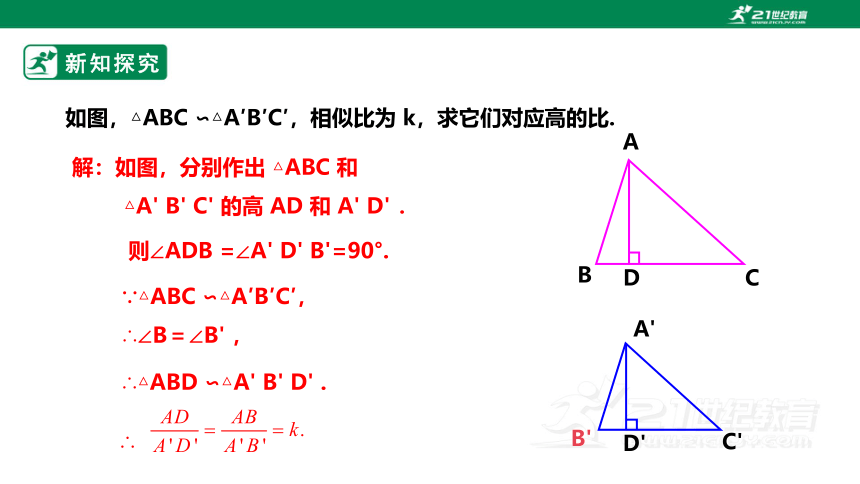
∵△ABC ∽△A′B′C′,
∴∠B=∠B' ,
解:如图,分别作出 △ABC 和
△A' B' C' 的高 AD 和 A' D' .
则∠ADB =∠A' D' B'=90°.
∴△ABD ∽△A' B' D' .
A
B
C
A'
B'
C'
D'
D
∴
如图,△ABC ∽△A′B′C′,相似比为 k,求它们对应高的比.
新知探究
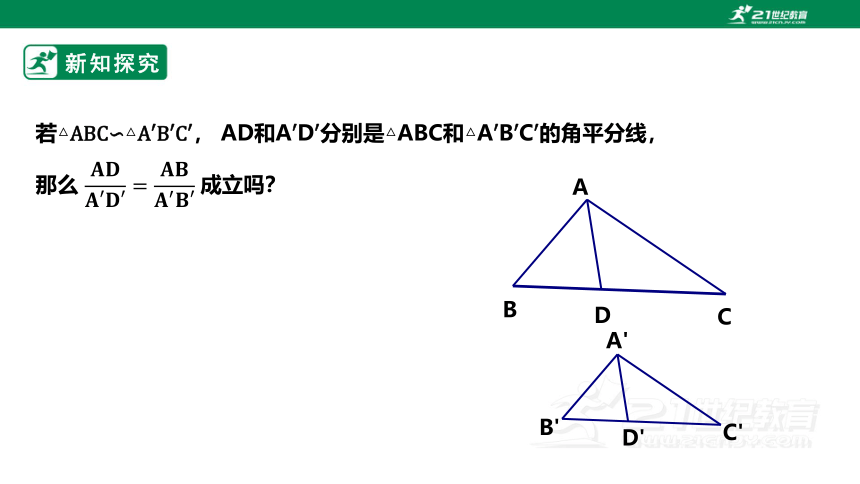
若△△, AD和AD分别是△ABC和△ABC的角平分线,
那么 成立吗?
D'
A'
B'
C'
D
A
B
C
新知探究
D'
A'
B'
C'
D
A
B
C
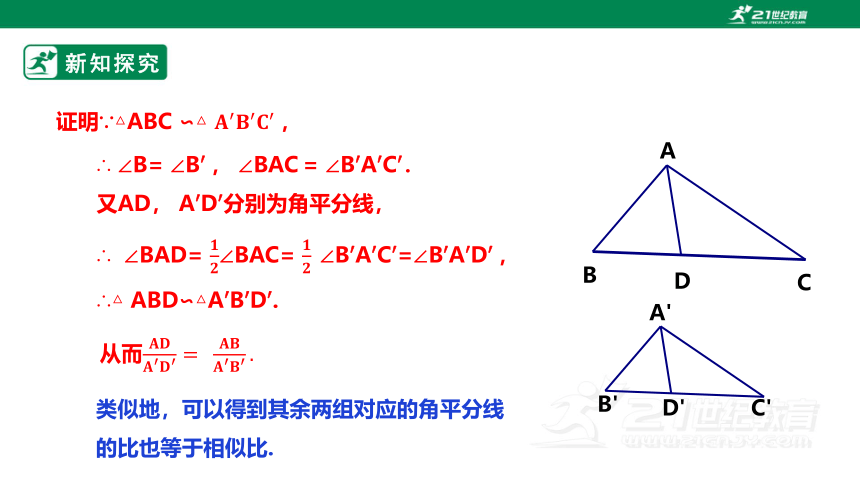
证明∵△ABC ∽△ ,
∴ ∠B= ∠B, ∠BAC = ∠BAC.
又AD, AD分别为角平分线,
∴△ ABD∽△ABD.
从而
∴ ∠BAD= ∠BAC= ∠BAC=∠BAD,
类似地,可以得到其余两组对应的角平分线的比也等于相似比.
新知探究
若△△, AD和A'D'分别是△ABC和△A'B'C'的中线,
那么 成立吗?
D
A
B
D'
A'
B'
C'
C
新知探究
D'
A'
B'
C'
D
A
B
C
证明∵△ABC ∽△ ,
又AD, AD分别为中线,
∴△ ABD∽△ABD.
从而
∴BD= BC, BD= BC,
类似地,可以得到其余两组对应边上的中线的比也等于相似比.
∴
∴
新知探究
结论
由此我们可以得到:
相似三角形对应高的比等于相似比.
类似地,可以证明:
相似三角形对应中线、角平分线的比也等于相似比.
一般地,我们有:
相似三角形对应线段的比等于相似比.
新知探究
例1、如图:△A’B’C’∽△ABC,相似比为,求这两个三角形的角平分线A’D’与AD的比.
解:∵△A’B’C’ ∽△ABC,
∴∠B’=∠B,∠B’A’C’=∠BAC.
∵A’D’,AD分别是△A’B’C’与△ABC的角平分线,
∴∠B’A’D’=∠B’A’C’,∠BAD=∠BAC.
∴∠B’A’D’=∠BAD
∴∠B’A’D’=∠BAD
∴△A’B’D’∽△ABD
∴
新知探究
例2、已知:如图 ,BD,CE是△ABC的两条中线, P是它们的交点.
求证:.
解:连结DE.
∴△DEP∽ △BCP
∴DE//BC,DE=
∵BD,CE是△ABC的两条中线,
∴∠EDB=∠DBC,∠DEC=∠ECB,
∴
新知探究
A
B
C
E
P
F
P
G
如图,△ABC的两条中线BE、CF交于P点,那么BC边上的中线AG是否也经过P点呢?
新知探究
A
B
C
E
P
F
P
G
★重心的定义:三角形三条中线的交点叫做三角形的重心.
★重心的性质:三角形的重心分每一条中线成1:2的两条线段.
课堂练习
1.已知△ABC∽△A'B'C',AD、A'D'分别是对应边BC、B‘C’上的中线,若BC=8cm, B'C'=6cm,AD=4cm,则A'D' 等于( )
A. 16cm B. 12 cm C. 3 cm D. 6 cm
2.两个相似三角形对应高的比为3∶7,它们的对应角平分线的比为( )
A . 7∶3 B. 49∶9 C. 9∶49 D. 3∶7
C
D
课堂练习
3. 如果两个相似三角形的对应高的比为 2 : 3,那么对 应角平分线的比是 ,对应边上的中线的比是 ______ .
4. 已知△ABC ∽ △A'B'C' ,相似比为3 : 4,若 BC 边上的高 AD=12 cm,则 B'C' 边上的高 A'D' =______ .
2 : 3
2 : 3
16 cm
5.已知△ABC∽△A′B′C′,AD和A′D′是它们的对应角平分线,且AD=8cm,A′D′=3cm.则△ABC与△A′B′C′对应高的比为____.
课堂练习
6.如图,△ABC∽△DEF,AG,DH 分别是△ABC和△DEF的角平分线,
BC=6cm,EF=4 cm,AG=4 cm,求DH 的长.
解 : ∵△ABC∽△DEF,
∴ =.
∵ BC=6cm,EF=4cm, AG=4 cm,
∴ =
∴ DH=(cm).
课堂练习
7.已知△ABC∽△DEF,BG、EH分别是△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
解:∵ △ABC∽△DEF,
解得,EH=3.2(cm).
答:EH的长为3.2cm.
A
G
B
C
D
E
F
H
课堂练习
8.如图,△ABC是一块锐角三角形余料,其中BC=15cm,高AD=10cm,现在要把它裁剪成一个矩形材料备用,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,若矩形的一边PN=9cm,求矩形的另一边PQ的长是多少?
课堂练习
解:设AD与PN交于点E.
∵四边形PQMN是矩形,
∴PN∥BC,
∴∠APN=∠B,∠ANP=∠C,
∴△APN∽△ABC,
∴DE=AD-AE=10-6=4(cm),
由题意可知:PQ=DE=4cm.
∴矩形的另一边PQ的长是4cm.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
4.5.1相似三角形的性质及应用
浙教版 九年级上册
教学目标
教学目标:
1.经历相似三角形性质“相似三角形对应高线、对应中线、对应角平分线之比等于相似比.
巩固相似三角形性质,并能熟练运用.
重点:相似三角形的性质及对应线段的性质.
难点:掌握相似三角形性质的应用.
新课导入
A
C
B
A1
C1
B1
问题: ΔABC与ΔA1B1C1相似吗?
新课导入
A
C
B
A1
C1
B1
相似三角形对应角相等、对应边成比例.
ΔABC∽ ΔA1B1C1
新课导入
思考:三角形中,除了角度和边长外,还有哪些几何量?
高、角平分线、中线的长度,周长、面积等
高
角平分线
中线
新知探究
合作探究
如图,△ABC ∽△A′B′C′,相似比为 k,它们对应高、对应中线、对应角平分线的比各是多少?
A
B
C
A'
B'
C'
新知探究
∵△ABC ∽△A′B′C′,
∴∠B=∠B' ,
解:如图,分别作出 △ABC 和
△A' B' C' 的高 AD 和 A' D' .
则∠ADB =∠A' D' B'=90°.
∴△ABD ∽△A' B' D' .
A
B
C
A'
B'
C'
D'
D
∴
如图,△ABC ∽△A′B′C′,相似比为 k,求它们对应高的比.
新知探究
若△△, AD和AD分别是△ABC和△ABC的角平分线,
那么 成立吗?
D'
A'
B'
C'
D
A
B
C
新知探究
D'
A'
B'
C'
D
A
B
C
证明∵△ABC ∽△ ,
∴ ∠B= ∠B, ∠BAC = ∠BAC.
又AD, AD分别为角平分线,
∴△ ABD∽△ABD.
从而
∴ ∠BAD= ∠BAC= ∠BAC=∠BAD,
类似地,可以得到其余两组对应的角平分线的比也等于相似比.
新知探究
若△△, AD和A'D'分别是△ABC和△A'B'C'的中线,
那么 成立吗?
D
A
B
D'
A'
B'
C'
C
新知探究
D'
A'
B'
C'
D
A
B
C
证明∵△ABC ∽△ ,
又AD, AD分别为中线,
∴△ ABD∽△ABD.
从而
∴BD= BC, BD= BC,
类似地,可以得到其余两组对应边上的中线的比也等于相似比.
∴
∴
新知探究
结论
由此我们可以得到:
相似三角形对应高的比等于相似比.
类似地,可以证明:
相似三角形对应中线、角平分线的比也等于相似比.
一般地,我们有:
相似三角形对应线段的比等于相似比.
新知探究
例1、如图:△A’B’C’∽△ABC,相似比为,求这两个三角形的角平分线A’D’与AD的比.
解:∵△A’B’C’ ∽△ABC,
∴∠B’=∠B,∠B’A’C’=∠BAC.
∵A’D’,AD分别是△A’B’C’与△ABC的角平分线,
∴∠B’A’D’=∠B’A’C’,∠BAD=∠BAC.
∴∠B’A’D’=∠BAD
∴∠B’A’D’=∠BAD
∴△A’B’D’∽△ABD
∴
新知探究
例2、已知:如图 ,BD,CE是△ABC的两条中线, P是它们的交点.
求证:.
解:连结DE.
∴△DEP∽ △BCP
∴DE//BC,DE=
∵BD,CE是△ABC的两条中线,
∴∠EDB=∠DBC,∠DEC=∠ECB,
∴
新知探究
A
B
C
E
P
F
P
G
如图,△ABC的两条中线BE、CF交于P点,那么BC边上的中线AG是否也经过P点呢?
新知探究
A
B
C
E
P
F
P
G
★重心的定义:三角形三条中线的交点叫做三角形的重心.
★重心的性质:三角形的重心分每一条中线成1:2的两条线段.
课堂练习
1.已知△ABC∽△A'B'C',AD、A'D'分别是对应边BC、B‘C’上的中线,若BC=8cm, B'C'=6cm,AD=4cm,则A'D' 等于( )
A. 16cm B. 12 cm C. 3 cm D. 6 cm
2.两个相似三角形对应高的比为3∶7,它们的对应角平分线的比为( )
A . 7∶3 B. 49∶9 C. 9∶49 D. 3∶7
C
D
课堂练习
3. 如果两个相似三角形的对应高的比为 2 : 3,那么对 应角平分线的比是 ,对应边上的中线的比是 ______ .
4. 已知△ABC ∽ △A'B'C' ,相似比为3 : 4,若 BC 边上的高 AD=12 cm,则 B'C' 边上的高 A'D' =______ .
2 : 3
2 : 3
16 cm
5.已知△ABC∽△A′B′C′,AD和A′D′是它们的对应角平分线,且AD=8cm,A′D′=3cm.则△ABC与△A′B′C′对应高的比为____.
课堂练习
6.如图,△ABC∽△DEF,AG,DH 分别是△ABC和△DEF的角平分线,
BC=6cm,EF=4 cm,AG=4 cm,求DH 的长.
解 : ∵△ABC∽△DEF,
∴ =.
∵ BC=6cm,EF=4cm, AG=4 cm,
∴ =
∴ DH=(cm).
课堂练习
7.已知△ABC∽△DEF,BG、EH分别是△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
解:∵ △ABC∽△DEF,
解得,EH=3.2(cm).
答:EH的长为3.2cm.
A
G
B
C
D
E
F
H
课堂练习
8.如图,△ABC是一块锐角三角形余料,其中BC=15cm,高AD=10cm,现在要把它裁剪成一个矩形材料备用,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,若矩形的一边PN=9cm,求矩形的另一边PQ的长是多少?
课堂练习
解:设AD与PN交于点E.
∵四边形PQMN是矩形,
∴PN∥BC,
∴∠APN=∠B,∠ANP=∠C,
∴△APN∽△ABC,
∴DE=AD-AE=10-6=4(cm),
由题意可知:PQ=DE=4cm.
∴矩形的另一边PQ的长是4cm.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
