5.4.3一元一次方程的应用 课件(共17张PPT)
文档属性
| 名称 | 5.4.3一元一次方程的应用 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 880.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-10 10:27:04 | ||
图片预览






文档简介
(共17张PPT)
5.4.3一元一次方程的应用
浙教版 七年级上册
教学目标
教学目标:
1.掌握列方程解应用题的一般步骤。
2.掌握诸如行程问题、等积变形、调配问题、利率问题、工程问题这些常见的数量关系,列出方程。
重点:掌握列方程解应用题的一般步骤,及掌握常见的基本数量关系,列出方程.
难点:让学生学会用列表法、图示法分析应用题中的数量关系.
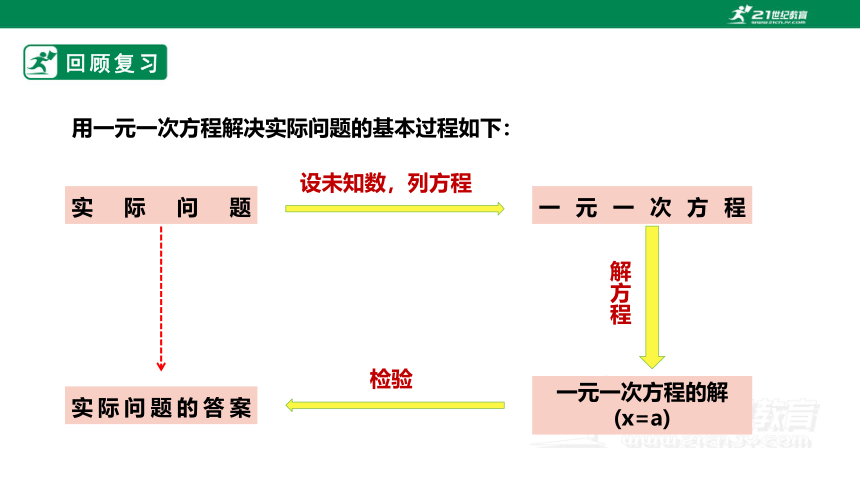
用一元一次方程解决实际问题的基本过程如下:
实际问题
设未知数,列方程
一元一次方程
实际问题的答案
解方程
一元一次方程的解 (x=a)
检验
回顾复习
新知探究
例5 学校组织植树活动,已知在甲处植树的有23人,在乙处植树的有17人.现调20人去支援,使在甲处植树的人数是乙处植树人数的2倍,问应调往甲、乙两处各多少人?
甲处 乙处
原有人数
增加人数
增加后人数
17+20-x
23+x
20-x
x
23
17
分析 设应调往甲处x人,题目中所涉及的有关数量及其关系可以用下表表示:
甲处增加后人数=2×乙处增加后人数
新知探究
解:设应调往甲处 x 人,根据题意,得
23+ x =2(17+20 - x ).
解这个方程,得 x =17.
∴ 20-x =3
答:应调往甲处17人,乙处3人.
想一想:如果调往乙处的人数为x,方程应怎样列
新知探究
解:设调往乙队有x人,则调往甲队有(20-x)
根据题意得:2(17+x)=23+(20-x)
解得:x=3
则20-x=20-3=17(人)
答:应调往甲处17人,乙处3人.
新知探究
例6、甲每天生产某种零件80个,甲生产3天后,乙也加入生产同一种零件,再经过5天,两人共生产这种零件940个,问乙每天生产这种零件多少个?
头3天甲生产
零件的个数
甲乙后5天生产零件的总个数
甲后5天生
产的个数
乙后5天生
产的个数
940个
图示
前3天甲生产 后5天甲生产 后5天乙生产
零件的个数 + 零件的个数 + 零件的个数 =940
新知探究
解 设乙每天生产零件 X个.根据题意,得
3×80+5×80+5x=940
解这个方程,得 X=60.
答:乙每天生产零件60个.
画示意图也是分析数量关系的常用方法.
根据这一相等关系,设乙每天生产零件x个,就可以列出方程.
新知探究
对于数量关系较为复杂的应用题,
我们经常采用的方法是:先画出示意图(图示法)使题目中的条件和结论变得直观明显;然后建立方程。
1. 某项工作甲单独做4天完成,乙单独做6天完成,若甲先干1天,然后甲、乙合作完成此项工程,若设甲一共做了x天,则所列方程为( )
B.
C. D.
C
课堂练习
2.若要求二人在8天内完成任务,乙先加工几天后,甲加入合作加工,恰好能如期完成任务?
效率 时间 工作量
甲
乙
8
x
列表分析
课堂练习
解:设甲加工x天,两人如期完成任务,则在甲加入之前,乙先工作了(8-x)天.
依题意,得
解得x=4,则8-x=4.
答:乙需加工4天后,甲加入合作加工才可正好按期完成任务.
课堂练习
3. 某班学生分两组参加某项活动,甲组有26人,乙组有32人,后来由于活动需要,从甲组抽调了部分学生去乙组,结果乙组的人数比甲组人数的2倍还多1人.从甲组抽调了多少名学生去乙组?
解:设从甲组抽调了x名学生去乙组.
根据题意,得2(26-x)+1=32+x,解得x=7.
答:从甲组抽调了7名学生去乙组.
课堂练习
4. 一个道路工程,甲队单独施工9天完成,乙队单独做24天完成.现在甲乙两队共同施工3天,因甲另有任务,剩下的工程由乙队完成,问乙队还需几天才能完成?
解:设乙队还需x天才能完成,由题意得:
解得 x = 13.
答:乙队还需13天才能完成.
课堂练习
课堂小结
一元一次方程的应用
劳动力调配问题中的相等关系
调配前量的关系
调配后量的关系
工程问题
基本公式:工作量=工作效率×工作时间
相等关系:全部工作量=各部分工作量之和
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
5.4.3一元一次方程的应用
浙教版 七年级上册
教学目标
教学目标:
1.掌握列方程解应用题的一般步骤。
2.掌握诸如行程问题、等积变形、调配问题、利率问题、工程问题这些常见的数量关系,列出方程。
重点:掌握列方程解应用题的一般步骤,及掌握常见的基本数量关系,列出方程.
难点:让学生学会用列表法、图示法分析应用题中的数量关系.
用一元一次方程解决实际问题的基本过程如下:
实际问题
设未知数,列方程
一元一次方程
实际问题的答案
解方程
一元一次方程的解 (x=a)
检验
回顾复习
新知探究
例5 学校组织植树活动,已知在甲处植树的有23人,在乙处植树的有17人.现调20人去支援,使在甲处植树的人数是乙处植树人数的2倍,问应调往甲、乙两处各多少人?
甲处 乙处
原有人数
增加人数
增加后人数
17+20-x
23+x
20-x
x
23
17
分析 设应调往甲处x人,题目中所涉及的有关数量及其关系可以用下表表示:
甲处增加后人数=2×乙处增加后人数
新知探究
解:设应调往甲处 x 人,根据题意,得
23+ x =2(17+20 - x ).
解这个方程,得 x =17.
∴ 20-x =3
答:应调往甲处17人,乙处3人.
想一想:如果调往乙处的人数为x,方程应怎样列
新知探究
解:设调往乙队有x人,则调往甲队有(20-x)
根据题意得:2(17+x)=23+(20-x)
解得:x=3
则20-x=20-3=17(人)
答:应调往甲处17人,乙处3人.
新知探究
例6、甲每天生产某种零件80个,甲生产3天后,乙也加入生产同一种零件,再经过5天,两人共生产这种零件940个,问乙每天生产这种零件多少个?
头3天甲生产
零件的个数
甲乙后5天生产零件的总个数
甲后5天生
产的个数
乙后5天生
产的个数
940个
图示
前3天甲生产 后5天甲生产 后5天乙生产
零件的个数 + 零件的个数 + 零件的个数 =940
新知探究
解 设乙每天生产零件 X个.根据题意,得
3×80+5×80+5x=940
解这个方程,得 X=60.
答:乙每天生产零件60个.
画示意图也是分析数量关系的常用方法.
根据这一相等关系,设乙每天生产零件x个,就可以列出方程.
新知探究
对于数量关系较为复杂的应用题,
我们经常采用的方法是:先画出示意图(图示法)使题目中的条件和结论变得直观明显;然后建立方程。
1. 某项工作甲单独做4天完成,乙单独做6天完成,若甲先干1天,然后甲、乙合作完成此项工程,若设甲一共做了x天,则所列方程为( )
B.
C. D.
C
课堂练习
2.若要求二人在8天内完成任务,乙先加工几天后,甲加入合作加工,恰好能如期完成任务?
效率 时间 工作量
甲
乙
8
x
列表分析
课堂练习
解:设甲加工x天,两人如期完成任务,则在甲加入之前,乙先工作了(8-x)天.
依题意,得
解得x=4,则8-x=4.
答:乙需加工4天后,甲加入合作加工才可正好按期完成任务.
课堂练习
3. 某班学生分两组参加某项活动,甲组有26人,乙组有32人,后来由于活动需要,从甲组抽调了部分学生去乙组,结果乙组的人数比甲组人数的2倍还多1人.从甲组抽调了多少名学生去乙组?
解:设从甲组抽调了x名学生去乙组.
根据题意,得2(26-x)+1=32+x,解得x=7.
答:从甲组抽调了7名学生去乙组.
课堂练习
4. 一个道路工程,甲队单独施工9天完成,乙队单独做24天完成.现在甲乙两队共同施工3天,因甲另有任务,剩下的工程由乙队完成,问乙队还需几天才能完成?
解:设乙队还需x天才能完成,由题意得:
解得 x = 13.
答:乙队还需13天才能完成.
课堂练习
课堂小结
一元一次方程的应用
劳动力调配问题中的相等关系
调配前量的关系
调配后量的关系
工程问题
基本公式:工作量=工作效率×工作时间
相等关系:全部工作量=各部分工作量之和
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
