5.5平行四边形的判定(1)[下学期]

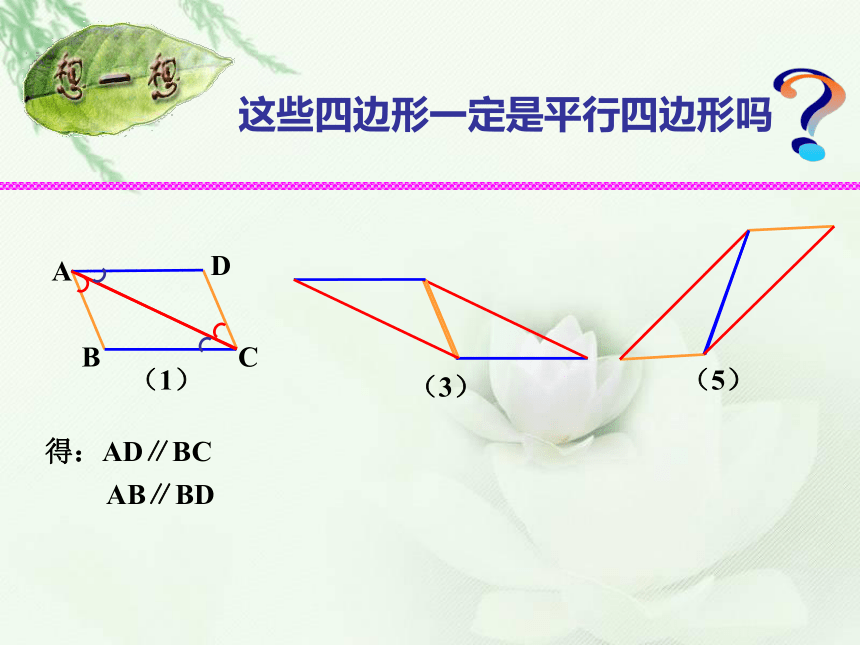
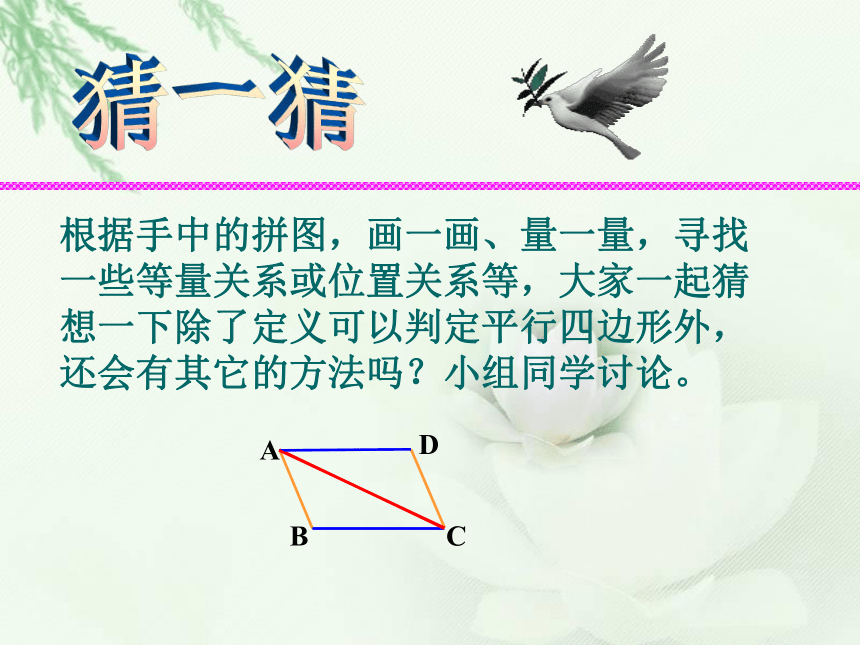
课件15张PPT。5.5 平行四边形 的判定（1） 剪二个全等的三角形纸片，在平面上把它们拼在一起，使一组对应边互相重合。所得的图形一定是平行四边形吗?根据平行四边形的定义可以判断下列哪些四边形是平行四边形?①②④③⑤⑥还有其它判定方法吗?得：AD∥BC AB∥BD 这些四边形一定是平行四边形吗？猜一猜根据手中的拼图，画一画、量一量，寻找一些等量关系或位置关系等，大家一起猜想一下除了定义可以判定平行四边形外，还会有其它的方法吗？小组同学讨论。一般的，我们有下面判定一个四边形是平行四边形的定理：定理1 一组对边平行并且相等的四边形 是平行四边形。定理2 两组对边分别相等的四边形是平行四边形。证明定理1练习：证明定理2“一组对边平行且相等的四边形是平行四边形”这个命题是否真命题？ 求证：四边形ABCD是平行四边形。 证明：连接AC ∵AD∥BC ∴∠DAC=∠ACB又∵AD=BC，AC=AC， ∴ΔABC≌ΔCDA∴∠BAC=∠ACD∴AB∥CD ∴该命题是真命题 （根据什么？） ∴四边形ABCD是平行四边形 （平行四边形的定义）(1)一组对边平行，另一组对边相等的四边形是平行四边形。合作学习：下列命题是真命题还是假命题？如果是假命题,请给出反例。如果是真命题,请给出证明。假命题例1已知：如图，在 中，E，F分别是AB,CD的中点。
求证：四边形ABCD是平行四边形。EBFCDA例2 已知∠ABC，使以AB，BC为两边的平行四边ABCD。你有几种不同的画法（不写画法，保留画图痕迹）1.已知：如图，E,F分别是 的边AD,BC的中点。
求证：BE=DF.D证明：∵四边形ABCD是平行四边形，∴AB∥CD (平行四边形的定义)AD=BC(平行四边形的对边分别相等)，∵E,F分别是AD,BC的中点，∴四边形EBFD是平行四边形（一组对边 平行并且相等的四边形是平行四边形）。课内练习∴BE=DF(平行四边形的对边分别相等)。课内练习2。已知：如图，CD是线段AB经平移所得的像，连结AD,BC.
求证：四边形ABCD是平行四边形。DCBA证明：∵CD是AB经平移所得的像，∴四边形ABCD是平行四边形（一组对边平行并且相等的四边形是平行四边形）。课内练习3.已知：如图，AD⊥AC,BC⊥AC,且AB=CD.
求证：AB∥CD.DCAB证明：∵AD⊥AC, BC⊥AC,∴AD∥BC, ∠BCA=∠DAC=90O,又∵AB=CD, AC=CA,∴Rt⊿ACB≌Rt⊿CAD.∴四边形ABCD是平行四边形（一组对边平行且相等的四边形是平行四边形）。∴AB∥CD(平行四边形的定义)。巩固练习已知：如图 4－24（a），在□ABCD中，E，F分别是边AD，BC的中点．求证：EB=DF． FEDCABGH（1）连接AF、EC分别交BE、DF于点G、点H，
你能得出什么结论？ 小组同学讨论。拓展练习（2）连接GH，你又能 得出什么结论？作业：
作业本，课本 再见