5.5平行四边形的判定(1)[下学期]
文档属性
| 名称 | 5.5平行四边形的判定(1)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 685.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-10 10:41:00 | ||
图片预览





文档简介
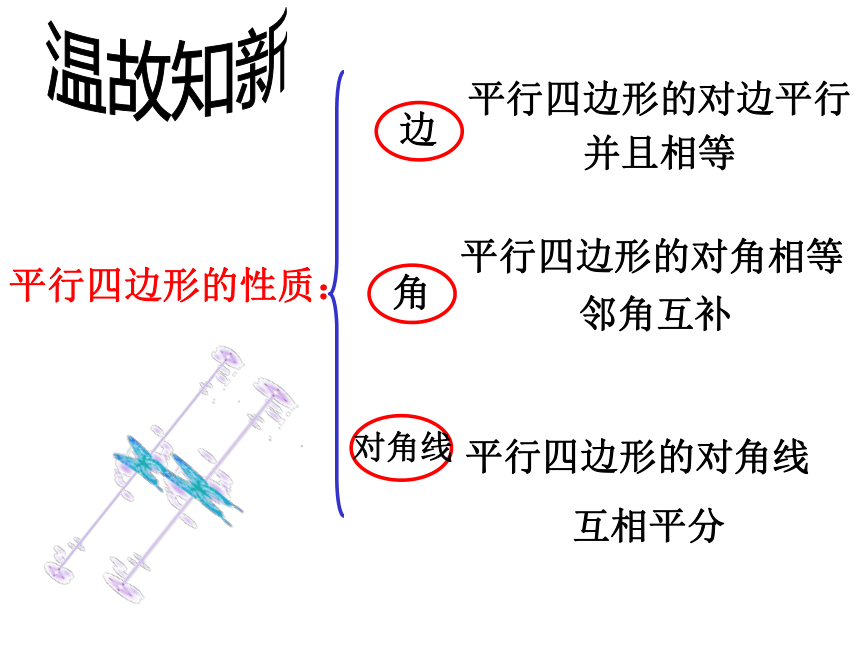
课件20张PPT。平行四边形的判别 1平阳昆二中陈春莲平行四边形的对边平行并且相等平行四边形的对角相等邻角互补 平行四边形的对角线
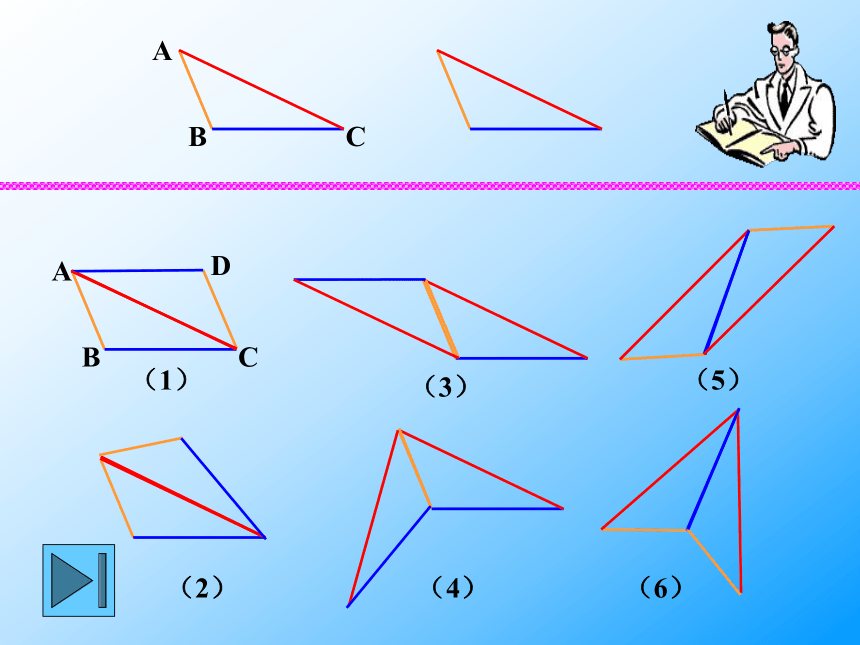
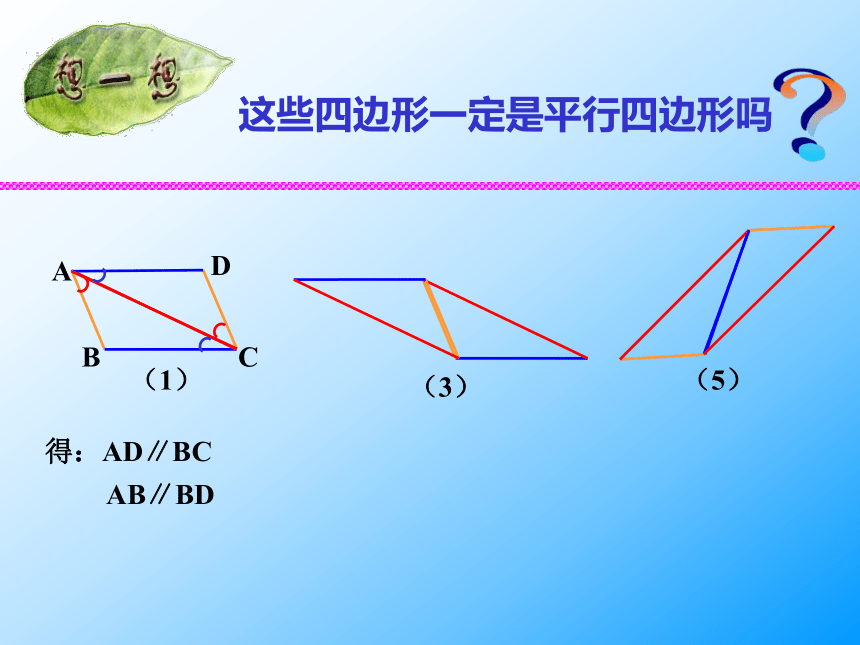
互相平分 温故知新平行四边形的性质: 我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢?ACB得:AD∥BC AB∥BD 这些四边形一定是平行四边形吗?定义:
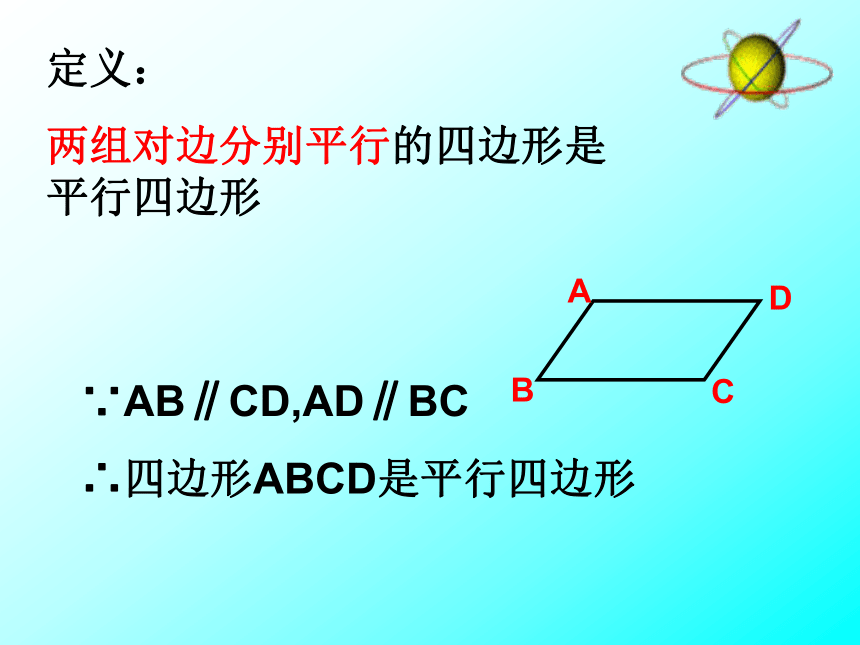
两组对边分别平行的四边形是平行四边形∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形猜一猜根据手中的拼图,画一画、量一量,寻找一些等量关系或位置关系等,大家一起猜想一下除了定义可以判定平行四边形外,还会有其它的方法吗?小组同学讨论。眼见不一定为实!“一组对边平行且相等的四边形是平行四边形”这个命题是否真命题? 求证:四边形ABCD是平行四边形。 证明:连接AC ∵AD∥BC ∴∠DAC=∠ACB又∵AD=BC,AC=AC, ∴ΔABC≌ΔCDA∴∠BAC=∠ACD∴AB∥CD ∴该命题是真命题 (根据什么?) ∴四边形ABCD是平行四边形 (平行四边形的定义)已知:在四边形ABCD中, AD BC。定理1:
一组对边平行且相等的四边
形是平行四边形请同学们证明另外两个命题的真假?
两组对边分别相等的四边形是平行四边形
一组对边平行,另一组对边相等的四边形是平行四边形定理1:
一组对边平行且相等的四边
形是平行四边形定理2:
两组对边分别相等的四边形
是平行四边形。 1、在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠CD试一试:例1 :已知:如图,在□ABCD中,E、F分别
是AB,CD的中点。
求证:EF∥AD∥BC。 AFEDCB课内练习:2、已知:平行四边形ABCD中,E,
F分别是边AD,BC的中点(如图)求证:EB=DF2、已知:平行四边形ABCD中,E,
F分别是边AD,BC的中点(如图)
求证:EB=DF2、已知:平行四边形ABCD中,E,F分别是边AD,BC的中点(如图) 求证:EB=DF 证明:∵四边形ABCD 是平行四边形 ∴AD BC ∵ED=1/2AD BF=1/2BC ∴ED BF ∴四边形EBFD是平行四边形(一组对边平行且相等的四边形是平行四边形)∴EB=DF 延伸提高已知:如图 在□ABCD中,E,F分别是边AD,BC的中点. FEDCABGH(1)连接AF、EC分别交BE、DF于点G、点H,你能得出什么结论? 小组同学讨论。(2)连接GH,你又能 得出什么结论?大显身手证明: 四边形ABCD是平行四边形AD ∥ BC且AD =BCEAD= FCBAE=CF
EAD= FCB
AD=BCAED ≌ CFB(SAS)DE=BF四边形BFDE是平行四边形在 AED和 CFB中同理可证:BE=DF作业题:2、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形我的收获
我的疑惑小结:平行四边形的三个判定方法:
从边看: 两组对边分别平行 两组对边分别相等 一组对边平行且相等 的四边形是平行四边形 再见
互相平分 温故知新平行四边形的性质: 我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢?ACB得:AD∥BC AB∥BD 这些四边形一定是平行四边形吗?定义:
两组对边分别平行的四边形是平行四边形∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形猜一猜根据手中的拼图,画一画、量一量,寻找一些等量关系或位置关系等,大家一起猜想一下除了定义可以判定平行四边形外,还会有其它的方法吗?小组同学讨论。眼见不一定为实!“一组对边平行且相等的四边形是平行四边形”这个命题是否真命题? 求证:四边形ABCD是平行四边形。 证明:连接AC ∵AD∥BC ∴∠DAC=∠ACB又∵AD=BC,AC=AC, ∴ΔABC≌ΔCDA∴∠BAC=∠ACD∴AB∥CD ∴该命题是真命题 (根据什么?) ∴四边形ABCD是平行四边形 (平行四边形的定义)已知:在四边形ABCD中, AD BC。定理1:
一组对边平行且相等的四边
形是平行四边形请同学们证明另外两个命题的真假?
两组对边分别相等的四边形是平行四边形
一组对边平行,另一组对边相等的四边形是平行四边形定理1:
一组对边平行且相等的四边
形是平行四边形定理2:
两组对边分别相等的四边形
是平行四边形。 1、在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠CD试一试:例1 :已知:如图,在□ABCD中,E、F分别
是AB,CD的中点。
求证:EF∥AD∥BC。 AFEDCB课内练习:2、已知:平行四边形ABCD中,E,
F分别是边AD,BC的中点(如图)求证:EB=DF2、已知:平行四边形ABCD中,E,
F分别是边AD,BC的中点(如图)
求证:EB=DF2、已知:平行四边形ABCD中,E,F分别是边AD,BC的中点(如图) 求证:EB=DF 证明:∵四边形ABCD 是平行四边形 ∴AD BC ∵ED=1/2AD BF=1/2BC ∴ED BF ∴四边形EBFD是平行四边形(一组对边平行且相等的四边形是平行四边形)∴EB=DF 延伸提高已知:如图 在□ABCD中,E,F分别是边AD,BC的中点. FEDCABGH(1)连接AF、EC分别交BE、DF于点G、点H,你能得出什么结论? 小组同学讨论。(2)连接GH,你又能 得出什么结论?大显身手证明: 四边形ABCD是平行四边形AD ∥ BC且AD =BCEAD= FCBAE=CF
EAD= FCB
AD=BCAED ≌ CFB(SAS)DE=BF四边形BFDE是平行四边形在 AED和 CFB中同理可证:BE=DF作业题:2、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形我的收获
我的疑惑小结:平行四边形的三个判定方法:
从边看: 两组对边分别平行 两组对边分别相等 一组对边平行且相等 的四边形是平行四边形 再见
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
