5.1多边形（3）[下学期]

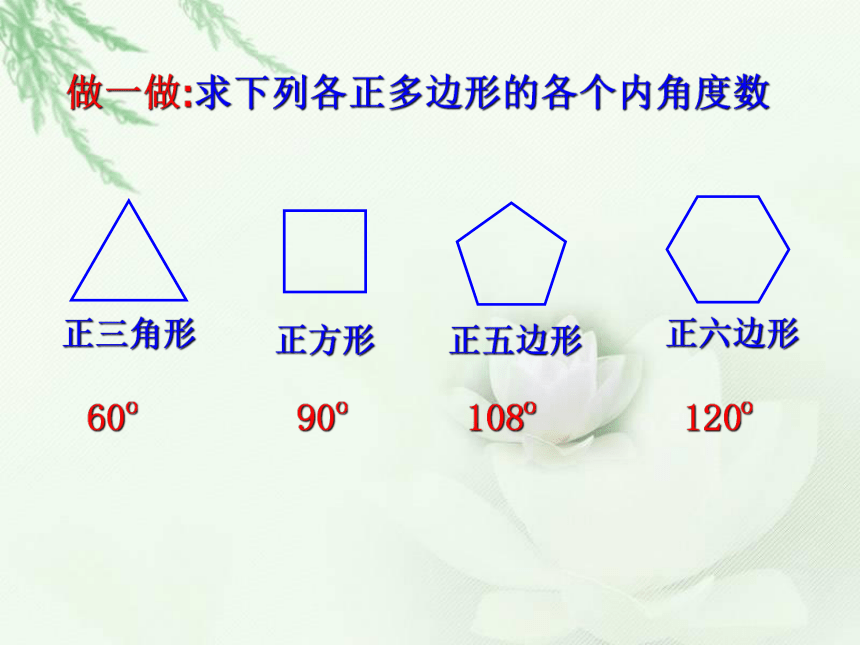
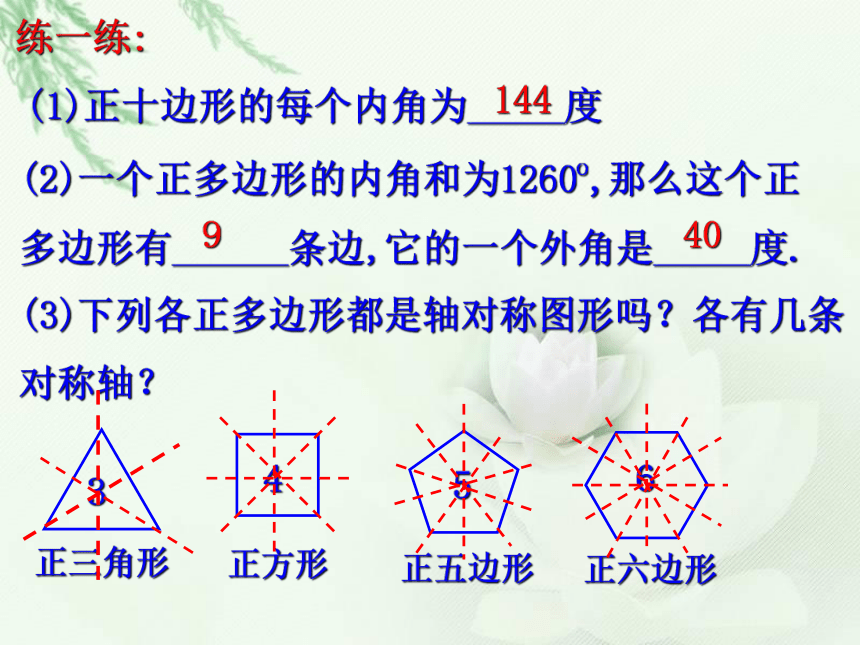
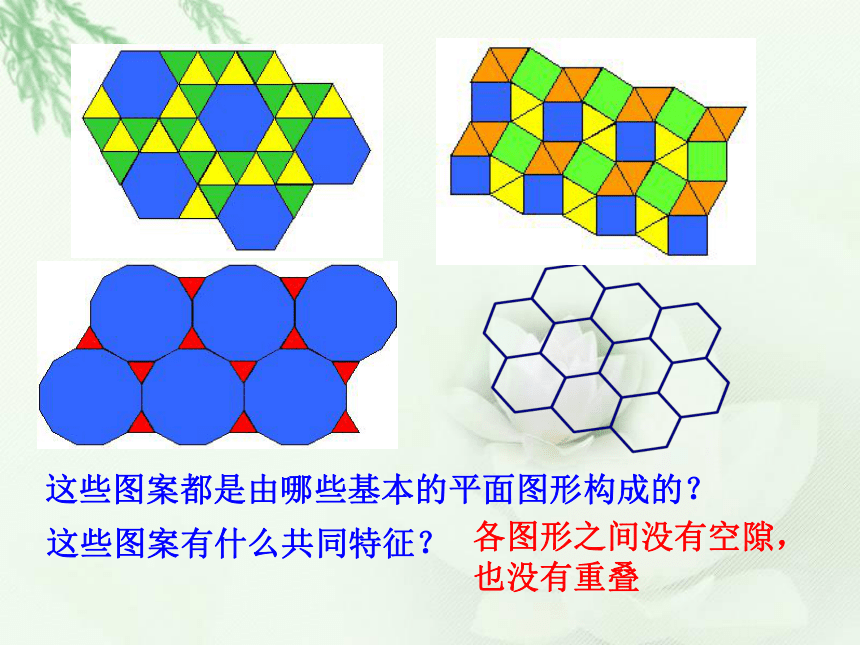
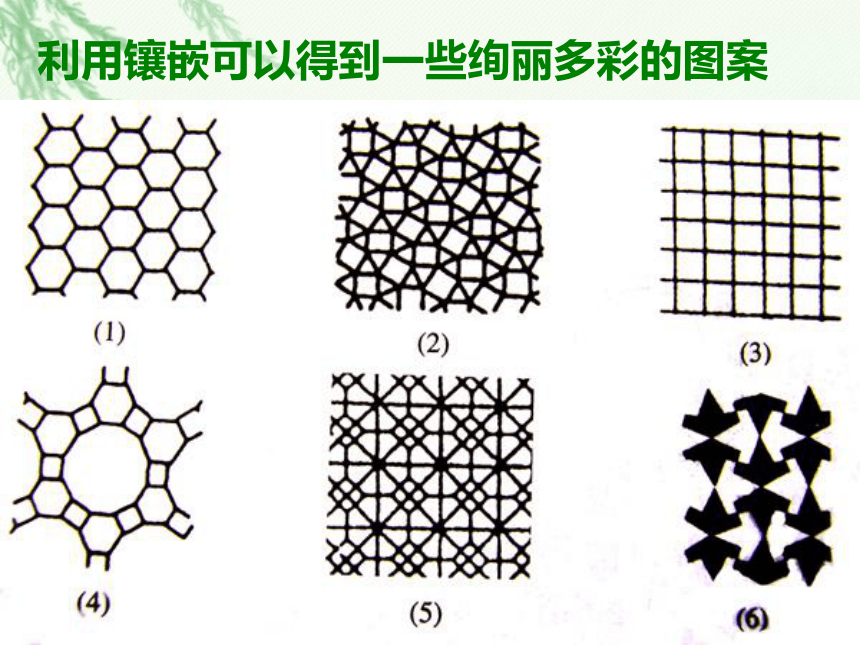
课件31张PPT。5.1多边形(3)正三角形正方形正六边形这些图形中的边与角分别有什么共同的特征？正五边形正多边形:各边相等、各内角也相等的多边形.正多边形:各边相等、各内角也相等的多边形.思考:(1)三边都相等的三角形就是正三角形吗?(2)四边都相等的四边形就是正方形吗?(3)四个角都相等的四边形就是正方形吗?做一做:求下列各正多边形的各个内角度数60o90o108o120o练一练:(1)正十边形的每个内角为_____度144(2)一个正多边形的内角和为1260o,那么这个正多边形有______条边,它的一个外角是_____度.9403456这些图案都是由哪些基本的平面图形构成的？ 这些图案有什么共同特征？ 各图形之间没有空隙，也没有重叠 用一种或几种多边形进行拼接,彼此之间不留空隙,也不重叠地铺成一片,这叫平面图形的镶嵌利用镶嵌可以得到一些绚丽多彩的图案 下列各正多边形中,哪些多边形能单独镶嵌平面，哪些不能，为什么？做一做 （1）用边长相同的正三角形能否镶嵌？结论：用边长相同的正三角形可以镶嵌（2）用边长相同的正方形能否镶嵌？结论：用边长相同的正方形可以镶嵌啊!拼不了啦,为什么呢?你能说说道理吗?123∠1+∠2+∠3=?（3）用边长相同的正五边形能否镶嵌？（4）用边长相同的正六边形能否镶嵌？结论：用边长相同的正六边形可以镶嵌表格1６０°６能拼好９０°４能拼好１０８°３４不能拼好，有缺口不能拼好，有重叠１２０°３能拼好为什么有的正多边形能进行镶嵌，而有的正多边形不能？用一种正多边形镶嵌需要满足什么条件呢？表格2正三角形、正四边形、正六边形能够镶嵌，正五边形不能镶嵌．结论：用一种正多边形镶嵌，则这个正多边形的内角度数能整除360°．你还能找到能镶嵌的其他正多边形吗？要用正多边形镶嵌成一个平面的关键是看：这种正多边形的一个内角的倍数是否是360°，在正多边形里，正三角形的每个内角都是60°，正四边形的每个内角都是90°，正六边形的每个内角都是120°，这三种多边形的一个内角的倍数都是360°，而其他的正多边形的每个内角的倍数都不是360°，所以说：在正多边形里只有正三角形、正四边形、正六边形可以镶嵌，而其他的正多边形不可镶嵌．问1:如果用一种多边形进行镶嵌时不采用正多边形，而改为任意多边形，有没有这样的多边形？有，请指出，并说明理由．结论：有，分别是三角形、四边形，但三角形、四边形各自应形状、大小完全相同（即全等）．
理由：三角形、四边形的内角和均能整除360° 问2：用两种正多边形能否镶嵌，若能，它们需满足什么条件？延伸拓展动一动运用你们组中的正三角形、正四边形、正五边形、正六边形、正八边形，看哪两种能用来搭配镶嵌成一个平面．（边做边记录）(1) ３个正三角形与２个正四边形 60°×3+90°×2=360°
(2) ２个正三角形与２个正六边形 60°×2+120°×2=360°
(3)4个正三角形与1个正六边形 60°×4+120°×1=360°
(4) １个正四边形与２个正八边形 90°×1+135°×2=360°
……多边形能镶嵌成平面图案需要满足的条件 1.拼接在同一个点的各个角的和恰好等于360°(周角)；2.相邻的多边形有公共边．问4：用三种或多种正多边形能否镶嵌，若能，它们需满足什么条件？延伸拓展问3：单独用同一种平面图形如果不能镶嵌,用两种或者两种以上平面图形能不能镶嵌呢?课堂小结 本节课我们通过活动，探讨，知道任意一个三角形，四边形或正六边形可以镶嵌成一个平面，并且探索出正多边形镶嵌的条件．即：一种正多边形的一个内角的倍数是否是360°
作业: 请同学搜集一些平面镶嵌图案,用硬纸片做出其中的一二个模型.能 例如正五边形和正八边形它们单独用同一种不能镶嵌,但与三角形、四边形就能镶嵌成平面图案.