5.1（３）多边形[下学期]

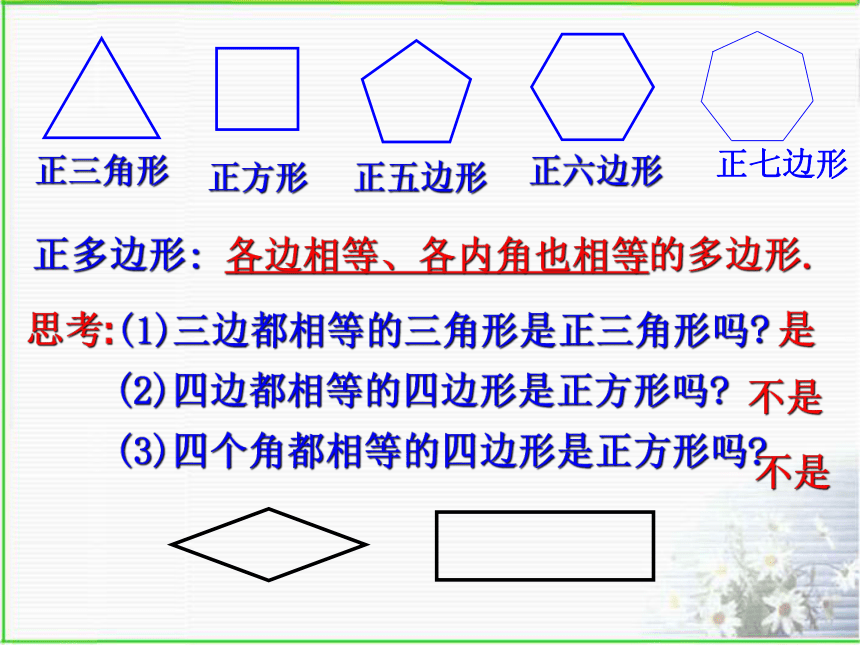
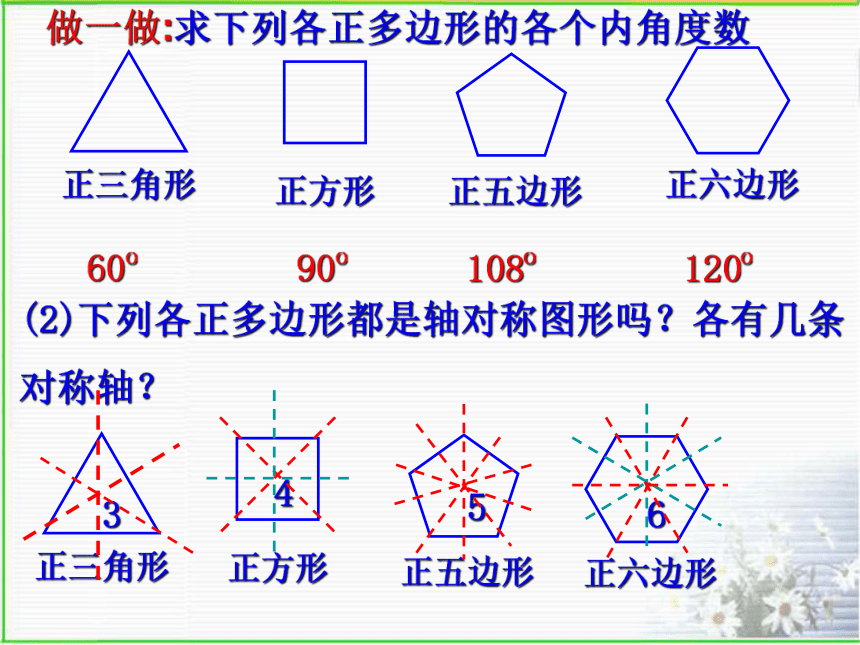
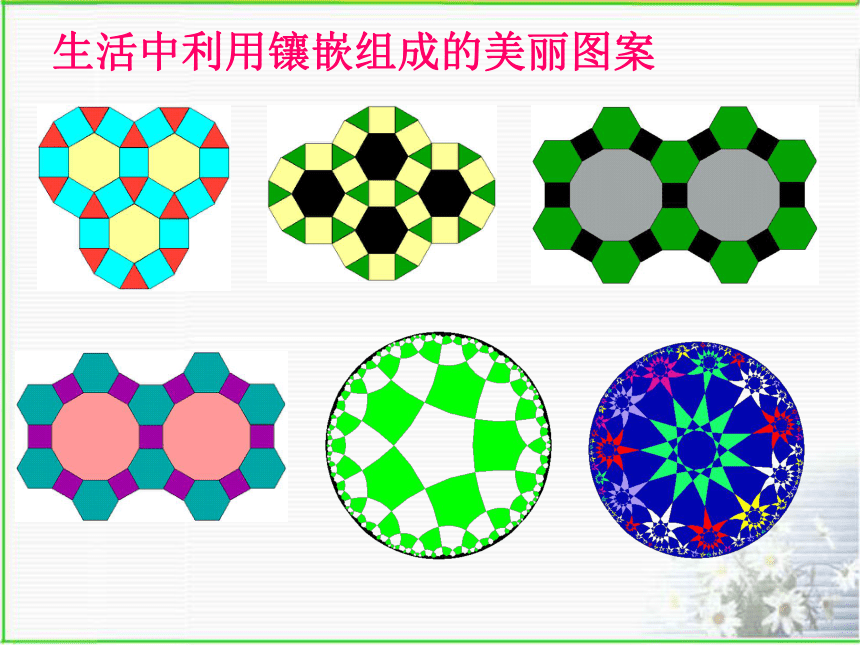
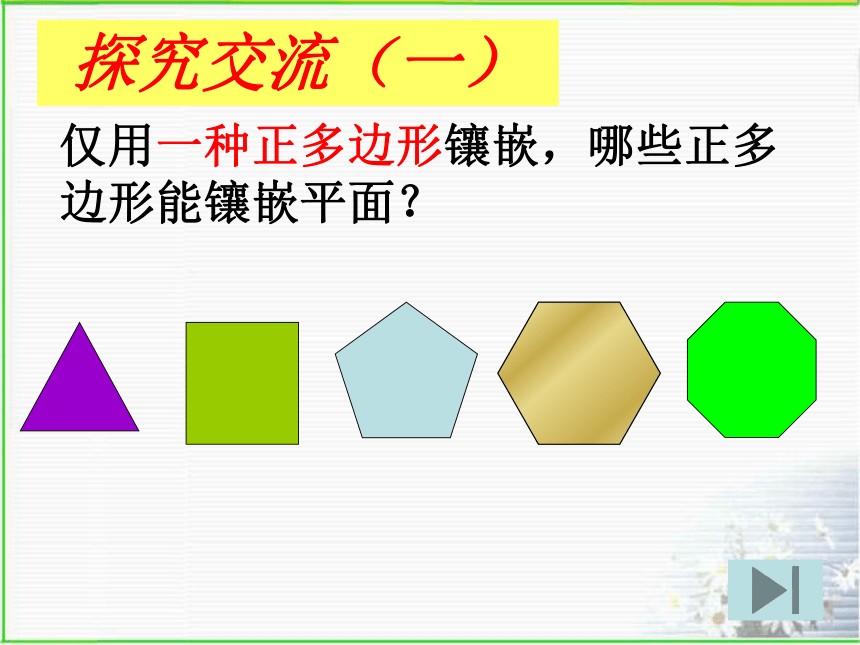
课件44张PPT。考考你：有一张长方形的桌面，它的 四个内角和为360度，现在锯掉它的一个角，剩下残余桌面所有的内角和是多少？分析：5.1多边形(三)人人都参与到数学活动中，相信你能在参与过程中体验到快乐！ 正六边形正五边形正三角形正方形正多边形:各边相等、各内角也相等的多边形.思考:(1)三边都相等的三角形是正三角形吗?(2)四边都相等的四边形是正方形吗?(3)四个角都相等的四边形是正方形吗?是不是不是正七边形345660o90o108o120o做一做:求下列各正多边形的各个内角度数用一种或几种多边形进行拼接,彼此之间不留缝隙,也不重叠地铺成一片,叫做平面图形的镶嵌.（也叫密铺）。生活中利用镶嵌组成的美丽图案仅用一种正多边形镶嵌，哪些正多边形能镶嵌平面？探究交流（一）探究交流一：哪一种正多边形可以单独镶嵌平面？

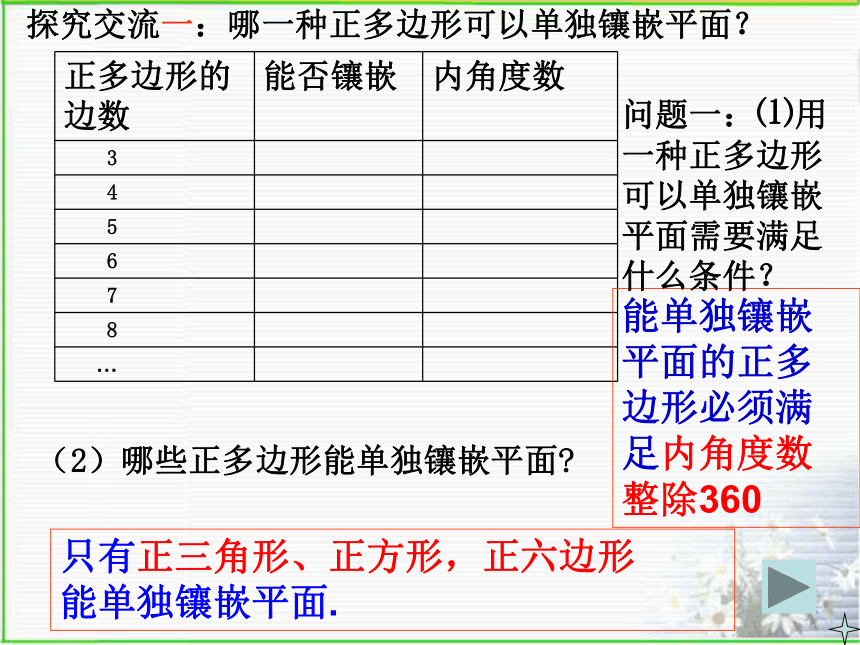
（2）哪些正多边形能单独镶嵌平面? 能单独镶嵌
平面的正多
边形必须满
足内角度数
整除360只有正三角形、正方形，正六边形
能单独镶嵌平面.问题一：⑴用
一种正多边形
可以单独镶嵌
平面需要满足
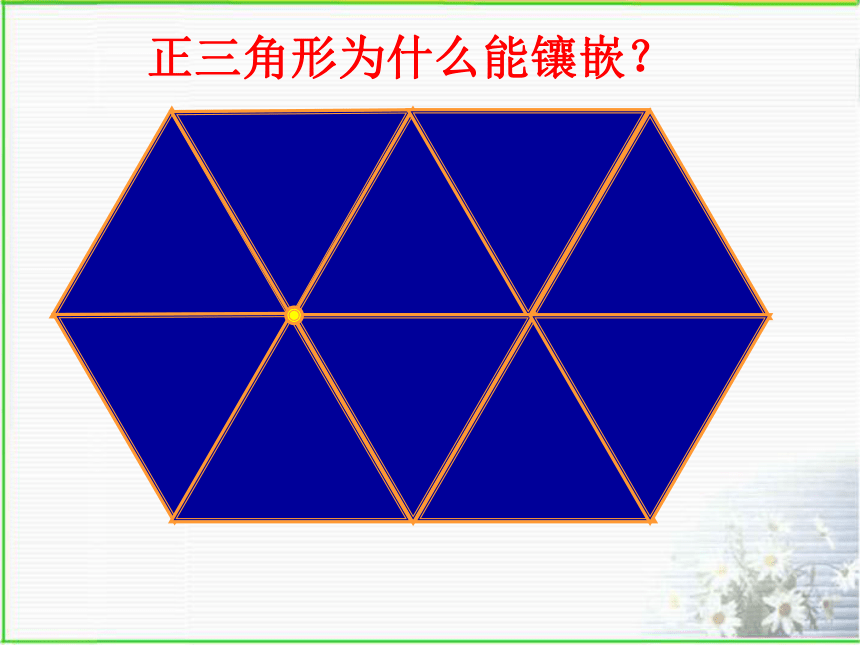
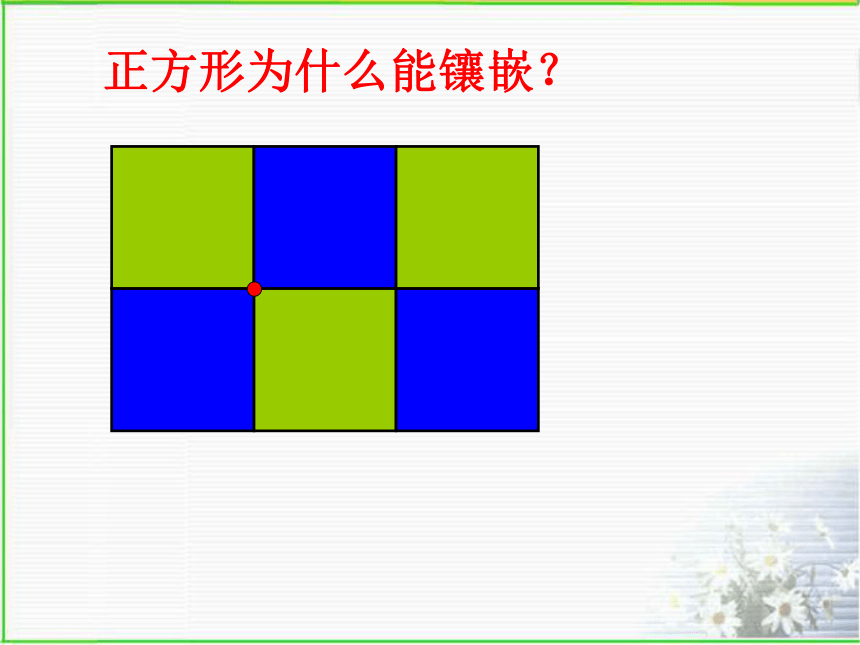
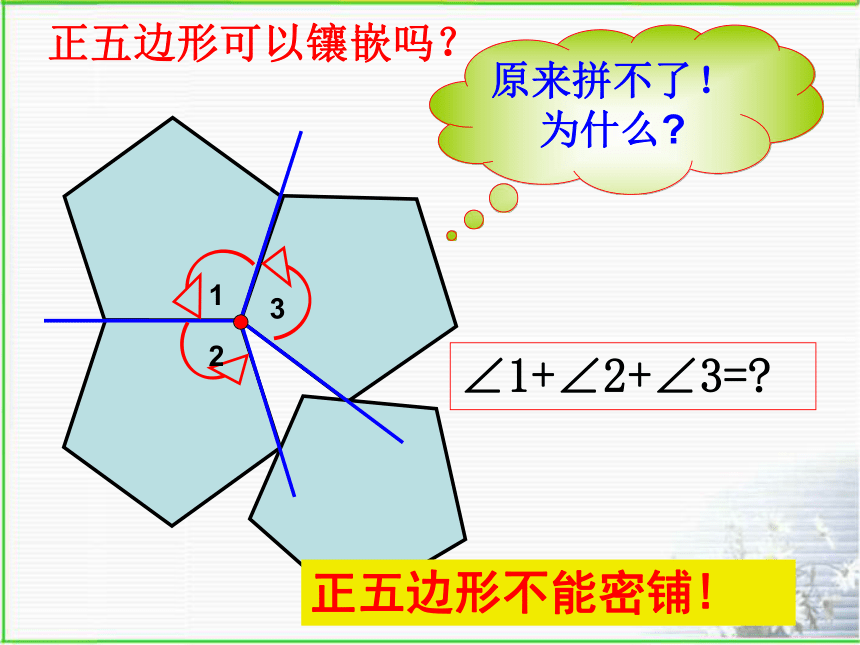
什么条件？正三角形为什么能镶嵌？正方形为什么能镶嵌？123∠1+∠2+∠3=?正五边形可以镶嵌吗？原来拼不了！为什么?正五边形不能密铺!正六边形为什么能镶嵌？正多边形能否镶嵌平面,关键是拼接点处的几个内角和能否构成360°.还有其他的正多边形可以进行镶嵌吗？能能能正三角形正方形正五边形正六边形643不能1.三角形可以作平面镶嵌吗? 若能，三角形将如何镶嵌呢?探究：普通多边形的镶嵌 形状、大小完全相同的任意 三角形可以镶嵌平面吗？如图,四边形ABCD中,因为∠A+∠B+∠C+ ∠D = 360°,所以四边形也可以作平面镶嵌.2.四边形呢?探究：普通多边形的镶嵌 形状、大小完全相同的任意四边形 可以镶嵌平面吗？ 从而发现： 形状、大小完全相同的平面图形 能够镶嵌平面的有： 任意三角形、任意四边形、正六边形.正五边形不能密铺!练习一1. 形状、大小完全相同的任意三角形、四边形 能否单独作镶嵌 ( )
2. 用任意三角形镶嵌平面时,同一顶点处应摆放 ( )个三角形;用任意四边形镶嵌平面时， 同一顶点处应摆放( )个四边形.
3.下面四种正多边形中,用同一种图形不能平面 镶嵌的是( ). 能64C用边长相等的正八边形和正方形能镶嵌平面吗?请说明理由.如果能,画出镶嵌图(只要求画出示意图)例题讲解13501350900探究多种正多边形的组合镶嵌平面探究交流（二）请选择两种能镶嵌平面的正多边形,动手试一试,组成一幅镶嵌图.问题：两种正多边形镶嵌平面需要满足什么条件？结论两种正多边形镶嵌平面需要满足的条件：
（１）共顶点的各个角的和恰好等于
３６００;
（２）这两种正多边形的边长相等．探究：几种多边形的组合镶嵌下列多边形组合，能够密铺平面的是：
（1）正三角形与正方形；
（2）正三角形与正六边形；
（3）正方形与正八边形；
（4）正六边形与正八边形；
（5）正三角形、正方形与正六边形。想一想：哪些正多边形可以组合镶嵌当围绕一点拼在一起的几个正多边形的内角和加在一起恰好组成一个周角时,就能镶嵌一个平面图形;那么哪些正多边形可以进行镶呢？想一想：哪些正多边形可以组合镶嵌两种正多边形的平面镶嵌(1) 正三角形与正方形的平面镶嵌？答：用边长相等的正三角形与正方形能镶嵌平面。因为正三角形的内角为60度，正方形的内角为
90度，根据60°×3+90°×2=360°，所以
3个正三角形和2个正方形能拼成镶嵌图。正三角形和正方形的组合镶嵌注意:同一个组合会有不同的镶嵌效果正三角形和正方形的组合镶嵌(2) 正三角形与正六边形的平面镶嵌？答：用边长相等的正三角形与正六边形能镶嵌平面。因为正三角形的内角为60度，正六边形的内角为
120度，根据60°×4+120°×1=360°及根据
60°×2+120°×2=360°所以4个正三角形和
1个正方形能拼成镶嵌图或2个正三角形和2个正
方形能拼成镶嵌图。
解：设在一个顶点周围有x个正四边形，y个正八边形， 则 x·60°+y·120°=360° 即x+2y=6
这个方程的非负整数解为：
x 1 =4 x 2 =2
y 1 =1 y 2 =2
所以用正四边形和正八边形做平面密铺有两种可能：
(1)在它的一个顶点周围4个正三角形配1个正六边形；
(2)在它的一个顶点周围2个正三角形配2个正六边形；
例:用边长相同的正三角形与正六边形做平面密铺，有几种可能？为什么？关键：得到一个关于边数x，y的方程， 然后求出它的整数解。正三角形与正六边形的组合镶嵌正三角形与正六边形的组合镶嵌解：因为正八边形的内角为135o， 正方形的内角为90o，根据： 135o×2+90o＝360o，所以： 两个正八边形和一个正方形 能拼成一幅镶嵌图.在公共的顶点处各正多边形的内角和等于360°（3) 正方形与正八边形的平面镶嵌？正方形、正八边形的组合镶嵌正三角形、正方形、正六边形的组合镶嵌正三角形、正十二边形的组合镶嵌小结与反思1.镶嵌的要求：无缝隙，不重叠2.多边形能否镶嵌的条件：每个顶点处几个角的和为360°课内练习：如图这幅镶嵌图由几种正多形组成？请说明这几种正多边形能镶嵌平面的数学原理。书本作业题第3题图： 多种正多边形镶嵌平面.欣赏问4：用三种或多种正多边形能否镶嵌，若能，它们需满足什么条件？延伸拓展问3：单独用同一种平面图形如果不能镶嵌,用两种或者两种以上平面图形能不能镶嵌呢? 请选择两种能镶嵌平面的正多边形，动手试一试，组成一幅镶嵌图，然后完成以下工作： ⑴ 说明你选择的两种正多边形能镶嵌平面的数学原理;⑵ 画出你选择的两种正多边形镶嵌平面的图形（示意图）.…探究活动试试看:请你用两种或两种以上的多边形设计镶嵌图案.