5.1 多边形(3)

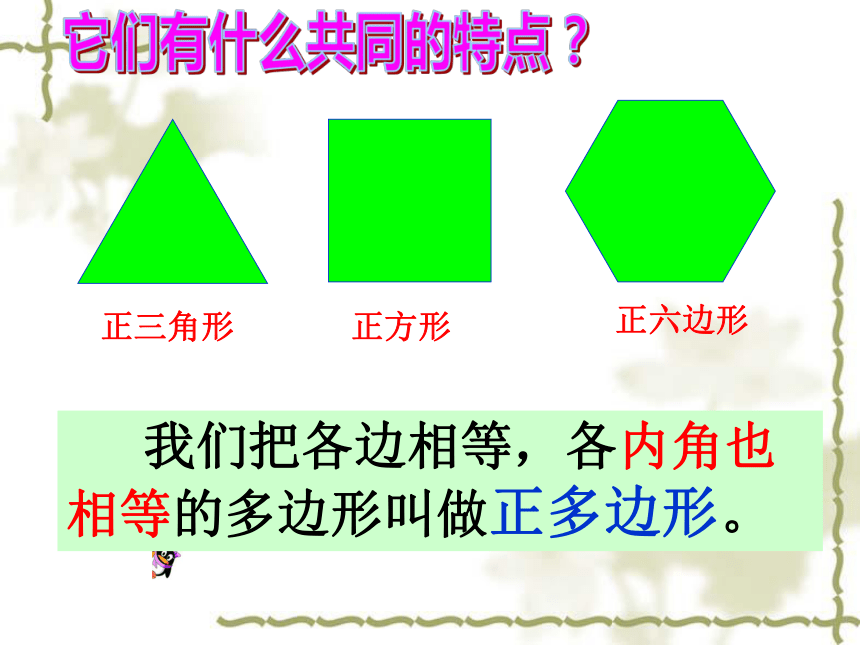
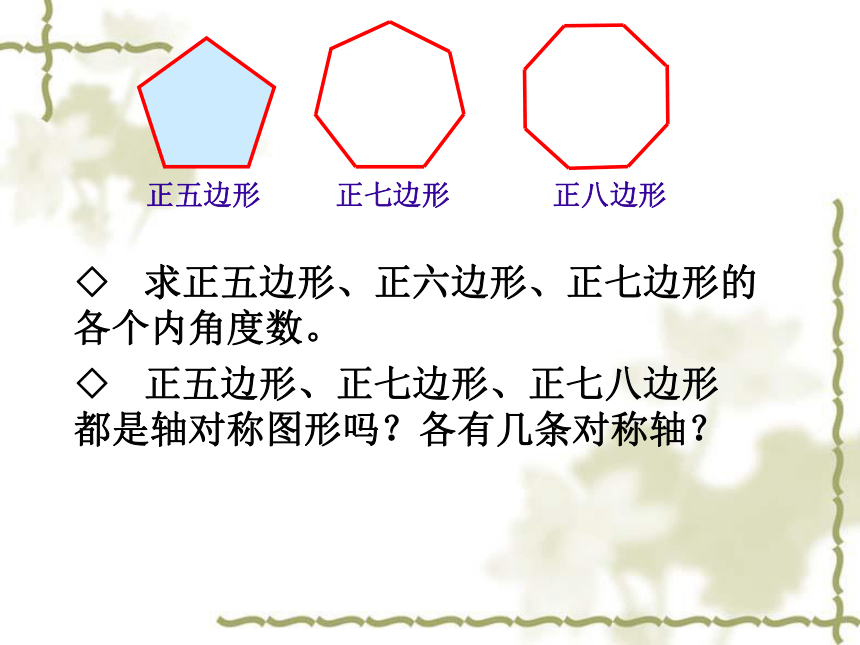
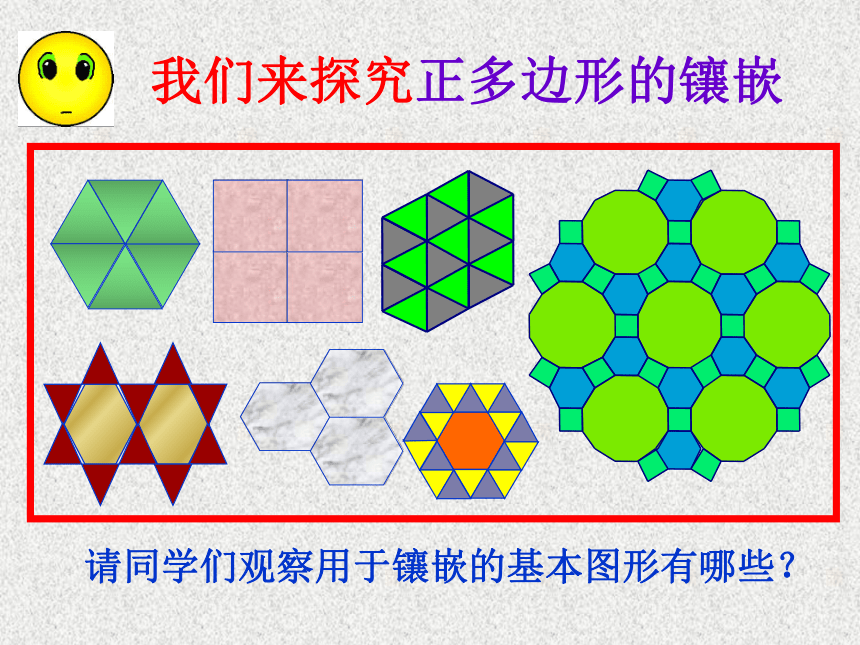
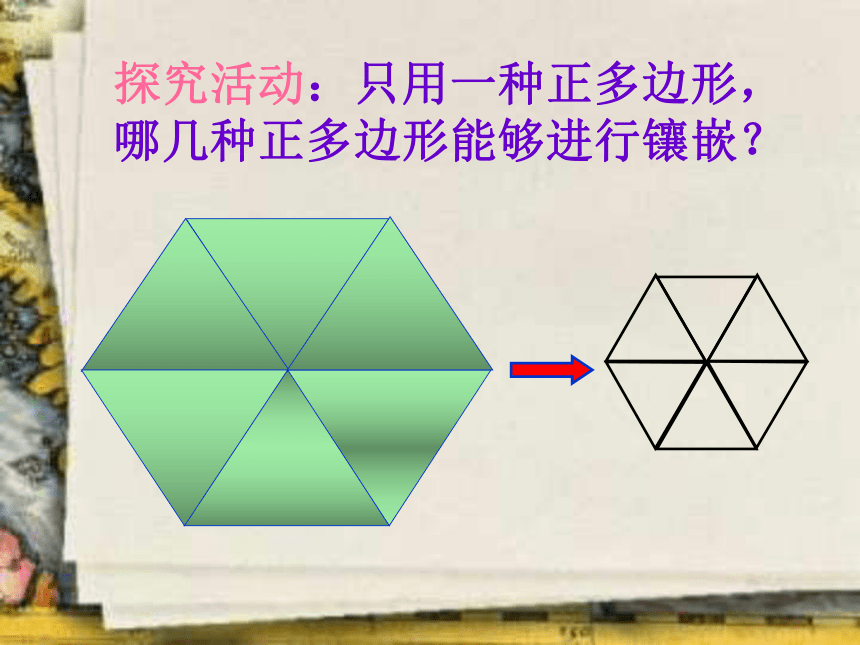
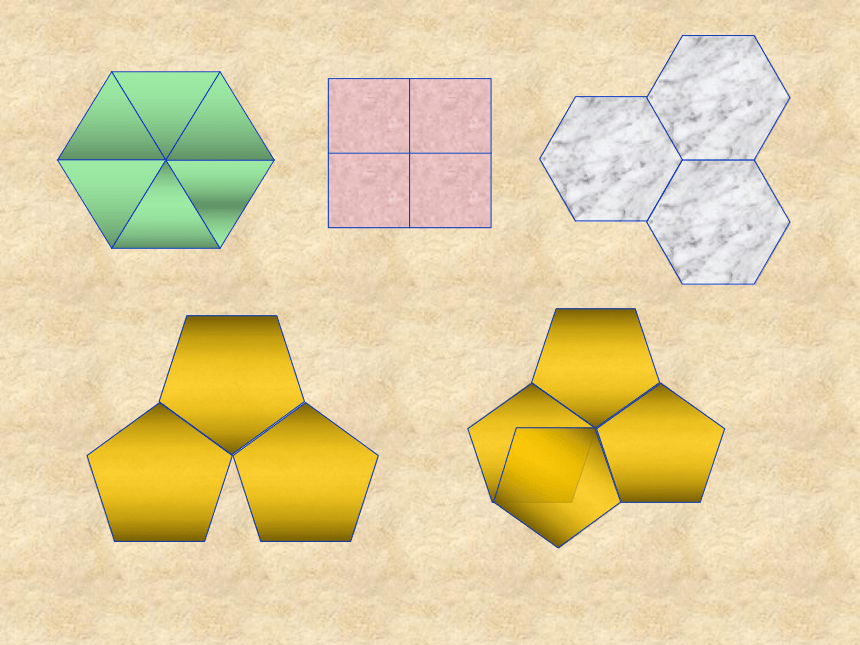
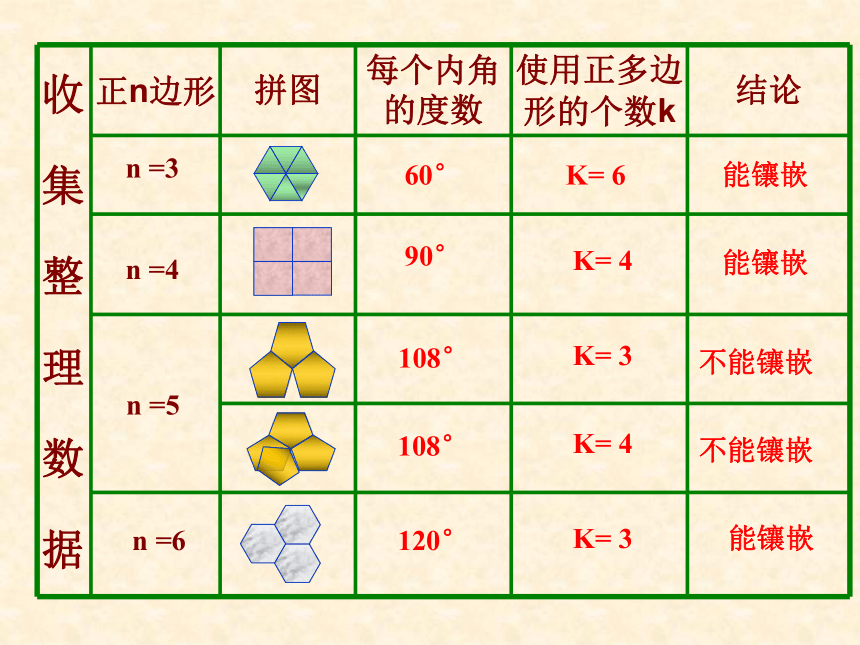
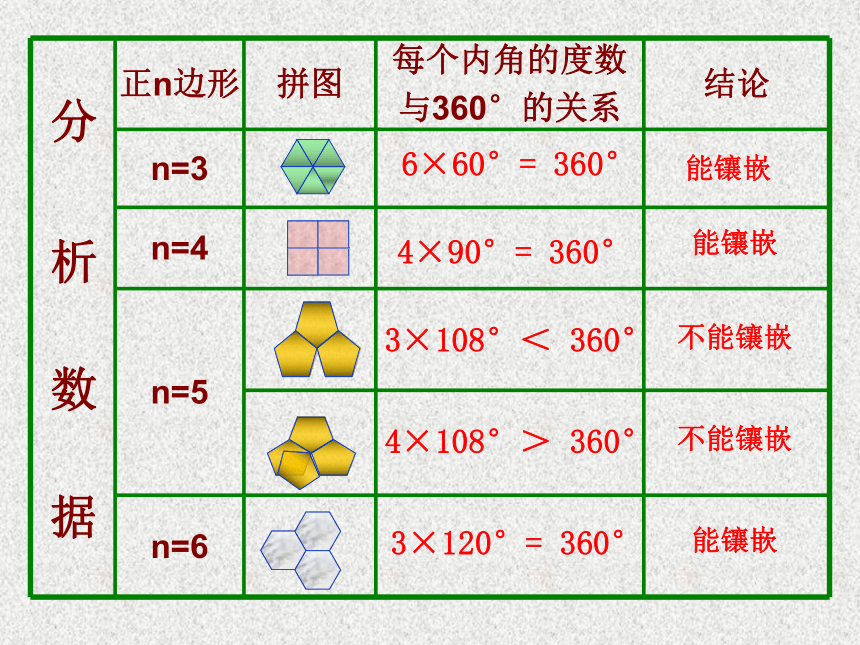
课件30张PPT。 好漂亮的地板!这是怎么铺设的?一点空隙也没有.5.1多边形⑶　　我们把各边相等，各内角也相等的多边形叫做正多边形。它们有什么共同的特点？正三角形正方形正六边形正五边形正七边形正八边形◇ 求正五边形、正六边形、正七边形的各个内角度数。◇ 正五边形、正七边形、正七八边形都是轴对称图形吗？各有几条对称轴？　　由于正多边形有许多优良的性质，匀称美观，常被人们用于图案设计和镶嵌平面. 通过观察上面的图片，你发现它们有哪些共同特征？不重叠完全覆盖 从数学角度看，用一些不重叠摆放的多边形把平面的一部分完全覆盖，通常把这类问题叫做覆盖平面（或平面镶嵌）的问题.　请同学们观察用于镶嵌的基本图形有哪些？我们来探究正多边形的镶嵌探究活动：只用一种正多边形，哪几种正多边形能够进行镶嵌？能镶嵌能镶嵌不能镶嵌不能镶嵌能镶嵌K= 6K= 4K= 3K= 4K= 360°90°108°108°120°n =3n =6n =4n =5能镶嵌不能镶嵌不能镶嵌能镶嵌6×60°= 360°4×90°= 360°4×108°＞ 360°3×120°= 360°3×108°＜ 360°能镶嵌得出结论： 如果一个正多边形可以进行镶嵌，那么内角一定是360°的约数（或360°一定是这个多边形内角的整数倍）！思考：用下列正多边形能镶嵌吗？正7边形？正十边形？正20边形？小试牛刀如果用两种正多边形进行镶嵌需要满足什么条件？小颖家正在为新房子装修，在他的房间里，他想用正三角形和另一种正多边形镶嵌成地板，他有哪些选择？问题3×60°+ 2 ×90°= 360° 3×60+2 ×90°=360°4×60+1 ×120°=360°正三角形正四边形正三角形正六角形得出结论：用两种正多边形镶嵌的规律：拼接在同一个点的各个角的和恰好等于360°（周角）。
正五边形和正十边形能否镶嵌?正四边形和正八边形能否镶嵌?你能说出其中的道理吗牛刀小试得出结论：用两种正多边形镶嵌的规律：拼接在同一个点的各个角的和恰好等于360°（周角）。
两种正多边形的边长相等.
把正三角形、正方形、正六边形三者结合在一起呢？请你试试看.问题探索?正六边形、正方形、正三角形 某足球场需铺设草皮。现有正三角形、正四边形、正六边形、正八边形、四种形状的草皮，假如你是名设计师,你有哪些选择?拓展与应用实验活动：1、用一种任意三角形，怎样进行
镶嵌？2、用一种任意四边形，怎样进行
镶嵌？3、用一种任意梯形，怎样进行
镶嵌？收获与启示什么叫镶嵌
用一种正多边形和两种正多边形镶嵌的规律
数学试验对学习的帮组和启发 请你为小颖同学所选择的正三角形的地板配上另一种正多边形使它们能够镶嵌在小颖的房间里！并写出所有的设计方案！课后思考： Good Good Study ！ Day Day Up ！