5.1多边形（3）[下学期]

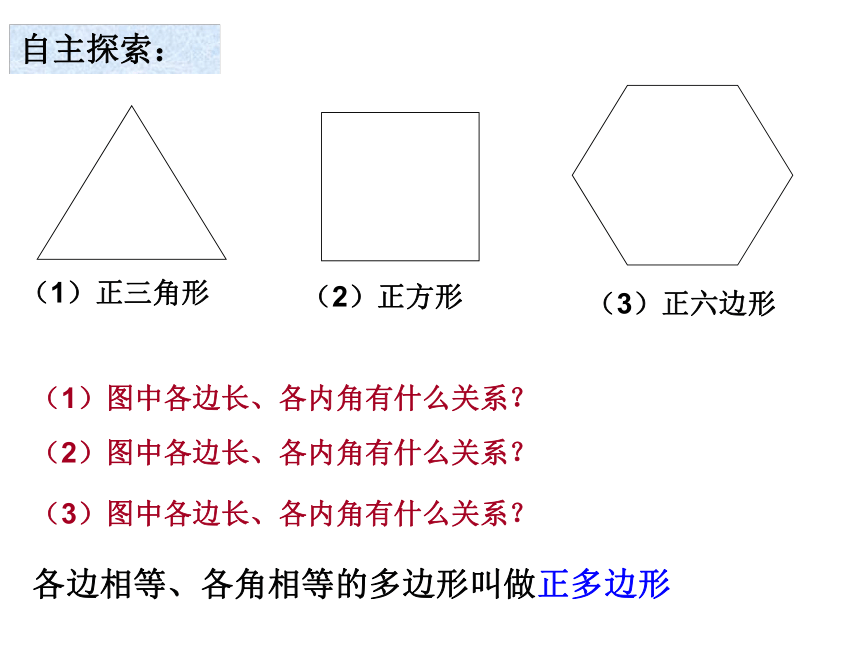
课件20张PPT。人人都参与到数学活动中，相信你能在参与过程中体验到快乐！ 5.1多边形(3)自主探索：（1）正三角形 （2）正方形 （3）正六边形 （1）图中各边长、各内角有什么关系？ （2）图中各边长、各内角有什么关系？ （3）图中各边长、各内角有什么关系？ 各边相等、各角相等的多边形叫做正多边形各边相等、各角相等的多边形叫做正多边形问题1:指出上图各是什么几何图形？问题2：求(1)图中的内角和？各个内角的度数？ （1） （2） （3） 你能求出（2）（3）图形各内角的度数吗？问题3：正五边形、正七边形、正八边形都是轴对称图形吗？
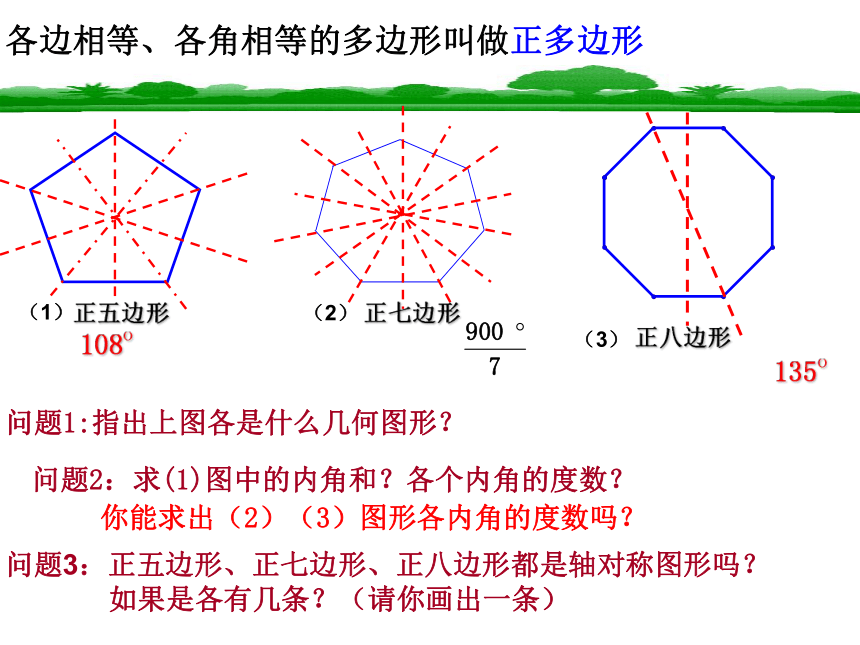
如果是各有几条？（请你画出一条）正五边形正七边形正八边形108o135o这些图案都是由哪些基本的平面图形构成的？ 这些图形拼成一个平面图案有什么共同特征 ？ ①②③④象这种既无缝隙又不重叠的铺法，我们称为 平面的镶嵌 合作学习 按要求操作，并逐步填写好“表格” （1）用若干个正三角形在桌面上尝试镶嵌平面
（2）用若干个正方形在桌面上尝试镶嵌平面
（3）用若干个正五边形在桌面上尝试镶嵌平面
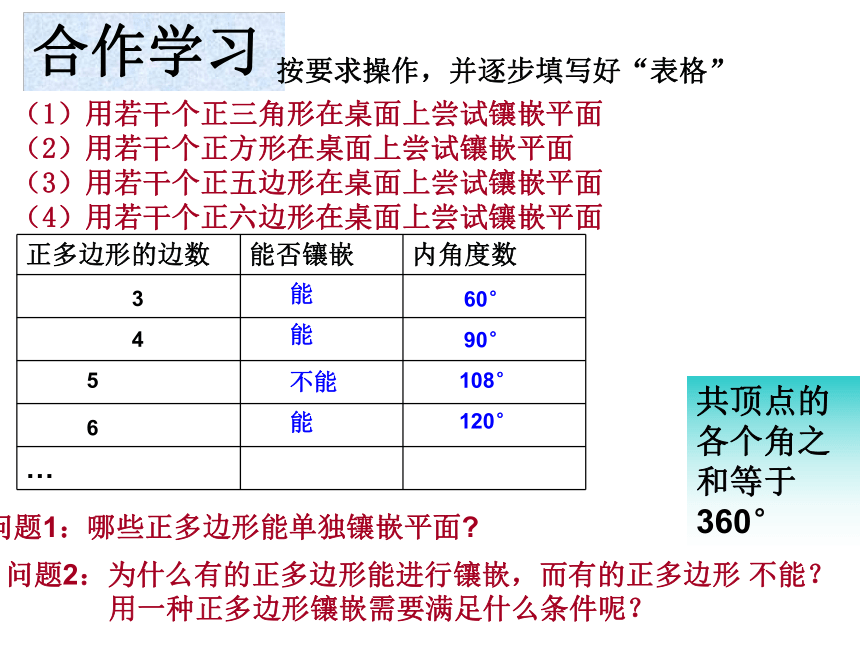
（4）用若干个正六边形在桌面上尝试镶嵌平面问题1：哪些正多边形能单独镶嵌平面? 问题2：为什么有的正多边形能进行镶嵌，而有的正多边形 不能？
用一种正多边形镶嵌需要满足什么条件呢？ 共顶点的
各个角之
和等于
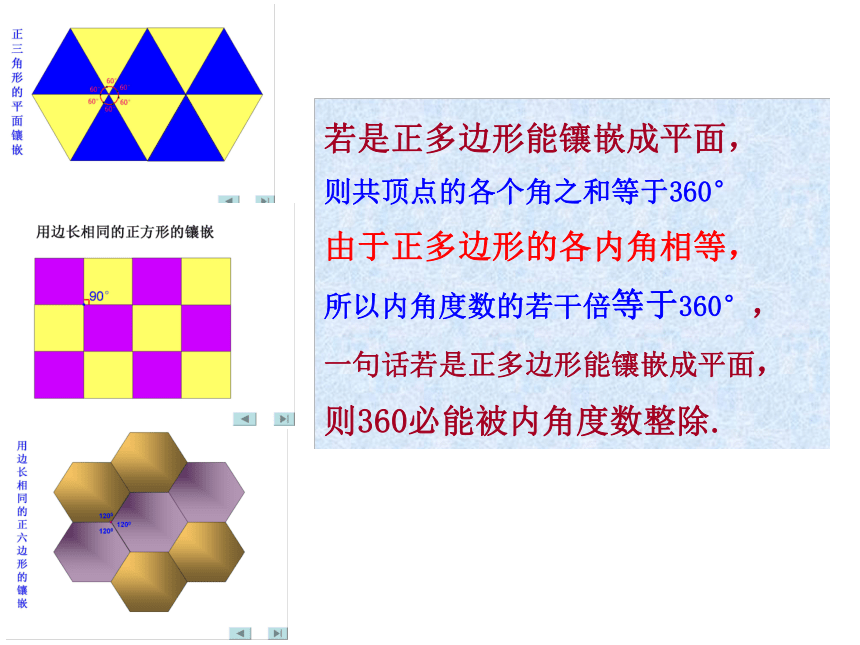
360° 3456能60°能不能能90°108°120°若是正多边形能镶嵌成平面，
则共顶点的各个角之和等于360°
由于正多边形的各内角相等，
所以内角度数的若干倍等于360°，
一句话若是正多边形能镶嵌成平面，
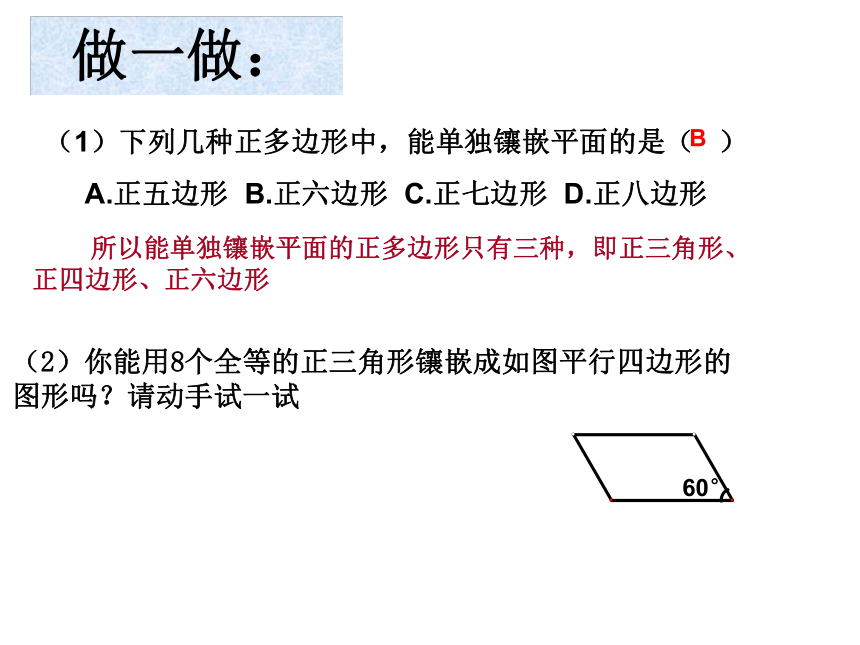
则360必能被内角度数整除.做一做： （1）下列几种正多边形中，能单独镶嵌平面的是（ ）
A.正五边形 B.正六边形 C.正七边形 D.正八边形 所以能单独镶嵌平面的正多边形只有三种，即正三角形、
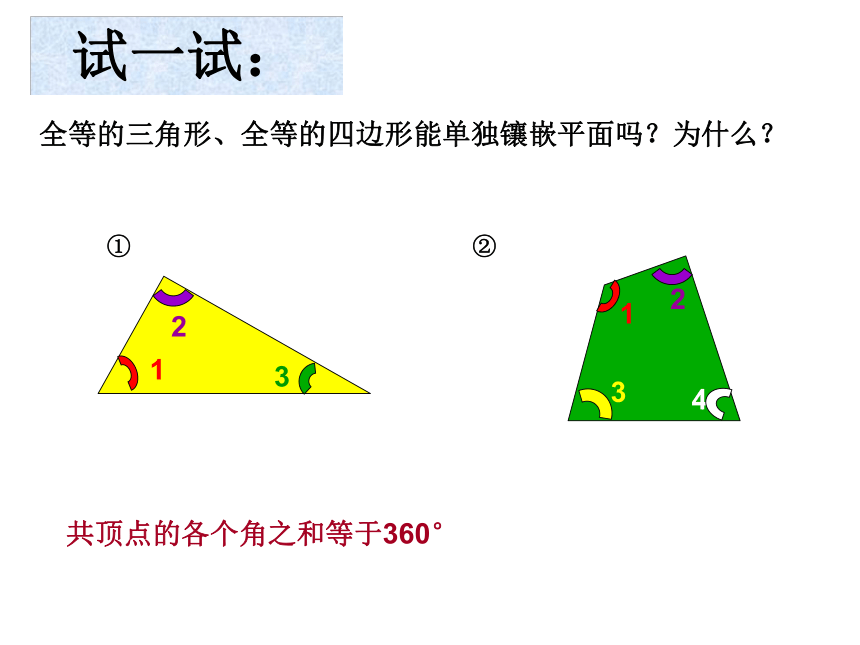
正四边形、正六边形B试一试： 全等的三角形、全等的四边形能单独镶嵌平面吗？为什么？ ①②共顶点的各个角之和等于360°想一想： 上述两图案是用多种正多边形镶嵌平面，你能说出其中的数学原理吗？(1)拼接在同一个点的各个角的和恰好等于360°(周角)； (2)相邻的多边形有公共边．试一试： 用边长相等的正方形和正八边形能镶嵌平面吗？并说明其中的数学原理.13501350900本节课你学到什么？小结各边相等、各角相等的多边形叫做正多边形各边相等、各角相等象这种既无缝隙又不重叠的铺法，我们称为平面的镶嵌 若是正多边形能镶嵌成平面，则共顶点的各个角之和等于360°( 若是多种多边形能镶嵌成平面，还须满足相邻的多边形有公共边）思考:(1)三边都相等的三角形是正三角形吗?(2)四边都相等的四边形是正方形吗?(3)四个角都相等的四边形是正方形吗?是不是不是作业：
课本P101 作业题 2、3、4必做
　 作业本
　 预习下一节课正三角形的平面镶嵌用边长相同的正方形的镶嵌90°用边长相同的正五边形镶嵌？用边长相同的正六边形的镶嵌 形状、大小完全相同的任意 三角形可以镶嵌平面吗？ 形状、大小完全相同的任意四边形 可以镶嵌平面吗？