5.1多边形(1)[下学期]

课件23张PPT。 多 边 形东山中学　　余爱玉 二人一小组用若干个正五边形的纸片摆一摆,拼一拼,正五多边形能拼成无缝隙的平面图形吗？你能说明其中的原因吗？
实践出真知 请同学们回忆:
①三角形的定义 ；
②三角形的表示方法;
③三角形的内角和、外角和
　分别等于多少度？ 由三条线段首尾顺次连结组成的图形叫做三角形。
记作△ABC 三角形的内角和： ∠A+∠B+∠C=180°
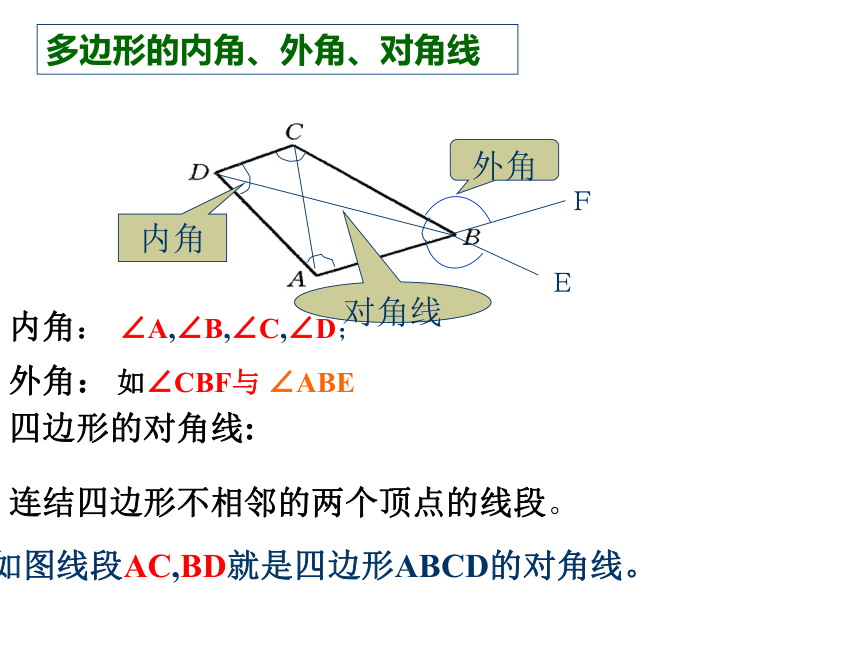
123外角和:∠ 1＋∠ 2+ ∠3 =360 °温故而知新多边形的内角、外角、对角线内角外角对角线内角： ∠A,∠B,∠C,∠D；
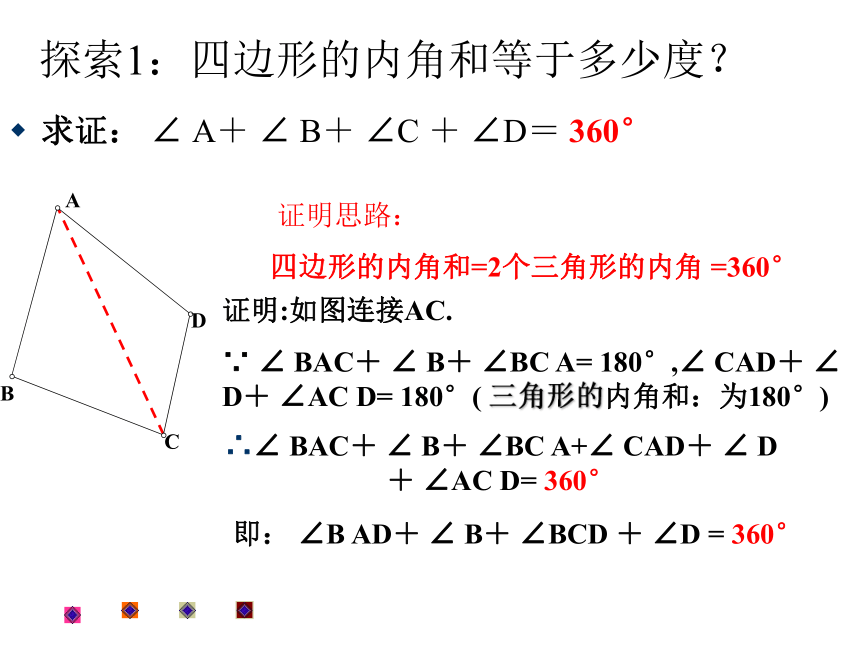
外角： 如∠CBF与 ∠ABE连结四边形不相邻的两个顶点的线段。四边形的对角线:ＦＥ如图线段AC,BD就是四边形ABCD的对角线。探索1：四边形的内角和等于多少度？求证： ∠ A＋ ∠ B＋ ∠C ＋ ∠D＝ 360° 证明思路：
四边形的内角和=2个三角形的内角 =360°证明:如图连接AC.
∵ ∠ BAC＋ ∠ B＋ ∠BC A= 180°,∠ CAD＋ ∠ D＋ ∠AC D= 180°( 三角形的内角和：为180°)
∴∠ BAC＋ ∠ B＋ ∠BC A+∠ CAD＋ ∠ D＋ ∠AC D= 360°即： ∠B AD＋ ∠ B＋ ∠BCD ＋ ∠D = 360° 证明思路：
四边形的内角和=4个三角形的内角和－1个周角
=4×180°－360° =360°探索方法2：求证： ∠ A＋ ∠ B＋ ∠C ＋ ∠D＝ 360°
证明:如图连接AC，ＢＤ相交与点O.
∵ ∠ BAＯ＋ ∠Ａ BＯ＋ ∠BＯ A= 180°,∠ ＯAD＋ ∠ＡＯ D＋ ∠ODＡ= 180°, ∠ ＯBC＋ ∠ BCＯ＋ ∠CＯ B= 180°,∠ CＯD＋ ∠CDＯ ＋ ∠DOC= 180° ( 三角形的内角和为180°)
∴ ∠DAB＋ ∠AB C＋ ∠BCD ＋ ∠CAD= ∠ BAＯ＋ ∠Ａ BＯ＋ ∠BＯ A+∠ ＯAD＋ ∠ＡＯ D＋ ∠ODＡ+ ∠ ＯBC＋ ∠ BCＯ＋ ∠CＯ B+∠ CＯD＋ ∠CDＯ ＋ ∠DOC= 4×180°－360° =360°
即： ∠DAB＋ ∠ABC ＋ ∠BCD ＋ ∠CDA = 360°探索方法3: 证求四边形的内角和等于360度 证明思路：
四边形的内角和=4个三角形的内角和－1个周角
=4×180°－360° =360°探索方法4：求证四边形的内角和为360度 证明思路：
四边形的内角和=3个三角形的内角和－1个平角
=3×180°－180° =360°。这是利用了四边形内角和定理:解开迷惑四边形的内角和=360°学以致用为了美化校园，我校准备再建造一个四边形的花坛(如图所示)设计如下：①如果将花坛设计成的四个内角都相等,那么这四个角都为 度
② 如果设计成∠A , ∠B ,∠C ,∠D的度数之比为1:2:3:4,则 ∠A = B _____
∠C = ∠D= .③若我班某同学绕着这新建花坛散步,原先站在C处,面朝D.他沿着CD方向转到下一条DA时身体转过的角是哪一个角？在图上标出.
④他走一圈回到C处,使面仍朝D.问:这个同学总共旋转了多少度?
⑤结论:∠ 1＋∠ 2+ ∠3 +∠4 = 360°
12349072°36°108°144°已知：如图，∠1 ,∠ 2,∠3 ,∠4
是四边形的四个外角。
求证：∠ 1＋∠ 2+ ∠3 +∠4 =360°求证:四边形的外角和等于360度解: ∵∠ 1+∠α =∠2+ ∠β= ∠3+∠γ= ∠ 4+∠δ= 180°
∴ ∠ 1+∠α +∠2+ ∠β+ ∠3+∠γ+ ∠ 4+∠δ =4× 180°= 720°
即: (∠ 1+∠2 +∠ 3 + ∠4)+ (∠α +∠ β + ∠ γ +∠δ) = 720°
∵ ∠α +∠ β + ∠ γ +∠δ=360°(根据四边形的内角和是360°)
∴ ∠1 +∠ 2 + ∠ 3 +∠4 = 720°－ 360°= 360°
推论: 四边形的外角和等于360° 把你的猜想、观察变成结论并整理出来！如果将花坛设计成三角形或五边形,(如图) .这个同学还是用同样的方式走转一圈,转过角度总和为多少?包含了什么数学规律?
课堂练习:1.如图：求∠β的度数解： ∠β的外角为（180°- ∠β）
∵ （180°- ∠β）+30 °+110 ° +85 ° =360 °
（四边形的外角和等于360 °）
∴ ∠β =45 °2. 已知：在四边形ABCD中,∠A＝∠C,∠B＝∠D，求∠A+∠B的度数． 3. 如图4.6-1,一块钉板上水平方向和垂直方向相邻两钉距离都是一个单位,橡皮筋构成一个四边形,那么它的面积为 ( )
A. 5.5 B. 6
C. 6.5 D. 7.5180°B
2．在四边形的四个内角中，锐角最多有几个?直角最多有几个?钝角最多有几个??3431．如图4－15，在四边形ABCD
AB⊥BC,AB=4,BC=3,CD=12,AD=13 ??????????????????????????? 求四边形ABCD的面积
?????????????????????????? 拓展知识5.小结四边形的内角和等于360°，外角和也等于360°.
通过与三角形的类比，得到四边形了有关概念.
把四边形的问题转化成三角形问题来求，数学常用的化归思想.作业作业本(一)
思考题:如果限于用一种 多边形镶嵌,哪几种正多边形能镶嵌一个平面图形
?感谢老师们，同学们！已知：如图,求∠A +∠B +∠C +∠D +∠E+ ∠F 的度数.解： 设DE，BC交于点O 连结BE
∵∠ C+∠D+∠COD= ∠OBE+∠BEO+∠EOB= 180°
且∠COD= ∠EOB
∴ ∠ C+∠D = ∠OBE+∠BEO
∴∠ A+ ∠ABC + ∠ C + ∠D + ∠DEF+ ∠ F
= ∠ A + ∠ABC + ∠OBE+∠BEO + ∠DEF+∠ F
= ∠ A+∠ABE + ∠BEF +∠ F =360°

挑战知识